以下分割线包含的内容转自大佬的博客:http://blog.csdn.net/magicnumber/article/details/43201063 感谢大佬让我转载
自己写的总结在最下面,建议按顺序看。
/**************************分割线************************/
看了一下具体数学的1.2章,整理了一下关于一个平面被分割的部分多少的问题
先考虑第一个小问题:
一个平面能被n条直线最多分成多少个部分?
假设用L来表示答案,那么有
最优的分法可以考虑是:
1. 没有两条直线互相平行
2. 没有三线共点
也就是说,如果现在有一个n条线的最优情况,我要新加第n+1条线,让他顺次穿过前n条线,即穿过了n+1个部分,即增加了n+1个部分(穿过了一个部分就可以把这个部分分成两半)
所以,初始情况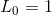
一个式子有两种长相,一种是递推式,一种是闭形式(不一定存在哟,有的也可能很复杂很复杂,例:斐波那契数列),闭形式说白了就是要求F(n)然后把n套进去就能得出函数的值,递推式就是要求F(n)就需要知道F(k) (k<n) 的值,这里可能需要一个k或者若干个k,或者更丧心病狂的可能需要知道F(0)到F(n-1)之间的所有值(Catalan数的最显而易见的那个递推式就是这样)
所以上头的是递推式
闭形式好搞,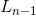
。。。。
发现L0=1诶,而后面则是一个1到n的和。
小高斯告诉我们,
因此,
如果用V字型的折线分割平面
假设用V表示最多分割的平面数量,则有
可以把V的两条射线反向延长,得到的就是2条交叉的线,如果我们就这样放着的话,相当于
但是,因为是V型的,所以两条反向延长线去掉之后,都会把三个部分合成一个部分,所以,对于每一个V,反向延长线去掉之后,平面分割的部分数目就要减去2,而总共有n个V型的线,所以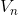
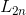
综上
也就是
Z字型的线分割平面的问题
对于一个Z,先当作三条线相交,但是很不幸,有一对平行线,所以分割的平面少了1,然后还有两个反向延长线需要去掉,分隔平面少了4,所以一条Z相比L3少了5个平面,因此:
如果是M字形的线分割平面结果呢(M的两个脚也是平行的)?
三对线没有交叉,因此少了3,三个角的反向延长线去掉了,又少了6。
推广一下,
如果F(n,m)表示n个折了m次的线最多能把平面分成的部分数,那么F(n,m)为多少呢?(例如M型的就是折了三次,有三个角,其中第一段和最后一段平行,其他段互不共线)
首先,折了m次的线就是由m+1条直线组成,因此就会有
对线,其中m对线有交点,因此不相交的直线数目有
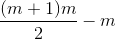
然后由于有m个角,每个角损失了2个部分,因此损失2m个部分。
综上
/************************分割线********************/
大佬的讲解比较清楚,但是对于M型切割以及最后总结的公式,我不是很理解,所以我自己又尝试着推导了一下。用另外一种方式来解释,
是否正确没法判定,但至少和上面已经推出来的通项公式一致………,如果你有兴趣可以往下看,欢迎提出问题并且与我讨论,如果没有可以直接略过。
首先你需要知道 L(n)=(n*n+n)/2+1;
L(n)代表n条直线最多分割平面的块数
Y(X)代表将X型图形的所有线段、射线延长后分割平面的个数
B(X)代表不延长线段平面被X型图形分割的块数,比如一个V型折线分割平面为2部分,一个W型,M型,Z型都是将平面分割成了两部分。
对于V型切割
只有一个V的时候,平面分成了两部分B(V)=2。然后将V的两条射线延长,那么平面被分成了4块,Y(V)=4
然后对于L(2)=4 因为将V的两条线延长之后等价于2条直线分割平面。此时V(n)=L(2n)-(Y(V)-B(V))*n-(L(2)-Y(V))*n=L(2n)-4n-0=L(2n)-4n; 后面L(2)-Y(V)考虑图形中出现互相平行的线段\射线的情况,显然V型 不存在平行的情况,所以减去0。
对于Z型切割
只有一个Z的时候,平面被分成两部分,B(Z)=2.然后将Z的两条射线一条线段双向延长,显然,平面被分成了6部分。Y(Z)=6
而L(3)=7 ,因为将Z的3条线段延长后等价于3条直线分割平面。所以Z(n)=L(3n)-(Y(Z)-B(Z))*n-(L(3)-Y(Z))*n=L(3n)-4n-n=L(3n)-5n
对于M型切割
只有一个M的时候,平面被分成两部分,B(M)=2,然后将M的四条线段双向延长,画出来,发现平面被分成了10个部分,Y(M)=10;
而L(4)=10,因为将M的4条线段延长后等价于4条直线分割平面,所以M(n)=L(4n)-(Y(M)-B(M))*n-(L(4)-Y(M))*n=L(4n)-8*n-n=L(4n)-9n;
对于W型切割
我们推出来和M型的公式是一样的。如果和你想的不一样,或者你有更好的想法,欢迎与我讨论,因为我从网上没找到W型切割的通项公式。











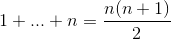
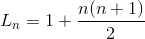
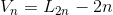
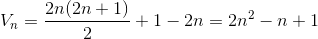
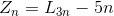
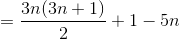
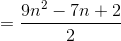
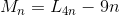
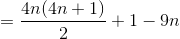

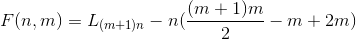
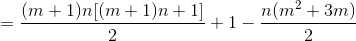
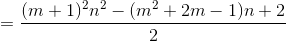
















 398
398

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








