初级算法梳理-决策树学习

决策树算法梳理

1.信息论基础（熵 联合熵 条件熵 信息增益 基尼不纯度）

补充点：自信息

某一件事情发生时所带来的信息量的多少，信息量便是可以从一件事情发生后可以得到信息。如果一件比较小概率的事件发生了，并且实际观察到了（观察结果），则获取的信息量将比较大，相反，如果一件概率非常大，并且也获得了观察结果，但是它的自信息相比前者就比较小。

​ $$I_{pi}=-lo{g}_{pi}$$

熵

定义

是随机变量不确定度的度量，在信息世界中，熵越高，则能传输越多信息，相反则越少。
如果压缩是无损的，即通过解压缩可以百分之百地恢复初始的消息内容，那么压缩后的消息携带的信息和未压缩的原始消息是一样的多。而压缩后的消息可以通过较少的比特传递，因此压缩消息的每个比特能携带更多的信息，也就是说压缩信息的熵更加高。熵更高意味着比较难于预测压缩消息携带的信息，原因在于压缩消息里面没有冗余，即每个比特的消息携带了一个比特的信息。香农的信息理论揭示了，任何无损压缩技术不可能让一比特的消息携带超过一比特的信息。消息的熵乘以消息的长度决定了消息可以携带多少信息。[Wikipedia]
香农的信息理论同时揭示了，任何无损压缩技术不可能缩短任何消息。根据鸽笼原理，如果有一些消息变短，则至少有一条消息变长。在实际使用中，由于我们通常只关注于压缩特定的某一类消息，所以这通常不是问题。例如英语文档和随机文字，数字照片和噪音，都是不同类型的。所以如果一个压缩算法会将某些不太可能出现的，或者非目标类型的消息变得更大，通常是无关紧要的。但是，在我们的日常使用中，如果去压缩已经压缩过的数据，仍会出现问题。[Wikipedia]

计算

设X是一个离散型随机变量，取值空间为y,则概率密度函数为

​ $P(x)=P_{\gamma }(X=x),x\in y$ 。

将P（x）以$P_X(x)$代替，由此，P(x)和P(y)指两个不同的随机变量，

实际上分别表示两个不同的概率密度函数$P_X(x)$ 和 $P_Y(y)$ .

一个离散型的随机变量X的熵$H(X)$ 定义为：

$H(X)=-{\sum }_{x\in x}logp(x)$

Wikipedia上面的一个例子：
如果有一枚理想的硬币，其出现正面和反面的机会相等，则抛硬币事件的熵等于其能够达到的最大值。我们无法知道下一个硬币抛掷的结果是什么，因此每一次抛硬币都是不可预测的。因此，使用一枚正常硬币进行若干次抛掷，这个事件的熵是一比特，因为结果不外乎两个——正面或者反面，可以表示为0, 1编码，而且两个结果彼此之间相互独立。若进行n次独立实验，则熵为n，因为可以用长度为n的比特流表示。但是如果一枚硬币的两面完全相同，那个这个系列抛硬币事件的熵等于零，因为结果能被准确预测。现实世界里，我们收集到的数据的熵介于上面两种情况之间。

另一个稍微复杂的例子是假设一个随机变量X，取三种可能值$x_1$, $x_2$，$x_3$，概率分别为$\frac{1}{2}$, $\frac{1}{4}$, $\frac{1}{4}$，那么编码平均比特长度是：
$$\frac{1}{2}\ast 1+\frac{1}{4}\ast 2+\frac{1}{4}\ast 2=\frac{3}{2}$$
其熵为3/2。

因此熵实际是对随机变量的比特量和顺次发生概率相乘再总和的数学期望

联合熵

定义

是一集变量不确定性的衡量手段。

两个变量 和Y定义为：
$$H(X,Y)=-\sum \sum P(x,y)lo{g}_2[P(x,y)]$$
其中 x 和 y 是 X 和 Y的特定值, 相应地,P(x,y) 是这些值一起出现的联合概率,
若 P(x,y)=0 为0，则 $P(x,y){\log }_2[P(x,y)]$ 定义为0。

对于两个以上的变量 $X_1,...,X_n$ ，该式的一般形式为：
$$H(X_1,...,X_n)=-\sum \sum P(x_1,...,x_n)lo{g}_2[P(x_1,...,x_n)]$$
其中 $x_1,...,x_n$ 是 $X_1,...,X_n$ 的特定值，

相应地,$P(x_1,...,x_n)$ 是这些变量同时出现的概率，

若$P(x_1,...,x_n)=0$为0，则 $P(x_1,...x_n)lo{g}_2[P(x_1,...,x_n)]$被定义为0.

性质

• 大于每个独立的熵

  一集变量的联合熵大于或等于这集变量中任一个的独立熵.

• 少于或等于独立熵的和

  一集变量的联合熵少于或等于这集变量的独立熵之和。这是次可加性的一个例子。该不等式有且只有在X和Y均为统计独立的时候相等。

条件熵

定义

描述了在已知第二个随机变量 X 的值的前提下，随机变量 Y 的信息熵还有多少。同其它的信息熵一样，条件熵也用Sh、nat、Hart等信息单位表示。
基于 X 条件的 Y 的信息熵，用$\mathrm{H}(Y|X)$ 表示。

如果$\mathrm{H}(Y|X=x)$ 为变数Y 在变数X 取特定值 x 条件下的熵，那么 $\mathrm{H}(Y|X)$ 就是 $\mathrm{H}(Y|X=x)$ 在X 取遍所有可能的 x 后取平均的结果。

给定随机变量 X 与 Y，定义域分别为 $\mathcal{X}$ 与 $\mathcal{Y}$，在给定X 条件下 Y 的条件熵定义为：

注意： 可以理解，对于确定的 c>0，表达式 0 log 0 和 0 log (c/0) 应被认作等于零。

当且仅当 Y 的值完全由 X 确定时，$\mathrm{H}(Y|X)=0$。相反，当且仅当 Y 和 X 为独立随机变数时$\mathrm{H}(Y|X)=\mathrm{H}(Y)$。

条件熵的贝叶斯规则：

证明.

$H(Y|X)=H(X,Y)-H(X)$ and $H(X|Y)=H(Y,X)-H(Y)$

对称性意味着 $H(X,Y)=H(Y,X)$。

将两式相减即为贝叶斯规则。

信息增益

定义：

又被称为KL散度（Kullback–Leibler divergence，简称KLD）

KL散度是两个概率分布P和Q差别的非对称性的度量。 KL散度是用来 度量使用基于Q的编码来编码来自P的样本平均所需的额外的位元数。 典型情况下，P表示数据的真实分布，Q表示数据的理论分布，模型分布，或P的近似分布。
对于离散随机变量，其概率分布P 和 Q的KL散度可按下式定义为

等价于

即按概率P求得的P和Q的对数商的平均值。KL散度仅当概率P和Q各自总和均为1，且对于任何i皆满足$Q(i)>0$及$P(i)>0$时，才有定义。式中出现$0\ln 0$的情况，其值按0处理。
对于连续随机变量，其概率分布P和Q可按积分方式定义为:

其中p和q分别表示分布P和Q的密度。

更一般的，若P和Q为集合X的概率测度，且P关于Q绝对连续，则从P到Q的KL散度定义为

其中，假定右侧的表达形式存在，则$\frac{\mathrm{d}Q}{\mathrm{d}P}$为Q关于P的R–N导数

相应的，若P关于Q绝对连续，则

即为P关于Q的相对熵。

性质

相对熵的值为非负数：

由吉布斯不等式可知，当且仅当P = Q时DKL(P||Q)为零。

尽管从直觉上KL散度是个度量或距离函数, 但是它实际上并不是一个真正的度量或距离。因为KL散度不具有对称性：从分布P到Q的距离通常并不等于从Q到P的距离。

与其他量的联系

自信息和KL散度

互信息和KL散度

信息熵和KL散度

条件熵和KL散度

交叉熵和KL散度

基尼不纯度

在CART算法中, 基尼不纯度表示一个随机选中的样本在子集中被分错的可能性。

基尼不纯度为这个样本被选中的概率乘以它被分错的概率。当一个节点中所有样本都是一个类时，基尼不纯度为零。

假设y的可能取值为J个类别，另$i\in 1,2,...,J$，$p_i$表示被标定为第i类的概率，则基尼不纯度的计算为：

2.决策树的不同分类算法（ID3算法、C4.5、CART分类树）的原理及应用场景

ID3算法

​ ID3由Ross Quinlan在1986年提出。ID3决策树可以有多个分支，但是不能处理特征值为连续的情况。

​ 决策树是一种贪心算法，每次选取的分割数据的特征都是当前的最佳选择，并不关心是否达到最优。在ID3中，每次根据“最大信息熵增益”选取当前最佳的特征来分割数据，并按照该特征的所有取值来切分，也就是说如果一个特征有4种取值，数据将被切分4份，一旦按某特征切分后，该特征在之后的算法执行中，将不再起作用，所以有观点认为这种切分方式过于迅速。ID3算法十分简单，核心是根据“最大信息熵增益”原则选择划分当前数据集的最好特征，信息熵是信息论里面的概念，是信息的度量方式，不确定度越大或者说越混乱，熵就越大。在建立决策树的过程中，根据特征属性划分数据，使得原本“混乱”的数据的熵(混乱度)减少，按照不同特征划分数据熵减少的程度会不一样。在ID3中选择熵减少程度最大的特征来划分数据（贪心），也就是“最大信息熵增益”原则。

​ ID3算法可以归纳为以下几点：

• 使用所有没有使用的属性并计算与之相关的样本熵值

• 选取其中熵值最小的属性

• 生成包含该属性的节点

计算公式：

C4.5

​ C4.5是Ross Quinlan在1993年在ID3的基础上改进而提出的。

​ C4.5算法与ID3算法一样使用了信息熵的概念，并和ID3一样通过学习数据来建立决策树。训练数据是已经分类的样本集合$S=s_1,s_2,...$。每个样本$s_i$, 由p维向量$x_{1,i},x_{2,i},...,x_{p,i}$组成，其中表示样本的属性值或者叫特征，当然也包括样本 $s_i$ 的类别。在树的每个节点上，C4.5选择数据的属性，该属性最有效地将其样本集划分为集中在一个类或另一个类中的子集。划分准则是归一化的信息增益，即熵的差。选择信息增益最大的属性进行决策，然后对划分后的子集进行递归处理。

计算公式：

CART分类树

​ CART（Classification and Regression tree）分类回归树由L.Breiman,J.Friedman,R.Olshen和C.Stone于1984年提出。

​ CART是一个独立于其他经典决策树算法的算法，所以导致CART相对来说较为复杂。因为它不仅仅可以作为分类树，还可以作为回归树。采用的是Gini指数（选Gini指数最小的特征s）作为分裂标准,同时它也是包含后剪枝操作。ID3算法和C4.5算法虽然在对训练样本集的学习中可以尽可能多地挖掘信息，但其生成的决策树分支较大，规模较大。为了简化决策树的规模，提高生成决策树的效率，就出现了根据GINI系数来选择测试属性的决策树算法CART。

​ CART分类树预测分类离散型数据，采用基尼指数选择最优特征，同时决定该特征的最优二值切分点。分类过程中，假设有K个类，样本点属于第k个类的概率为Pk，则概率分布的基尼指数定义为

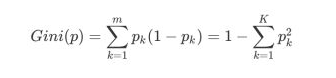
根据基尼指数定义，可以得到样本集合D的基尼指数，其中Ck表示数据集D中属于第k类的样本子集。

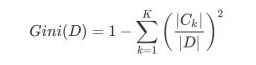
如果数据集D根据特征A在某一取值a上进行分割，得到D1,D2两部分后，那么在特征A下集合D的基尼系数如下所示。其中基尼系数Gini(D)表示集合D的不确定性，基尼系数Gini(D,A)表示A=a分割后集合D的不确定性。基尼指数越大，样本集合的不确定性越大。

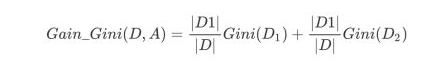
对于属性A，分别计算任意属性值将数据集划分为两部分之后的Gain_Gini，选取其中的最小值，作为属性A得到的最优二分方案。然后对于训练集S，计算所有属性的最优二分方案，选取其中的最小值，作为样本及S的最优二分方案。

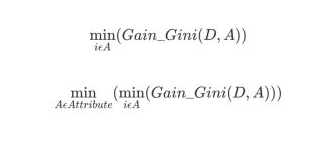
3. 回归树原理 & 决策树防止过拟合手段

回归树是建立在决策树上的，主要的差别是每个节点上不再是预测一个类别而是预测一个值。

决策树在处理回归任务时，也很容易过拟合，可以同一下几点进行控制：

1. 控制树的深度，也就是树有多少层。
2. 一个节点能被继续拆分出子节点所需要的包含最少的样本个数。
3. 最底层节点所需要包含的最少样本个数。
4. 进行减枝
5. 使用随机生成树

5. 模型评估

使用CART算法分裂的训练集使用最小化MSE，则相应的成本函数便是：

$$J(k,t_k)=\frac{m_{left}}{m}MS{E}_{left}+\frac{m_{right}}{m}MS{E}_{right}$$,

其中，
$$\begin{gathered} MS{E}_{node}=\sum _{i\in node}(y_{node}-y^i{)}^2 \\ {y}_{node}=\frac{1}{m_{node}}\sum _{i\in node}^i \end{gathered}$$

6. sklearn参数详解，Python绘制决策树

使用Python调用sklearn DecisionTreeRegressor

import numpy as np
import matplotlib.pyplot as plt
from sklearn.tree import DecisionTreeRegressor

# Create a random dataset
rng = np.random.RandomState(1)
X = np.sort(200 * rng.rand(100, 1) - 100, axis=0)
y = np.array([np.pi * np.sin(X).ravel(), np.pi * np.cos(X).ravel()]).T
y[::5, :] += (0.5 - rng.rand(20, 2))

# Fit regression model
regr_1 = DecisionTreeRegressor(max_depth=2)
regr_2 = DecisionTreeRegressor(max_depth=5)
regr_3 = DecisionTreeRegressor(max_depth=8)
regr_1.fit(X, y)
regr_2.fit(X, y)
regr_3.fit(X, y)

# Predict
X_test = np.arange(-100.0, 100.0, 0.01)[:, np.newaxis]
y_1 = regr_1.predict(X_test)
y_2 = regr_2.predict(X_test)
y_3 = regr_3.predict(X_test)

# Plot the results
plt.figure()
s = 25
plt.scatter(y[:, 0], y[:, 1], c="navy", s=s,
            edgecolor="black", label="data")
plt.scatter(y_1[:, 0], y_1[:, 1], c="cornflowerblue", s=s,
            edgecolor="black", label="max_depth=2")
plt.scatter(y_2[:, 0], y_2[:, 1], c="red", s=s,
            edgecolor="black", label="max_depth=5")
plt.scatter(y_3[:, 0], y_3[:, 1], c="orange", s=s,
            edgecolor="black", label="max_depth=8")
plt.xlim([-6, 6])
plt.ylim([-6, 6])
plt.xlabel("target 1")
plt.ylabel("target 2")
plt.title("Multi-output Decision Tree Regression")
plt.legend(loc="best")
plt.show()

结果如下图：

sklearn DecisionTreeRegresion部分参数说明

• criterion ： string，optional（default =“mse”）

  衡量分裂质量的功能。支持的标准是均方误差的“mse”，它等于作为特征选择标准的方差减少，并使用每个终端节点的平均值“friedman_mse”最小化L2损失，其使用弗里德曼的潜在改进得分的均方误差分裂，并且“mae”表示平均绝对误差，其使用每个终端节点的中值来最小化L1损失。

• splitter ： string，optional（default =“best”）

  用于在每个节点处选择拆分的策略。支持的策略是“最佳”选择最佳分割和“随机”选择最佳随机分割。

• max_depth ： int或None，可选（默认=无）

  树的最大深度。如果为None，则扩展节点直到所有叶子都是纯的或直到所有叶子包含少于min_samples_split样本。

• min_samples_split ： int，float，optional（default = 2）

  拆分内部节点所需的最小样本数：

  • 如果是int，则将min_samples_split视为最小数字。

  • 如果是float，则min_samples_split是一个分数， ceil（min_samples_split * n_samples）是每个分割的最小样本数。

• min_samples_leaf ： int，float，optional（default = 1）

  叶子节点所需的最小样本数。只有min_samples_leaf在每个左右分支中留下至少训练样本时，才会考虑任何深度的分裂点。这可能具有平滑模型的效果，尤其是在回归中。

  • 如果是int，则将min_samples_leaf视为最小数字。

  • 如果是float，则min_samples_leaf是一个分数， ceil（min_samples_leaf * n_samples）是每个节点的最小样本数。

• random_state ： int，RandomState实例或None，可选（默认=无）

如果是int，则random_state是随机数生成器使用的种子; 如果是RandomState实例，则random_state是随机数生成器; 如果没有，随机数生成器所使用的RandomState实例np.random。

• max_leaf_nodes ： int或None，可选（默认=无）

  max_leaf_nodes以最好的方式种树。最佳节点定义为杂质的相对减少。如果为None则无限数量的叶节点。

• min_impurity_split ： float，（默认值= 1e-7）

  树木生长早期停止的门槛。如果节点的杂质高于阈值，节点将分裂，否则它是叶子。

• presort ： bool，optional（默认值= False）

  是否预先分配数据以加快拟合中最佳分割的发现。对于大型数据集上的决策树的默认设置，将其设置为true可能会降低培训过程的速度。当使用较小的数据集或受限深度时，这可以加速训练。

参考

sklearn document

wikipiedia