上一次,我们简单整理了一些创建几何形体的节点用法,今天我们接着整理一些,几何形体的编辑方法。
一、坐标点的平移复制
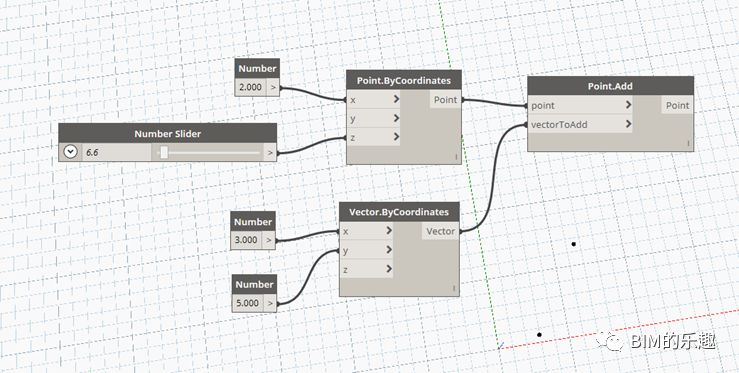
[Point.Add] 使用节点 “Vector.ByCoordinates” 生成一个向量,将该向量连接到 “Point.Add” 节点的输入端 “point”。另将被平移复制的坐标点作为输入项,连接到“point” 输入端,则将输入的坐标点按照向量的方向和长度平移复制。如图所示,输入坐标点为(2,5,0),输入向量为(3,5,0),平移复制后的坐标点为(5,10,0)。
二、几何形体的平移复制
[Geometry.Translate] 在 Dynamo 中,另一个常用的平移复制的节点是
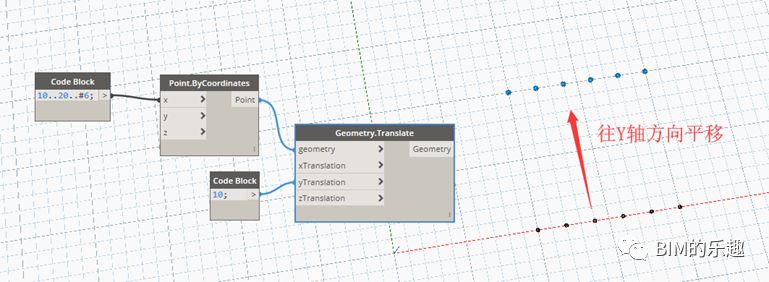
“Geometry.Translate”,适用于所有的几何形体,上例中坐标点的平移复制同样可以使用该节点实现。如下图,输入项分别输入 XYZ 三个方向上平移的坐标分量,即 0,10,0, 将坐标点向 Y 轴方向平移 10 个单位 长度。此节点同样适用于曲线、曲面实体等几何形体的平移复制。
三、几何形体的镜像复制
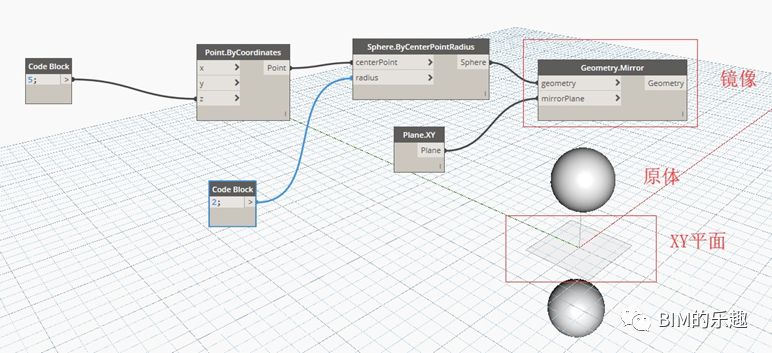
[Geometry.Mirror] 通过输入指定平面,将几何形体根据平面镜像复制。例子中,指定平面为 XY 平面,被镜像的几何形体是球心坐标为(0,0,5),半径为 2 的球体。
四、几何形体的旋转复制
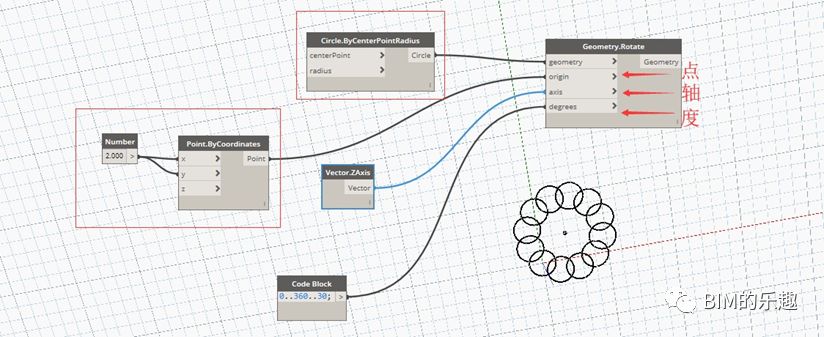
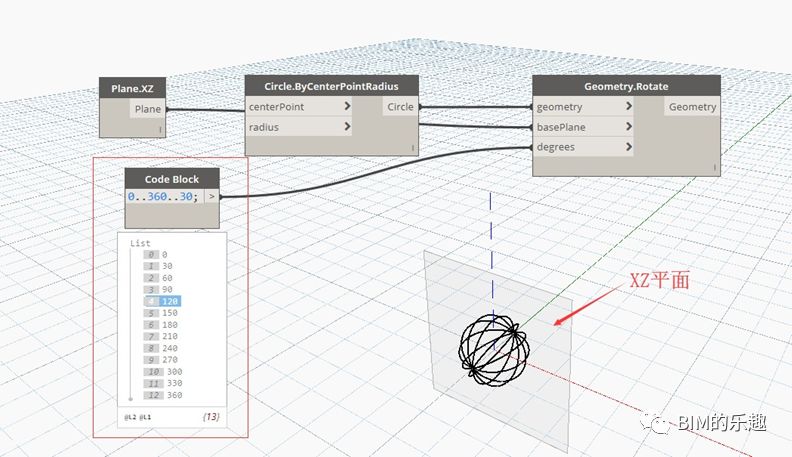
[Geometry.Rotate] “Geometry.Rotate”节点用于几何形体的旋转。输入项包括被旋转的几何形体、绕其旋转的基准坐标点、旋转轴向量、旋转角度。图例中,半径为 1 的圆形,绕基准坐标点 (2,2,0) 旋转,旋转轴为 (0,0,1) 向量,旋转角度为 “0,30,60,90…,360” 的角度列表。
[Geometry.Rotate] 还有另一种形式,输入端为被旋转的几何体、旋转基准面和旋转角度。圆形一 XZ 平面为基准面旋转,生成如图所示的旋转结果。
五、几何形体的缩放
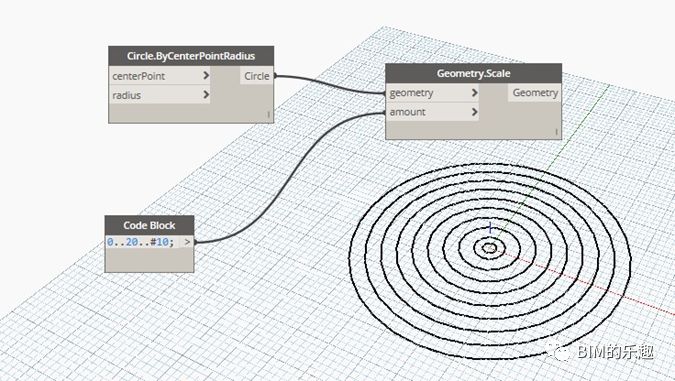
[Geometry.Scale] 几何形体的等比例缩放,可以使用节点 “Geometry.Scale”。 输入项为等比例缩放的几何形体以及缩放因子。缩放因子可以是一个数值,也可以是一个数值表。
六、获取几何形体间的距离
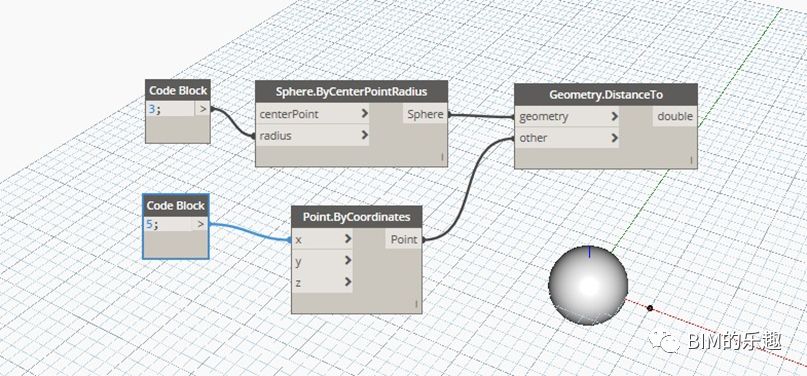
[Geometry.DistanceTo] 该节点用于获取几何形体间的空间位置关系,测量两个几何形体间的最短距离。例如图中球心为 (0,0,0), 半径为 3 的球体,距离坐标点(5,0,0) 的距离为 2。测量的是球体表面距坐标点最短的距离。
七、几何形体的拆分
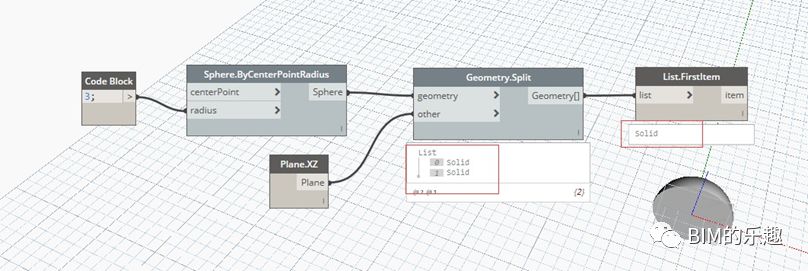
[Geometry.Split] 使用任意几何形体(曲线、曲面和实体)对目标几何 形体进行拆分。前提是两个几何形体需要有相交区域。例子中,目标几何形体是球心 (0,0,0), 半径为 3 的球体,作为拆分工具的几何形体是 XZ 平面。则可将球体分割为两个半球,注意“Geometry.Split” 的运算结果是两个 “Solid”。使用“List.FirstItem” 将其中一个 “Solid” 选取出来,隐藏上游节点,则在三维预览视图中,仅显示其中一个半球。
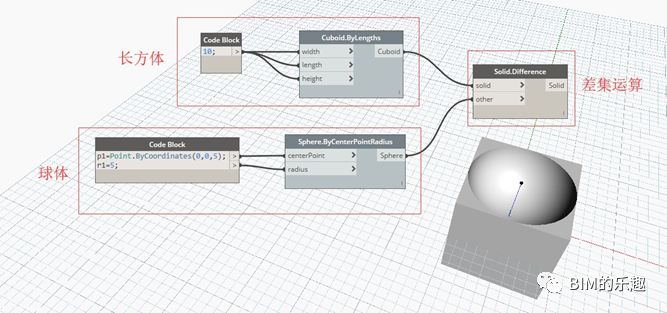
八、几何形体的差集、并基与交集
创建一个长宽高为 10 的立方体,中心坐标为 (0,0,0)。在创建一个球心坐标为 (0,0,5), 半径为 5 的球体。两个几何形体有相交区域,以此为例,进行差集、并集和交集的运算。
[Solid.Difference] 两个几何形体求差集的运算。
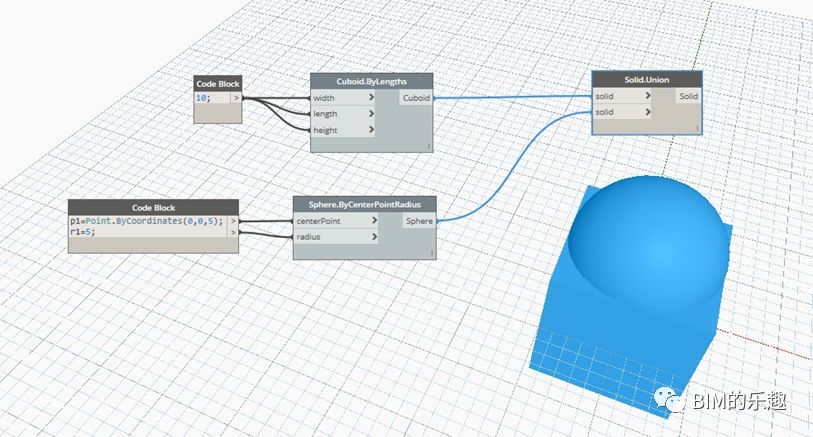
[Solid.Union] 两个几何形体求并集的运算。三维视图中显示的是求并集运算后的结果,为一个单一的 “Solid”。
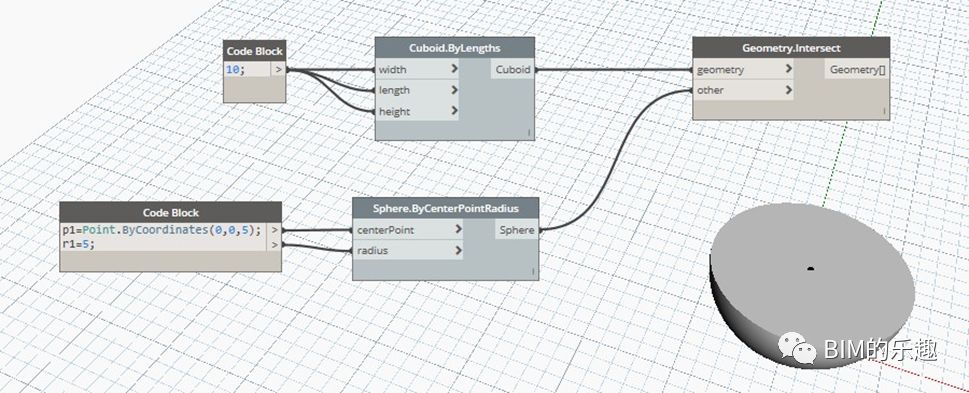
[Geometry.Intersect] 两个几何形体求交集的运算。
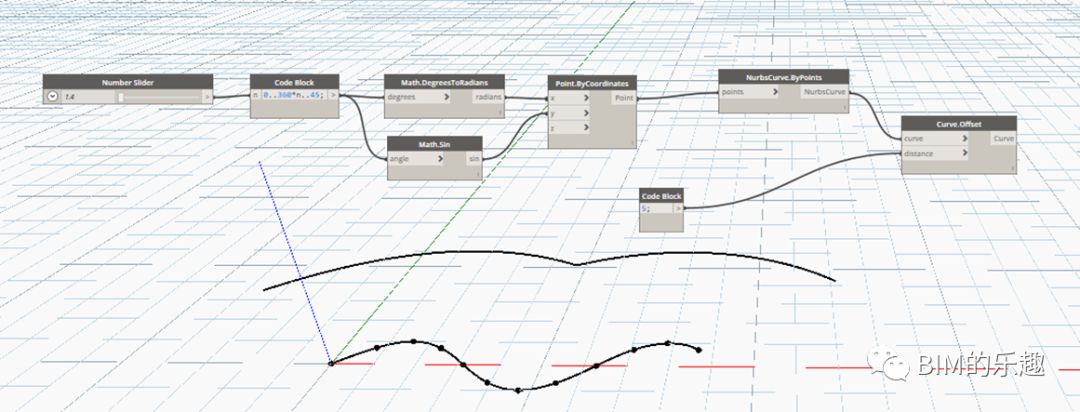
九、曲线的偏移
[Curve.Offset]通过输入偏移距离,将曲线根据默认方向偏移复制。
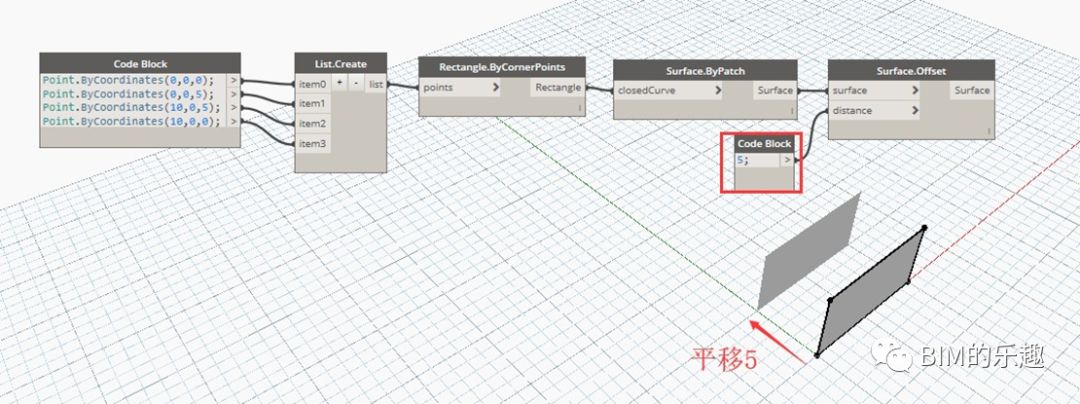
十、曲面的偏移
Surface.Offset]通过输入曲面和偏移距离,将曲面朝曲面法向量方向偏移复制。
最近比较忙,今天就简单整理这十条吧,其实最近关于 Dynamo 的中文资料,网上越来越多了,我只是简单整理一些,方便大家学习!

























 2300
2300

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










