ISCC 2017 部分解题记录 By Assassin

Basic 50 Wheel Cipher

加密表：
1:  < ZWAXJGDLUBVIQHKYPNTCRMOSFE <
2:  < KPBELNACZDTRXMJQOYHGVSFUWI <
3:  < BDMAIZVRNSJUWFHTEQGYXPLOCK <
4:  < RPLNDVHGFCUKTEBSXQYIZMJWAO <
5:  < IHFRLABEUOTSGJVDKCPMNZQWXY <
6:  < AMKGHIWPNYCJBFZDRUSLOQXVET <
7:  < GWTHSPYBXIZULVKMRAFDCEONJQ <
8:  < NOZUTWDCVRJLXKISEFAPMYGHBQ <
9:  < XPLTDSRFHENYVUBMCQWAOIKZGJ <
10: < UDNAJFBOWTGVRSCZQKELMXYIHP <
11： < MNBVCXZQWERTPOIUYALSKDJFHG <
12： < LVNCMXZPQOWEIURYTASBKJDFHG <
13： < JZQAWSXCDERFVBGTYHNUMKILOP <

密钥为：2，3，7，5，13,12,9，1，8，10，4，11，6
密文为：NFQKSEVOQOFNP

直接google一下发现是什么二战时期的一个轮转加密，直接按照他得规律写脚本就好了

#coding:utf-8
import re
sss='''
1:  < ZWAXJGDLUBVIQHKYPNTCRMOSFE <
2:  < KPBELNACZDTRXMJQOYHGVSFUWI <
3:  < BDMAIZVRNSJUWFHTEQGYXPLOCK <
4:  < RPLNDVHGFCUKTEBSXQYIZMJWAO <
5:  < IHFRLABEUOTSGJVDKCPMNZQWXY <
6:  < AMKGHIWPNYCJBFZDRUSLOQXVET <
7:  < GWTHSPYBXIZULVKMRAFDCEONJQ <
8:  < NOZUTWDCVRJLXKISEFAPMYGHBQ <
9:  < XPLTDSRFHENYVUBMCQWAOIKZGJ <
10: < UDNAJFBOWTGVRSCZQKELMXYIHP <
11  < MNBVCXZQWERTPOIUYALSKDJFHG <
12  < LVNCMXZPQOWEIURYTASBKJDFHG <
13  < JZQAWSXCDERFVBGTYHNUMKILOP <
'''
#密钥为：2，3，7，5，13,12,9，1，8，10，4，11，6
#密文为：NFQKSEVOQOFNP
m="NFQKSEVOQOFNP"
content=re.findall(r'< (.*?) <',sss,re.S)
iv=[2,3,7,5,13,12,9,1,8,10,4,11,6]
vvv=[]
ans=""
for i in range(13):
    index=content[iv[i]-1].index(m[i])
    vvv.append(index)

for i in range(0,26):
    flag=""
    for j in range(13):
        flag+=content[iv[j]-1][(vvv[j]+i)%26]
    print flag

发现flag

Basic 100 说我作弊，需要证据

本题目是一个 RandomsCTF上的原题，是一个比较好的RSA+数字验证的题目！下面讲一下解题的步骤
首先我们拿到了一个数据包，然后观察一下TCP流可以找到有许多base64加密的数据流

然后我们首先base64解密一下观察一下

SEQ = 13; DATA = 0x3b04b26a0adada2f67326bb0c5d6L; SIG = 0x2e5ab24f9dc21df406a87de0b3b4L;
SEQ = 0; DATA = 0x7492f4ec9001202dcb569df468b4L; SIG = 0xc9107666b1cc040a4fc2e89e3e7L;
SEQ = 5; DATA = 0x94d97e04f52c2d6f42f9aacbf0b5L; SIG = 0x1e3b6d4eaf11582e85ead4bf90a9L;
SEQ = 4; DATA = 0x2c29150f1e311ef09bc9f06735acL; SIG = 0x1665fb2da761c4de89f27ac80cbL;
SEQ = 18; DATA = 0x181901c059de3b0f2d4840ab3aebL; SIG = 0x1b8bdf9468f81ce33a0da2a8bfbeL;
SEQ = 2; DATA = 0x8a03676745df01e16745145dd212L; SIG = 0x1378c25048c19853b6817eb9363aL;
SEQ = 20; DATA = 0x674880905956979ce49af33433L; SIG = 0x198901d5373ea225cc5c0db66987L;
SEQ = 0; DATA = 0x633282273f9cf7e5a44fcbe1787bL; SIG = 0x2b15275412244442d9ee60fc91aeL;
SEQ = 28; DATA = 0x19688f112a61169c9090a4f9918dL; SIG = 0x1448ac6eee2b2e91a0a6241e590eL;
...

然后我们观察，可以通过查找资料发现，这个就是RSA+数字签名

然后我们已经知道了Alice和Bob的公钥对

X老师怀疑一些调皮的学生在一次自动化计算机测试中作弊，他使用抓包工具捕获到了Alice和Bob的通信流量。狡猾的Alice和Bob同学好像使用某些加密方式隐藏通信内容，使得X老师无法破解它，也许你有办法帮助X老师。X老师知道Alice的RSA密钥为(n, e) = (0x53a121a11e36d7a84dde3f5d73cf, 0x10001) (192.168.0.13)?,Bob的RSA密钥为(n, e) =(0x99122e61dc7bede74711185598c7, 0x10001) (192.168.0.37)

然后我们有一个大数分解的神奇网站
大数分解

然后我们可以分别分解n得到Alice和Bob运算中的p和q

Alice's p and q are 38456719616722997 and 44106885765559411.
Bob's p and q are 49662237675630289 and 62515288803124247.

然后我们可以通过 扩展欧几里得算法得到d，好多人用的python gmpy库，但是windows下太难装了，而我们直到p和q后根据RSA算法知道

$$N=（p-1）*（q-1）$$
$$ed==1 mod((p-1)*(q-1))$$
简单讲一下扩展欧几里得，我们看一组简单的运算

扩展欧几里得算法求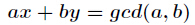的是方程的解。原理如下
设a>b，当时b==0，gcd(a,b)==a，此时x=1,y=0，否则设

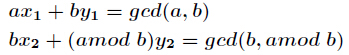
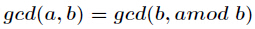
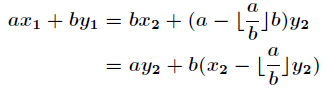
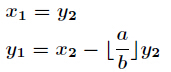
由于，所以进一步得到

然后我们就可以写脚本了，exgcd函数如下

def exgcd(a,b):
    if b==0:
        return 1,0
    tempx,tempy=exgcd(b,a%b)
    tmp = tempx
    x=tempy
    y = tmp - (a / b) * tempy
    return x,y

然后我们就知道两个人的d了

然后我们写一个RSA的类，记录两个人的不同变量内容