入门笔记+题集:SOSdp

2023大厂真题提交网址(含题解):

www.CodeFun2000.com（http://101.43.147.120/）

最近我们一直在将收集到的机试真题制作数据并搬运到自己的OJ上，供大家免费练习,体会真题难度。现在OJ已录入50+道2023年最新大厂真题，同时在不断的更新。同时，可以关注"塔子哥学算法"公众号获得每道题的题解。

1.介绍:

原文链接

1.1.SOSdp($Sumoversubsetsdp$)顾名思义，子集和dp。用来维护子集信息的。俗称高维前缀和.

1.2.最常见的形式：求解$dp(mask)={\sum }_{i\in mask}{a}_i$

注意：$i\in mask等价于i\&mask=i等价于i|mask=mask$

常见的解法是$O(3^n)$枚举子集。使用sosdp可以加速到$O(n\ast 2^n)$.

1.3.做法:$S(mask,i)$代表集合$mask$只有前$i$位不同的子集$a_i$和.

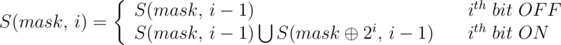
合法性:

无非就是证明计数不重不漏呗。对于任意一个$i$的子集$j$.它们一定有一段前缀是相同的。所以$i$的子集的计数可以分解成$logi$个阶段去做:$i$的全子集 = 前$logi$个位不同的子集和=上面的转移。(这个就有点像前缀和优化了)

1.4.编码:

//iterative version
for(int mask = 0; mask < (1<<N); ++mask){
   
	dp[mask][-1] = A[mask];	//handle base case separately (leaf states)
	for(int i = 0;i < N; ++i){
   
		if(mask & (1<<i))
			dp[mask][i] = dp[mask][i-1] + dp[mask^(1<<i)][i-1];
		else
			dp[mask][i] = dp[mask][i-1];
	}
	F[mask] = dp[mask][N-1];
}
//memory optimized, super easy to code.
for(int i = 0; i<(1<<N); ++i)
	F[i] = A[i];
for(int i = 0;i < N; ++i) for(int mask = 0; mask < (1<<N); ++mask){
   
	if(mask & (1<<i))
		F[mask] += F[mask^(1<<i)];
}

解释：两种不同的dp顺序。第一种是正常的状压dp的顺序：从小集合往大集合dp。
第二种是从低位到高位去dp。

2.应用:

基础定义比较好理解，但是它的应用非常广泛，技巧多。需要刷比较多的题才能加深对$sosdp$的理解。

2.1.ARC100E

题目地址

题目大意:

给你$2^n$个数。问你每个$k\in [0,2^n-1]$，求解 max ⁡ i   o r   j ≤ k { a i + a j } \max_{i\ or\ j\leq k}\{a_i+a_j\} maxi or j≤k​{ ai​+aj​}.
$n\le 18$

题目思路:
这个题需要比较奇妙的转换:

1.$i|j\le k$比较难求解，将其变成$i|j=g\le k$,所以每个$i|j=g$，求前缀最大值即可。

2.但是上面还是不好处理。我们直接转换成子集的形式:$(i|j)\in k$.那么也就是$i\in k\&\&j\in k$.那么显然对每个$k$,求其下标$i$为$k$的子集的最大值和次大值.最后前缀最大值即可.

代码:

pii a[maxn];
void trans (int i , int j)
{
   
    int mx = max (a[i].fi , a[j].fi);
    int se = max(min(a[i].fi , a[j].fi) , max (a[i].se , a[j].se));
    a[i].fi = mx;
    a[i].se = se;
}
int main()
{
   
    ios::sync_with_stdio(false);
    int n; cin >> n;
    int s = 1 << n;
    for (int i = 0 ; i < s ; i++){
   
        int x; cin >> x;
        a[i] = {
   x , -inf};
    }
    for (int j = 0 ; j < n ; j++){
   
        for (int i = 0 ; i < s ; i++){
   
            if (i >> j & 1) trans(i , i ^ (1 << j));
        }
    }
    int ans = -inf;
    for (int i = 1 ; i < s ; i++){
   
        ans = max(ans , a[i].fi + a[i].se);
        cout << ans << endl;
    }
    return 0;
}

2.2:CF1208

题目地址

题目大意:
给一个长度为$n$的序列，求 m a x { a i ∣ ( a j & a k ) } , 1 ≤ i < j < k ≤ n max\{a_i|(a_j\&a_k)\},1 \leq i <j<k \leq n max{ ai​∣(aj​&ak​)},1≤i<j<k≤n
n ≤ 1 e 6 n \leq 1e6