AOE图和关键路径的求解

AOE网和关键路径

本文算是相对知识密度较大的文章，建议看的时候慢一点，并在迷惑的地方搜索其他文章。

---

AOE网和AOV网

一些概念

拓扑结构：拓扑本是地理上的概念，指只考虑物体间的位置关系而不考虑它们的形状和大小。拓扑结构就是某些东西之间有位置关系。

拓扑排序：给一个局部有序的拓扑结构排序。如：吃饭->睡觉，睡觉->打豆豆。在拓扑排序后则变成：吃饭->睡觉->打豆豆，这样的拓扑序列。

Activity On Vertex：用顶点表示活动，用弧表示活动间的优先关系的有向图。

活动：如吃饭睡觉打豆豆等，在企鹅的一天这个工程中都是活动。

事件：类似于里程碑，标志着之前的某些活动都已经完成。如：顶点5标志活动a4,a5已完成，a7,a8可以开始了。（a7的先序活动为a4或a5）

Activity On Edge：是一个带权的有向无环图，其中，顶点表示事件（Event),弧表示活动，权表示活动持续的时间。 入度为零的顶点成为源点，出度为零的顶点称为汇点。

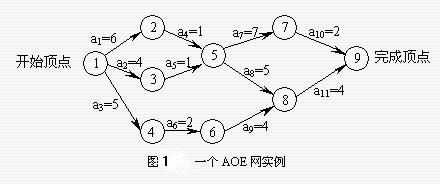
AOE网可以求解：

1. 完成整个工期的时间。
2. 为缩短工期，应加快哪些活动。

关系：AOV网常用来拓扑排序，AOE网用来规划工程计划。

关键路径

从源点到汇点具有最大长度的路径，关键路径上的所以活动都称作关键活动。

关键活动序列具有最长的总工期并决定了整个项目的最短完成时间，任何元素的延迟将直接影响项目的预期完成时间。

关键路径相关量

其中，v：vertex，e：early，l：late。

以下可以在‘最’字前加上“可以”，便于理解。如：事件可以的最早发生事件。

1. 事件的最早发生时间：ve[k]

从源点开始到顶点Vk的最大路径长度（即权值的和）。

这个长度决定了从顶点Vk发出的活动能够开工的最早时间。

如：顶点5标志着活动a4、a5已完成，则以a4、a5为前序活动的a7、a8则可以开始进行。

求解：

ve[0] = 0;

ve[k] = max{ve[j] + len<Vj, Vk>}

即：从上个顶点Vj开始，ve[k]加上从该顶点到Vk顶点路径的最大值。

2. 事件的最迟发生时间：vl[k]

指在不推迟整个工期的前提下，事件Vk允许的最晚发生事件。

vl[n] = ve[n]

vl[k] = min{vl[j] - len<Vk, Vj>}

即：从它的下一个顶点Vj开始，vl[j]减去该顶点到Vk顶点路径的最小值。

注：上述两个相关量求解时总是为最大或最小值，是因为某个顶点的前一个顶点或后一个顶点可能有多个。我们所说的“Vk的前一个顶点”指的是与Vk有弧，且弧头指向Vk的顶点。

3. 活动的最早开始时间：e[i]

字面意思。

e[i] = ve[k]

即：e[i]等于该弧的弧尾所在顶点的ve[k]的值。

4. 活动的最迟开始时间：l[i]

l[i] = vl[j] - len<Vk, Vj>

即：该弧的弧头所在顶点对应的vl[k]减去该弧的权值。

然后就可计算各个活动的时间余量（l[k] - e[k] ），时间余量为0者为关键活动。

工程规划

在求出关键路径和各个活动的时间余量后，便可做出规划：

若要保证工程完成工期较短，则关键活动必须要马不停蹄的完成。

而时间余量不为零的那些活动，则可以拖延相应的时间。

关键活动。

工程规划

在求出关键路径和各个活动的时间余量后，便可做出规划：

若要保证工程完成工期较短，则关键活动必须要马不停蹄的完成。

而时间余量不为零的那些活动，则可以拖延相应的时间。

也可通过上面求得的关键路径相关量，计算安排每个活动开始的时间范围，和整个工程的最短工期。