【机器学习】LDA（线性判别分析）或fisher判别分析

内容目录：
一、LDA/fisher判别分析
二、LDA判别分析与PCA对比

一、fisher判别分析

1.首先在模式识别课程上学习的是fisher判别，LDA概念是看川大同学写的500问接触的，两者是一样的东西。
2推荐：深度学习500问 github链接形式是问答形式，初学者概念补充。挺有意思的，饭后阅读物！
3fisher分类标准：类间的距离越大且类内的距离越小。
4fisher目的：寻找到一条直线，当把所有数据点投影到直线上之后，尽可能的分开不同类别的训练数据。如下图所示，右边的图的直线投影后无法将其分开，而左边的直线投影后可以很好的将两类分开，分界面定义为，两类在投影后的各自均值点求平均点O，并过此点做投影直线的中垂线。

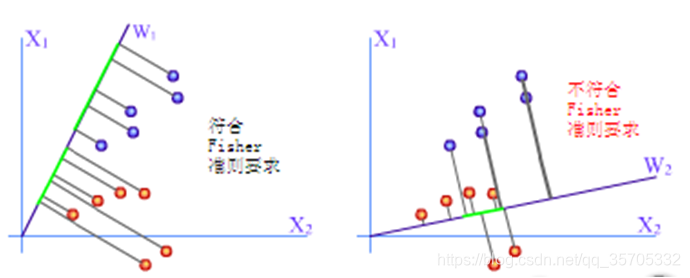
5分界面所示：

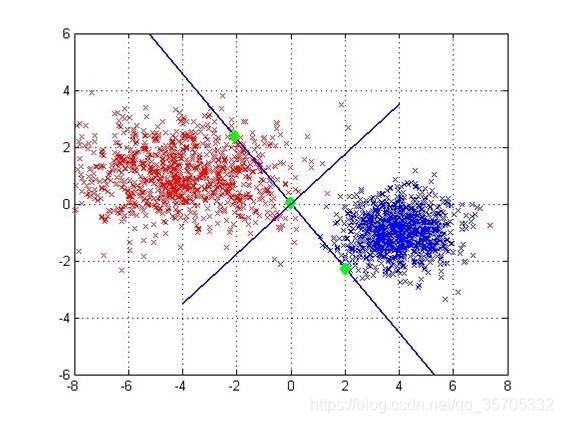
6推导过程：
根据分类原则，类内距离尽可能小，类间距离尽可能大，所以定义了代价函数=类间方差矩阵除以类内方差矩阵。即目标要最大化代价函数。

基本概念数学表达式：

举例：一维两类

w的确定（最佳法线向量，投影直线）
4-30推导到4-32时：是把Sb公式4-19带入了，且（m1-m2）'w（矩阵维度：1dd1=11）为常量就省去了，因为W是作为方向参考，乘上一个常数因子不影响方向。

二、fisher判别分析与PCA比较：

1共同点：两者都是降维处理。
2降维维度：pca可以达到任意维度，可以只取矩阵分解后特征值最大的一个特征向量，也可以取其他；fisher投影降维只能降到K-1维（类别数-1，两类之间判断是或不是？？？这个点怎么理解？？？），也比常用数据的属性特征的维数少很多。
3fisher可做分类器：