【Programming Languages And Lambda calculi】4.7~4.8 关于Lambda演算的一些事实 范式 历史 第四章完

4.7 关于Lambda演算的一些事实

什么时候一个表达式是完全还原的？几乎所有的表达式可以用 →_n^α 将变量名重命名来约化，所以 →_n^α 不能被算在定义内。因此，一个完全还原的表达式是无法再由 →_n^β →_n^η 约化的表达式。

概念：

• 如果一个表达式无法再由 →_n^β →_n^η 约化，则它被称为范式。

• M 有范式 N 如果 M =_n N 并且 N 是范式。

范式的作用与Lambda演算表达式的结果一样。如果一个表达式有范式，则它有且仅有唯一的范式（可能通过很多不同的约化得到）。更准确地说， →_n^α 重命名取模只能得到一个范式。

定理 4.2 [范式] : 如果 L =_n M，L =_n M，并且 M 和 N都是范式，则 M =_α N

如往常一样， =_α 为由 α 兼容闭合生成的等价关系。定理 4.2 易由 Church-Rosser 性质证明：

***定理 4.3 [ =_n 代表 Church-Rosser 关系]***: 如果 M =_n N，则存在一个L’ 使得 M →→_n L’ 且 N →→_n L’

至于 =_r ，这个定理的证明取决于 →→_n 的棱形性质。

定理 4.4 [ →→_n 代表棱形性质] : 如果 L →→_n M 且 L →→_n N，则存在一个表达式 L’ 使 M →→_n L’ 且 N →→_n L’

单步关系 →_n 并不满足棱形性质，甚至不满足轻微的扭曲关系，比如 →_r 的类-棱形性质。原因是→_n^β 可以重复可约表达式。比如：

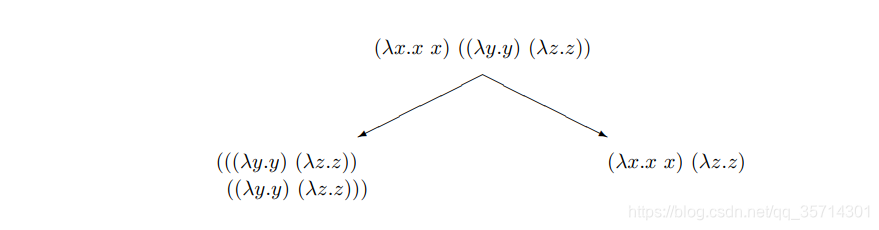
对于上述的两个约化表达式，没有一个单步关系能够将他们约化为同一个表达式。在下一节我们会知道，解决这个问题的方式是围绕子关系式定义一个平行约化的概念，这样左边的两个((λy.y) (λz.z))子表达式可以被同时约化。现在，我们暂时不会尝试证明定理 4.4。在下一章我们会演示关联语言的棱形性质。

不像 B 中的关系式，每一个表达式的结果不是 f 就是 t，并不是每一个Lambda表达式都有范式。比如，Ω 不存在范式：

即使一个表达式存在范式，也有可能存在一个无限约化顺序使其永远无法变成范式，例如：

因此，定理 4.2 只保证最多只存在一个范式，但是我们目前为止并没有找到它的方法。直观上来说，上述这个无限约化的问题