常用的信号处理函数Scipy之滤波器

常用的信号处理库scipy

在 Python 中，我们可以利用 SciPy 库中的函数来创建低通滤波器。SciPy 是 Scientific Python 的缩写，是一个用于提供执行信号处理、优化和统计的函数的库。该库还使用下面的 NumPy 库。

滤波器

考虑scipy库：Scipy

数字滤波器中最基础的莫过于FIR和IIR这两个类型，首先了解一个概念，什么是有限脉冲响应FIR和无线脉冲响应IIR滤波器？
具体可参考：
FIR/IIR滤波器
FIR滤波器与IIR滤波器的具体区别

FIR滤波器：
FIR是从滑动平均方法牵引出来的基于卷积的一种滤波方法，可以说FIR天然是具有直观的“数字处理”的特性。

设计一个频域滤波器（将想要保留的频率段赋值为1，其他频率段赋值为0），将其与含噪声信号的频谱在频域上相乘，再将乘积做傅里叶逆变换，即可实现滤波，这种滤波器叫频域滤波器。

将上述的理论浓缩成一个表达式，表示FIR滤波器：

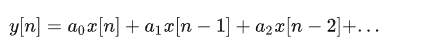
上式中的x代表待滤波数据，y代表输出数据；系数a0、a1、a2…就是滤波器的冲激响应系数。所以在FIR滤波器中，每一时刻的输出取决于之前的有限个输入，因此就是“有限冲激响应”。

IIR滤波器：
IIR方法和物理世界有着对应的联系，或者说它是对“模拟滤波器”的数字表达。
IIR 滤波器设计的基本方法：先设计一个合适的模拟滤波器（模拟原型滤波器），然后利用复值映射把模拟滤波器变换成数字滤波器。
常用的模拟原值滤波器有很多种，比如：
■ 巴特沃斯滤波器通带最平坦，阻带下降慢。
■ 切比雪夫滤波器通带等纹波，阻带下降较快。
■ 贝塞尔滤波器通带等纹波，阻带下降慢。也就是说幅频特性的选频特性最差。但是，贝塞尔滤波器具有最佳的线性相位特性。
■ 椭圆滤波器在通带等纹波（阻带平坦或等纹波），阻带下降最快。

IIR滤波器的表达式为：

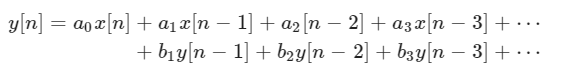
上式通过将输入信号的值乘以“a”系数，将先前从输出信号计算的值乘以“b”系数，并将乘积相加，可以找到输出信号中的每个点，上式称为递归公式。由于本步骤的输出会作为下一步骤的输入，无限递归下去，所以一个时刻的影响就是无限的，也就是“无限冲激响应”。

总结：
两种滤波器都是数字滤波器。根据冲激响应的不同，将数字滤波器分为有限冲激响应（FIR）滤波器和无限冲激响应（IIR）滤波器。对于FIR滤波器，冲激响应在有限时间内衰减为零，其输出仅取决于当前和过去的输入信号值。对于IIR滤波器，冲激响应理论上应会无限持续，其输出不仅取决于当前和过去的输入信号值，也取决于过去的信号输出值。FIR滤波器可以提供线性相位响应，而IIR滤波器则不能。

scipy.signal.firwin

该函数用来计算滤波器的系数。

scipy.signal.firwin(numtaps, cutoff, width=None, window='hamming', pass_zero=True, scale=True, nyq=None, fs=None)

输入参数：
1.numtaps： int
滤波器的长度(系数的数量，即滤波器阶数 + 1)。如果通带包括奈奎斯特频率，则 numtaps 必须是奇数。

• 滤波器将具有线性相位；如果 numtaps 为奇数则为 Type I，如果 numtaps 为偶数则为 Type II。
• II 型滤波器在奈奎斯特频率处始终具有零响应，因此如果使用 numtaps 偶数调用 firwin 并且具有右端位于奈奎斯特频率的通带，则会引发 ValueError 异常。

2.cutoff： 浮点数或一维 数组
滤波器的截止频率(以与 fs 相同的单位表示)或一组截止频率。在后一种情况下，截止频率应该是正的，并且在 0 和 fs/2 之间单调增加。值 0 和 fs/2 不得包含在截止值中。

3.width： 浮点数或无，可选
如果 width 不是 None，则假定它是用于 Kaiser FIR 滤波器设计的过渡区域的近似宽度(以与 fs 相同的单位表示)。在这种情况下，window 参数将被忽略。

4.window： 字符串或字符串和参数值的元组，可选
想要使用的窗口。有关窗口和所需参数的列表，请参见scipy.signal.get_window。

5.pass_zero： {真，假，‘bandpass’, ‘lowpass’, ‘highpass’, ‘bandstop’}，可选
如果为 True，则频率 0(即 “DC gain”)处的增益为 1。如果为 False，则直流增益为 0。也可以是所需滤波器类型的字符串参数(相当于 IIR 设计函数中的 btype )。

6.scale： 布尔型，可选
设置为 True 以缩放系数，以便频率响应在某个频率处完全一致。该频率是：

• 0 (DC) 如果第一个通带从 0 开始(即 pass_zero 为真)
• fs/2(奈奎斯特频率)，如果第一个通带以 fs/2 结束(即滤波器是单频带高通滤波器)；否则为第一通带中心

7.nyq： 浮点数，可选
已弃用。请改用fs。这是奈奎斯特频率。截止频率中的每个频率必须介于 0 和 nyq 之间。默认值为 1。

8.fs： 浮点数，可选
信号的采样频率。每个截止频率必须介于 0 和 fs/2 之间。默认值为 2。

输出返回
h： (numtaps,) ndarray
numtaps FIR 滤波器长度的系数。

ValueError
如果 cutoff 中的任何值小于或等于 0 或大于或等于fs/2，如果值在隔断不是严格单调递增的，或者如果小数点是偶数，但通带包括奈奎斯特频率。

一般和firwin连用的还有个lfilter

scipy.signal.lfilter

使用 IIR 或 FIR 滤波器沿 one-dimension 过滤数据。

scipy.signal.lfilter(b, a, x, axis=- 1, zi=None)

对数据序列x进行滤波。这适用于许多基本数据类型(包括对象类型)。该滤波器是标准差分方程的直接形式II的转置实现。

对于大多数滤波任务，函数sosfilt(和使用output='sos’的滤波器设计)应该优先于lfilter，因为second-order部分的数值问题较少。

描述该滤波器在z变换域中的有理传递函数为：

输入参数：
1. b: 类数组
一个一维序列的系数向量，方程的分子。

2. a: 类数组
一维序列系数向量，分母。如果a[0]不是1，那么a和b都由a[0]归一化。

3. x: 类数组
n维输入数组。

4. axis: int, 可选
用于线性滤波器的输入数组的轴。滤波器应用于沿此轴的每一个子数组。默认值为-1。

5. zi: 类数组, 可选
滤波器的延迟的初始条件。它是一个长度为max(len(a)， len(b)) - 1的向量(或n维输入的向量数组)。如果zi为None或未给出，则假定初始休眠。

输出返回
1. y: 类数组
数字滤波器的输出。

2. zf: 类数组，可选
如果zi为None，则不返回此值，否则，zf保存最终的滤波器延迟值。

举例：
一个高通滤波，去掉70Hz以下部分

fs = 16000
cutoff = 70
nyquist = fs // 2
norm_cutoff = cutoff / nyquist

fil = firwin(255, norm_cutoff, pass_zero=False)
# 255即系数个数，Pass_zero不写就是低通，False就是高通（f就一个值）或带通（f为多个值如[f1,f2]）
l = lfilter(fil, 1, x)
# 分子fil,分母1，

实现FIR滤波器：

from scipy.signal import firwin, lfilter

# 构建fir滤波器，设定采样频率为128Hz
firb = firwin(order,[low_cut, high_cut], fs = 128, window = 'Hamming')
fira = 1
# 滤波，firb代表分子，fira代表分母
ouput = lfilter(firb, fira, input)

实现IIR滤波器：

from scipy.signal import iirfilter, lfilter

# 构建iir滤波器
iirb, iira = iirfirwin(order,[low_cut, high_cut], fs = 128)
# 滤波，iirb代表分子，iira代表分母
ouput = lfilter(iirb, iira, input)

FIR是线性的，IIR是非线性的。它们共有的问题是需要巧妙的设计，尤其是对于非线性非平稳信号，需要高阶设计才能达到良好的效果。

scipy.signal.filtfilt

scipy.signal.filtfilt()函数可以方便快捷的实现常见的多种滤波功能。

filter_data=scipy.signal.filtfilt(b, a, x, axis=-1, padtype='odd', padlen=None, method='pad', irlen=None)

输入参数：
1.b: 滤波器的分子系数向量；
2.a: 滤波器的分母系数向量；
3.x: 要过滤的数据数组；
4.axis: 指定要过滤的数据数组x的轴；
5.padtype: 必须是“奇数”、“偶数”、“常数”或“无”。这决定了用于过滤器应用的填充信号的扩展类型。{‘odd’, ‘even’, ‘constant’, None}
**6.padlen：**在应用滤波器之前在轴两端延伸X的元素数目。此值必须小于要滤波元素个数- 1。（int型或None）
7.method： 确定处理信号边缘的方法。当method为“pad”时，填充信号；填充类型padtype和padlen决定，irlen被忽略。当method为“gust”时，使用古斯塔夫森方法，而忽略padtype和padlen。{“pad” ，“gust”}
8.irlen： 当method为“gust”时，irlen指定滤波器的脉冲响应的长度。如果irlen是None，则脉冲响应的任何部分都被忽略。对于长信号，指定irlen可以显著改善滤波器的性能。（int型或None）

实例：低通巴特沃斯滤波器

在 Python 中创建一个 Butterworth 低通滤波器，因为它具有最大平坦的频率，这意味着通带中没有波纹。这使其成为最流行和最常用的低通滤波器之一。

import numpy as np
from scipy.signal import butter, lfilter, freqz
import matplotlib.pyplot as plt


def butter_lowpass(cutoff, fs, order=5):
    nyq = 0.5 * fs
    normal_cutoff = cutoff / nyq
    b, a = butter(order, normal_cutoff, btype='low', analog=False)
    return b, a

def butter_lowpass_filter(data, cutoff, fs, order=5):
    b, a = butter_lowpass(cutoff, fs, order=order)
    y = lfilter(b, a, data)
    return y


# Setting standard filter requirements.
order = 6
fs = 30.0       
cutoff = 3.667  

b, a = butter_lowpass(cutoff, fs, order)

# Plotting the frequency response.
w, h = freqz(b, a, worN=8000)
plt.subplot(2, 1, 1)
plt.plot(0.5*fs*w/np.pi, np.abs(h), 'b')
plt.plot(cutoff, 0.5*np.sqrt(2), 'ko')
plt.axvline(cutoff, color='k')
plt.xlim(0, 0.5*fs)
plt.title("Lowpass Filter Frequency Response")
plt.xlabel('Frequency [Hz]')
plt.grid()


# Creating the data for filteration
T = 5.0         # value taken in seconds
n = int(T * fs) # indicates total samples
t = np.linspace(0, T, n, endpoint=False)

data = np.sin(1.2*2*np.pi*t) + 1.5*np.cos(9*2*np.pi*t) + 0.5*np.sin(12.0*2*np.pi*t)

# Filtering and plotting
y = butter_lowpass_filter(data, cutoff, fs, order)

plt.subplot(2, 1, 2)
plt.plot(t, data, 'b-', label='data')
plt.plot(t, y, 'g-', linewidth=2, label='filtered data')
plt.xlabel('Time [sec]')
plt.grid()
plt.legend()

plt.subplots_adjust(hspace=0.35)
plt.show()

还有一个例子：

import numpy as np
import matplotlib.pyplot as plt
from scipy import signal

# 定义滤波器的参数
n = 5  # 滤波器阶数
cut_off = 0.2  # 截止频率

# 生成低通滤波器的系数
b, a = signal.butter(n, cut_off, 'low')

# 产生随机信号，并添加噪声
t = np.linspace(0, 1, 1000, endpoint=False)
signal_in = np.sin(2 * np.pi * 10 * t) + np.sin(2 * np.pi * 20 * t) + np.sin(2 * np.pi * 50 * t)
noise = np.random.normal(0, 1, signal_in.shape)
signal_input = signal_in + noise

# 对产生的信号进行滤波
signal_output = signal.filtfilt(b, a, signal_input)

# 绘制原始信号和滤波后的信号的图像
plt.plot(t, signal_in, 'r-', linewidth=1, label='Original Signal')
plt.plot(t, signal_output, 'b-', linewidth=1, label='Filter Signal')
plt.legend(loc='best')
plt.show()

运行代码后，可以看到产生的随机信号中含有高频成分，经过低通滤波器滤波后，高频成分被滤除，得到了一个更加平滑的信号。

将cutoff = 0.05，则：

其他滤波器

Scipy信号处理包也提供了更多的滤波器。

中值滤波（Median Filter）：
中值滤波器通常应用于噪声明显非高斯或希望保留边缘的情况。中值滤波器的工作原理是对感兴趣点周围矩形区域内的所有数组像素值进行排序。此邻域像素值列表的样本中位数用作输出数组的值。样本中位数是邻域值排序列表中的中间数组值。如果邻域中有偶数个元素，则使用中间两个值的平均值作为中位数。用于N-D数组的通用中值过滤器是medfilt。一个专门的版本只适用于二维数组，名为medfilt2d。

y = scipy.signal.medfilt(volume, kernel_size=None)

• 输入：
  volume:n维输入数组。
  kernel_size:每个维度中值过滤器窗口的大小。kernel_size的元素应该是奇数。如果kernel_size是一个标量，则使用该标量作为每个维度的大小。每个维度的默认大小为3。
• 输出：
  与输入相同大小的数组。

阶滤波器（Order Filter）:
中值滤波器是阶滤波器的一个特例。为了计算特定像素处的输出，所有阶滤波器都使用该像素周围区域中的数组值。将这些数组值排序，然后选择其中一个作为输出值。对于中值滤波器，使用数组值列表的样本中位数作为输出。一般阶滤波器允许用户选择将哪个排序值用作输出。比如，可以选择列表中的最大值或者最小值。除了输入数组和区域掩码之外，阶滤波器还接受一个额外的参数，该参数指定相邻数组值排序列表中的哪个元素应该用作输出。执行订单筛选的命令是order_filter。

y = scipy.signal.order_filter(a, domain, rank)

• 输入：
  a:n维输入数组。
  domain:与A具有相同维数的掩码数组。每个维数应该包含奇数个元素。
  rank:一个非负整数，从排序列表中选择元素(0对应最小的元素，1是下一个最小的元素，等等)。
• 输出：
  与输入相同大小的数组。

import numpy as np
from scipy import signal

x = np.arange(25).reshape(5, 5)
domain = np.identity(3)
>>>x
array([[ 0,  1,  2,  3,  4],
       [ 5,  6,  7,  8,  9],
       [10, 11, 12, 13, 14],
       [15, 16, 17, 18, 19],
       [20, 21, 22, 23, 24]])
>>>signal.order_filter(x, domain, 0)
array([[  0.,   0.,   0.,   0.,   0.],
       [  0.,   0.,   1.,   2.,   0.],
       [  0.,   5.,   6.,   7.,   0.],
       [  0.,  10.,  11.,  12.,   0.],
       [  0.,   0.,   0.,   0.,   0.]])
>>>signal.order_filter(x, domain, 2)
array([[  6.,   7.,   8.,   9.,   4.],
       [ 11.,  12.,  13.,  14.,   9.],
       [ 16.,  17.,  18.,  19.,  14.],
       [ 21.,  22.,  23.,  24.,  19.],
       [ 20.,  21.,  22.,  23.,  24.]])