树的知识点与算法题
首先定义一个二叉树
#Definition for a binary tree node.
public class TreeNode{
int val;
TreeNode left;
TreeNode right;
TreeNode() {}
TreeNode(int val) {this.val = val}
TreeNode(int val, TreeNode left, TreeNode right){
this.val = val;
this.left = left;
this.right = right;
}
}
树的三种遍历方式
- 递归
- 前序遍历: 遍历树时先访问根结点,再依次访问左右结点。
class Solution {
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<Integer>();
preorder(root, res);
return res;
}
public void preorder(TreeNode root, List<Integer> res) {
if (root == null) {
return;
}
res.add(root.val);
preorder(root.left, res);
preorder(root.right, res);
}
}
- 中序遍历:遍历时先访问左结点,根结点在中间进行访问。因此只需要改变遍历访问顺序即可
public void inorder(TreeNode root, List<Integer> res) {
if (root == null) {
return;
}
inorder(root.left, res);
res.add(root.val);
inorder(root.right, res);
}
- 后序遍历:同理,将根结点的访问顺序放到最后即可
public void postorder(TreeNode root, List<Integer> res) {
if (root == null) {
return;
}
postorder(root.left, res);
postorder(root.right, res);
res.add(root.val);
}
- 迭代法
两种方式是等价的,区别在于递归的时候隐式地维护了一个栈,而我们在迭代的时候需要显式地将这个栈模拟出来,其余的实现与细节都相同。
对于后序遍历较为复杂,因为根结点在最后输出,因此需要两次入栈。
在后序遍历中,根结点是最后被访问的。因此,后序遍历过程中,当搜索指针指向某一根结点时,不能立即访问,而要先遍历其左子树,此时根结点进栈。当其左子树遍历完后再搜索到该根结点时,还是不能访问,还需遍历其右子树。所以,此根结点还需再次进栈,当其右子树遍历完后再退栈到到该根结点时,才能被访问。
在下列代码中,如果右子结点被遍历过且输出了,就会将其变为prev作为其根结点是否输出的条件
// 后序遍历!
class solution{
public List<Integer> postorderTraversal(TreeNode root){
List<Integer> res = new ArrayList<Integer>();
if(root == null){
return res;
}
Deque<TreeNode> stack = new LinkedLisk<TreeNode>();
TreeNode prev = null;
while( root != null || !stack.isEmpty()){
while(root != null){ //不断循环,先找到最左边的结点。
stack.push(root);
root = root.left;
}
root = stack.pop(); //使root结点等于左子结点
if( root.right == null || root.right == prev){
res.add(root.val);
prev = root;
root = nulll
}else{
stack.push(root);
root = root.right;
}
}
return res;
}
}
// 当左子结点弹出后,由于其右子结点为空,因此要向上弹出它的根结点,此时使得root结点为null,
// 但是stack不为空,因此会触发循环,使得根结点弹出,这时候会再进行判断该结点的右子结点,
// 不为空则将根结点先压进栈,再把右结点压入栈
对于中序遍历,可以一直向左遍历,并且在遍历途中先将根结点和压入栈中,然后弹出左叶子结点后先判断是否其存在右结点(左结点在循环中已经判断),如果不存在则将其根结点进行弹出并输出,再判断上一结点的右结点。
// 中序遍历!
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<Integer>();
if (root == null){
return res;
}
Deque<TreeNode> stack = new LinkedList<TreeNode>();
while(root != null || !stack.isEmpty() ){
while(root != null){
stack.push(root); // 遍历到最左边的结点
root=root.left;
}
root = stack.pop(); // 弹出左结点
res.add(root.val);
root = root.right; // 判断是否存在右子结点,如果存在则会重新遍历该右子结
//点的左子树,如果不存在则会弹出栈中的根结点。
}
return res;
}
}
对于先序遍历,遍历到根结点后,先判断右结点是否为空,不为空则压入栈中,然后判断左结点,由于右结点在左结点的下面,因此输出会按照根左右的顺序,符合先序遍历。
// 先序遍历!
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<Integer>();
if (root == null){
return res;
}
Deque<TreeNode> stack = new LinkedList<TreeNode>();
if(root != null){
stack.push(root);
}
while(root != null && !stack.isEmpty() ){
root = stack.pop(); //要注意弹出的不能为null,因此循环中需要判断stack不为空
res.add(root.val);
if(root.right != null){
stack.push(root.right);
}
if(root.left != null){
stack.push(root.left);
}
}
return res;
}
}
树的深度与高度
树的高度(深度):
有两种定义,一是根结点深度为从0开始,二是根结点深度从1开始
- 从根节点到最深节点的最长路径的节点数
- 从根到最深节点的最长路径的边数。
高度: 从下往上数,从该节点到叶子结点的最长简单路径边的条数。
深度: 从上往下数,从根节点到该结点的最长简单路径边的条数。
所以树的高度和深度是相等的,但是其他结点来说不一定相等。
树的高度定义函数:
h
e
i
g
h
t
(
r
o
o
t
)
=
{
0
r
o
o
t
=
n
u
l
l
max
{
h
e
i
g
h
t
(
r
o
o
t
.
l
e
f
t
)
,
h
e
i
g
h
t
(
r
o
o
t
.
r
i
g
h
t
)
}
+
1
r
o
o
t
!
=
n
u
l
l
height(root) = \begin{cases} 0 & root = null \\ \max\{height(root.left),height(root.right)\} +1 & root !=null \end{cases}
height(root)={0max{height(root.left),height(root.right)}+1root=nullroot!=null
-
算法思路
-
递归法
如果我们知道了左子树和右子树的最大深度 ll 和 rr,那么该二叉树的最大深度即为
max
(
l
e
f
t
,
r
i
g
h
t
)
+
1
\max(left,right) + 1
max(left,right)+1
而左子树和右子树的最大深度又可以以同样的方式进行计算。因此我们可以用「深度优先搜索」的方法来计算二叉树的最大深度。具体而言,在计算当前二叉树的最大深度时,可以先递归计算出其左子树和右子树的最大深度,然后在 O(1)时间内计算出当前二叉树的最大深度。递归在访问到空节点时退出。
class Solution {
public int maxDepth(TreeNode root) {
if (root == null) {
return 0;
} else {
int leftHeight = maxDepth(root.left);
int rightHeight = maxDepth(root.right);
return Math.max(leftHeight, rightHeight) + 1;
}
}
}
- 广度优先搜索
由于深度的另一个定义是该树的最大层数,因此可以用一个队列进行树的遍历,且每次循环时要保证队列中只存在某一层的全部结点,该层循环结束后,将深度递增。
class Solution {
public int maxDepth(TreeNode root) {
if(root == null){
return 0;
}
Queue<TreeNode> queue = new LinkedList<TreeNode>();
queue.offer(root);
int ans = 0;
while(!queue.isEmpty()){
int size = queue.size(); //每次循环重新定义size大小,保证在内循环中将队列中的元素旧元素全部出队列
while(size > 0){
TreeNode node = queue.poll(); //每次内循环得到队列中的结点,使得在接下来可以把该结点的子结点加入到队列中
if(node.left != null){
queue.offer(node.left);
}
if(node.right != null){
queue.offer(node.right);
}
size --;
}
ans ++;
}
return ans;
}
}
循环队列长度
leetcode相关题目
在努力学习数据结构与算法中,与树有意思的相关题目会持续更新,希望大家一起进步。
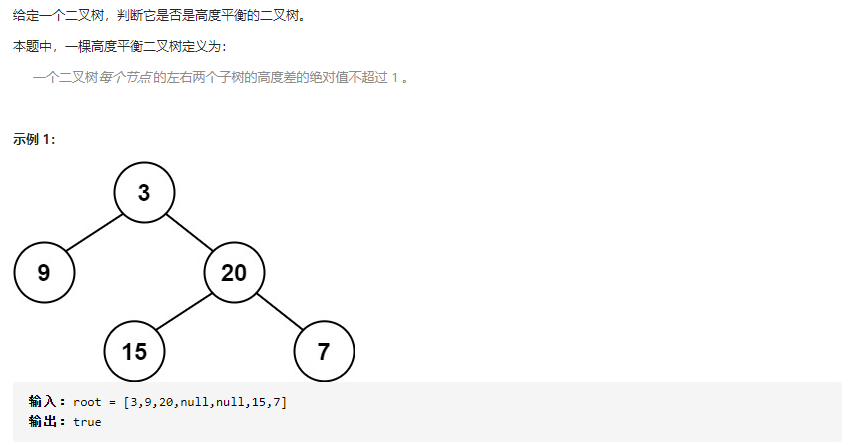
110.平衡二叉树
定义: 二叉树的每个节点的左右子树的高度差的绝对值不超过 1,则二叉树是平衡二叉树。
- 解题思路
1.自顶向下: 根据题意,最简单的思路是根结点的左子树-右子树的绝对值小于等于1,因此可以首先定义:
l
e
f
t
h
e
i
g
h
t
−
r
i
g
h
t
h
e
i
g
h
t
≤
1
leftheight-rightheight \leq1
leftheight−rightheight≤1
但是尽管根结点满足这个等式,其左右子树的子树不一定满足,因此下一个则需要求root.left,与root.right的高度,只有左右子树也都满足平衡二叉树的条件,该树才是平衡二叉树,因此这是个自顶向下的递归过程。
而在树的章节中提到,求树的深度(高度)可以定义函数:
h
e
i
g
h
t
(
r
o
o
t
)
=
{
0
r
o
o
t
=
n
u
l
l
max
{
h
e
i
g
h
t
(
r
o
o
t
.
l
e
f
t
)
,
h
e
i
g
h
t
(
r
o
o
t
.
r
i
g
h
t
)
}
+
1
r
o
o
t
!
=
n
u
l
l
height(root) = \begin{cases} 0 & root = null \\ \max\{height(root.left),height(root.right)\} +1 & root !=null \end{cases}
height(root)={0max{height(root.left),height(root.right)}+1root=nullroot!=null
class Solution {
public boolean isBalanced(TreeNode root) {
if(root == null){
return true;
}else{
return (Math.abs(height(root.left)-height(root.right)) <= 1 && isBalanced(root.left) && isBalanced(root.right));
}
}
public int height(TreeNode root){
if(root == null){
return 0;
}else{
return Math.max(height(root.left),height(root.right)) + 1;
}
}
}
2.自底向上: 对于第一种方法,如果采用自顶向下,那么balanced函数就会反复被调用,导致时间复杂度过高,因此可以相当于对树进行后序遍历,然后将每层的左子树高度与右子树高度相减进行判断,如果左右子树高度相差≥2,则不平衡,否则平衡并且返回该节点的高度。
class Solution {
public boolean isBalanced(TreeNode root) {
return height(root) >= 0;
}
public int height(TreeNode root) {
if (root == null) {
return 0;
}
int leftHeight = height(root.left);
int rightHeight = height(root.right);
if (leftHeight == -1 || rightHeight == -1 || Math.abs(leftHeight - rightHeight) > 1) {
return -1;
} else {
return Math.max(leftHeight, rightHeight) + 1;
}
}
}
实际上,对于上述代码由于平衡树的要求是各个节点的左右子树都需要平衡,因此如果左/右子树不平衡,则该树则不是平衡树,因此在判断右子树是否平衡时,可以首先判断左子树是否为平衡树,如果不是则停止递归,直接返回-1值,具体代码如下:
class Solution {
public boolean isBalanced(TreeNode root) {
return balanced(root) != -1;
}
private int balanced(TreeNode node) {
if (node == null) return 0;
int leftHeight, rightHeight;
//将计算和判断放在一起
if ((leftHeight = balanced(node.left)) == -1
|| (rightHeight = balanced(node.right)) == -1
|| Math.abs(leftHeight - rightHeight) > 1)
return -1;
return Math.max(leftHeight, rightHeight) + 1;
}
}
206.反转链表

对于链表与树的相关问题,主要方法是迭代遍历亦或者是递归的方法,这一题比较容易想到的是迭代法
1.迭代法
首先从头开始,对于head以及head.next的元素,我们希望head与head.next的元素的箭头相反,但是由于这是单向链表,因此需要定义两个变量用来保存这两个结点的值。
1
→
2
→
3
→
4
→
5
→
n
u
l
l
1\rightarrow2\rightarrow3\rightarrow4\rightarrow5\rightarrow null
1→2→3→4→5→null
第一次经过变化应变成
1
2
→
3
→
4
→
5
→
n
u
l
l
1 2\rightarrow3\rightarrow4\rightarrow5\rightarrow null
1 2→3→4→5→null
由此可见,2应变为head结点,而第三次变化如下
1
←
2
3
→
4
→
5
→
n
u
l
l
1\leftarrow2 3\rightarrow4\rightarrow5\rightarrow null
1←2 3→4→5→null
依次迭代,直至最后的head结点为null则停止迭代。而为了实现新的head指向旧的结点,应该设置两个变量,prev和cur,prev用来保存新的链的头节点,也就是上面的1或2,而cur则是在重新设置head结点时用来保存新结点的临时变量(cur = head.next),避免断开指针时无法找到下一结点的值。具体代码如下:
class Solution {
public ListNode reverseList(ListNode head) {
ListNode prev = null;
ListNode cur = null;
while(head != null){
cur = head.next;
head.next = prev;
prev = head;
head = cur;
}
return prev;
}
}
// 定义prev和cur是为了保证两个结点的数据不丢失,并且可以通过指向这个临时变量来保证箭头方向的准确。
2.递归法
本题的递归法很难想到,因为很多时候都会想着把最后一个结点移到指向第一个结点,这样就会很难进行操作,但是其实可以换一种思路,对于一个结点,我们可以把它的下一个结点箭头反转,也就是next.next结点指向它自己,而它的next结点则指向空,这样就可以保证对于该结点来说,他的下一个结点是反转的,这也是已处理的结果
n
1
→
.
.
.
→
n
k
−
1
→
n
k
→
n
k
+
1
→
.
.
.
→
m
→
n
u
l
l
n1\rightarrow ...\rightarrow nk-1\rightarrow nk\rightarrow nk+1 \rightarrow ... \rightarrow m \rightarrow null
n1→...→nk−1→nk→nk+1→...→m→null
当进行多次处理后,该链表应变为:
n
1
→
.
.
.
→
n
k
−
1
→
n
k
←
n
k
+
1
←
.
.
.
←
m
n1\rightarrow ...\rightarrow nk-1\rightarrow nk\leftarrow nk+1 \leftarrow ... \leftarrow m
n1→...→nk−1→nk←nk+1←...←m
根据链表中递归算法的表示,可以表示为
上
一
级
→
h
e
a
d
→
已
处
理
的
结
果
上一级 \rightarrow head \rightarrow 已处理的结果
上一级→head→已处理的结果
而我们在这一级中,我们希望把从head开始,右边的全变为已处理结果, 因此我们需要将指针反转,也就是head.next.next=head,而已处理结果则是运用递归时的返回值,也就是新的链表。
class Solution {
public ListNode reverseList(ListNode head) {
if (head == null || head.next == null){
return head;
}
ListNode newHead = reverseList(head.next);
head.next.next = head;
head.next = null;
return newHead;
}
}
222.完全二叉树的节点个数
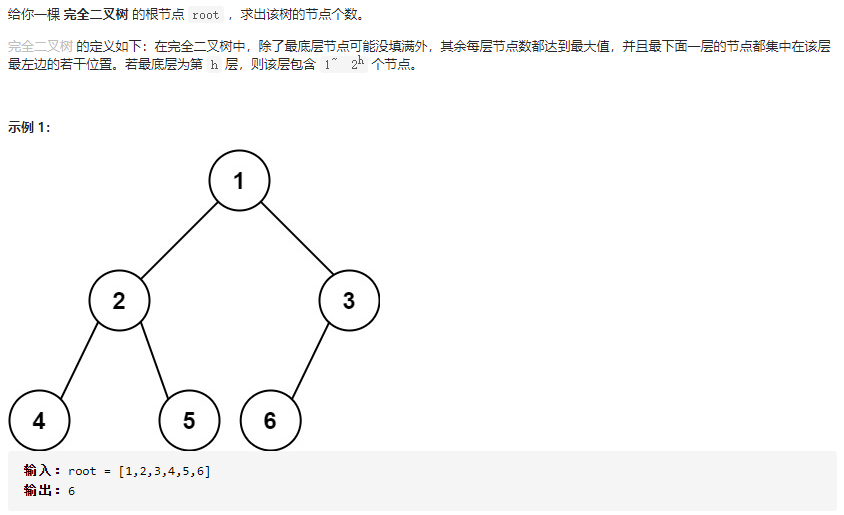
对于计算树的结点,我们一般可以想到使用递归的方法,这也回到了递归的三部曲,易想到应该返回该子树的结点数。
N
o
d
e
s
=
l
e
f
t
N
u
m
b
e
r
+
r
i
g
h
t
N
u
m
b
e
r
+
1
(
1
为
根
结
点
)
Nodes = leftNumber + rightNumber + 1(1为根结点)
Nodes=leftNumber+rightNumber+1(1为根结点)
作为递归的返回值。
1.暴力法
public int countNodes(TreeNode root) {
if (root == null){
return 0;
}
return countNodes(root.left) + countNodes(root.right) + 1;
}
但是该方法并没有很好的利用题目提供的条件,该树为完全二叉树,完全二叉树的定义是:倒数第二层的结点为满结点,而最后一层的结点为左连续结点,因此右子树最后一个结点能有两种情况,一是跟左子树的最后一个结点在同一层,二是在左子树结点的上一层,我们知道,对于满二叉树,它的结点总数为
2
h
−
1
(
h
为
树
的
高
度
)
\pmb{2^h-1(h为树的高度)}
2h−1(h为树的高度)2h−1(h为树的高度)2h−1(h为树的高度)
因此,对于第一种情况,当左子树和右子树的最后一个结点在最后一层时,那么左子树一定时满二叉树,这时左子树结点加上根结点的计算公式为
2
h
−
1
+
1
2
=
2
h
−
1
=
2
l
{\frac{2^h-1+1}{2}=2^{h-1}=2^l }
22h−1+1=2h−1=2l
此时l为左子树的高度
而对于第二种情况,右子树为满二叉树,同时加上根节点,总结点数为
2
r
−
1
+
1
=
2
r
{2^r-1+1=2^r}
2r−1+1=2r
而由于完全二叉树的每颗子树也是完全二叉树,因此可以计算一部分,剩余部分仍然可以按照上面两种情况进行结点计算,即递归
class Solution {
public int countNodes(TreeNode root) {
if (root = null){
return 0;
}
int leftHeight = countLevel(root.left);
int rightHeight = countLevel(root.right);
if(left == right){
return countNodes(root.right) + (1<<left);
}else{
return countNodes(root.left) + (1<<right);
}
}
private int countLevel(TreeNode root){
int level = 0; //从0开始,保证子树的高度计算正确。
while(root != null){
level ++;
root = root.left
}
return level;
}
}
小tips:
<<左移: 右边空出的位置补0,其值相当于乘以2。
2的次方运算可以通过将1移位来计算,1<<1,表示将1向左移1位,这时候1变为10,此时在二进制中10表示为十进制的2,也就是
2
1
2^1
21,因此
2
n
=
1
<
<
n
2^n = 1<<n
2n=1<<n。
>>右移: 左边空出的位,如果是正数则补0,相当于除以2 若为负数则补0或1,取决于所用的计算机系统OS X中补1
同上述例子,右移则会将10变为1,也就是将十进制中的2变为1,相当于除以2。
x
2
n
=
x
>
>
n
\frac{x}{2^n}=x>>n
2nx=x>>n
证明:完全二叉树的子树也为完全二叉树
证明:让T是一棵完全二叉树, S是它的一棵子树。由子树定义可知,s是由T中某个结点及其所有子孙构成的。由于T是完全二叉树,T的所有叶子结点都在两个相邻的层次上。因此,S的所有叶子结点都在两个相邻的层次上。类似的,如果在S中存在不位于底层上结点层,那么,该层也不位于T的底层上,它必须在T中所有底层叶子结点的右边,因此它也必须在S中所有底层叶子结点的右边。从而得到S是完全二叉树。
814.二叉树剪枝
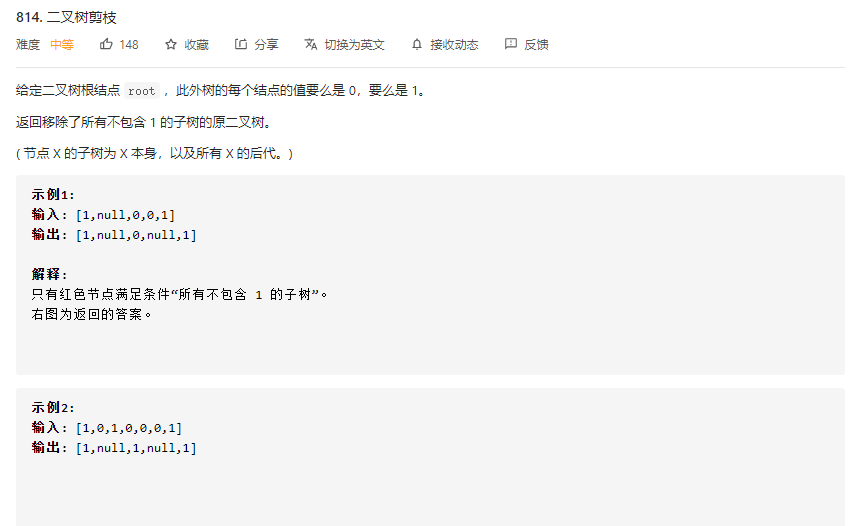
本题主要意思是指将全为0的二叉树删去,即将该子树的根结点设为null。具体例子如图所示
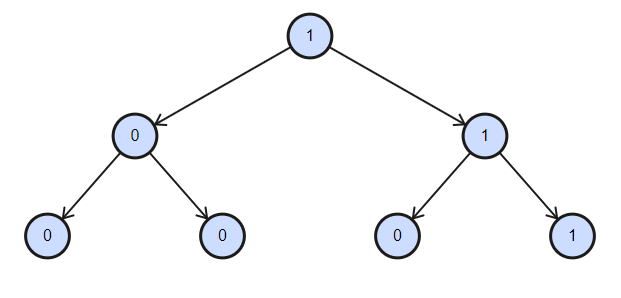
开始判断,应该想到从底层开始往上遍历,因为首先要判断叶子结点是否为1,如果不为1,即为0,这时候就要将该叶子结点设为null,因为该结点的左右子结点都为null,不符合题目要求包含1的子树的条件。对于左叶子结点,判断一次,此时再判断右叶子结点,进行相应的操作。由此可知剪枝是个递归的过程。
对于一个结点,该结点是否为1,如果为1那么左右子结点不论是什么,都可以保留。而如果该结点为0,那么就要判断左右结点是否为0或者null,而左右结点是否为null又是由它的左右子结点决定的,因此要进行后序遍历。
//单看一个结点及其左右子结点,判断条件为:
if(root.val == 0 && root.left == null && root.right == null){
root = null;
}
// 而root.left 和root.right 应该继续递归,且在这个判断之前,即为后序遍历。
class Solution {
public TreeNode pruneTree(TreeNode root) {
if(root == null){
return null; //递归结束条件
}
root.left = pruneTree(root.left);
root.right = pruneTree(root.right);
if(root.left == null && root.right == null && root.val == 0){
root = null;
}
return root;
}
}
小结:
对递归的理解不够深刻,尽管对于什么时候停止递归有了思路,但是结合题目要求的判断条件的想法不够清晰,而递归时,应该就考虑当前结点和其子结点,考虑过多的结点会造成思路的混淆。
257.二叉树的所有路径

这一题,其实跟前序遍历二叉树的想法类似,都是先对树的根结点先进行处理,然后将其存入一个列表,如果他不是叶子结点,那么就要对其左结点和右结点进行相同的操作,同样是先对左结点或右结点进行处理存储,再继续判断往下递归。如果递归到是叶子结点,那么这时候就应该返回存储的路径。
难点: 对字符串的处理,List的使用以及对树的前序遍历。
class Solution {
public List<String> binaryTreePaths(TreeNode root) {
List<String> paths = new ArrayList<String>();
construcPaths(root, "", paths);
return paths;
}
private void construcPaths(TreeNode root, String path, List<String> paths){
if(root != null){
StringBuffer sb = new StringBuffer(path);
sb.append(Integer.toString(root.val));
if(root.left == null && root.right == null){
paths.add(sb.toString());
}else{
sb.append("->");
construcPaths(root.left, sb.toString(), paths);
construcPaths(root.right, sb.toString(), paths);
}
}
}
}
111.二叉树的最小深度
问题: 给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
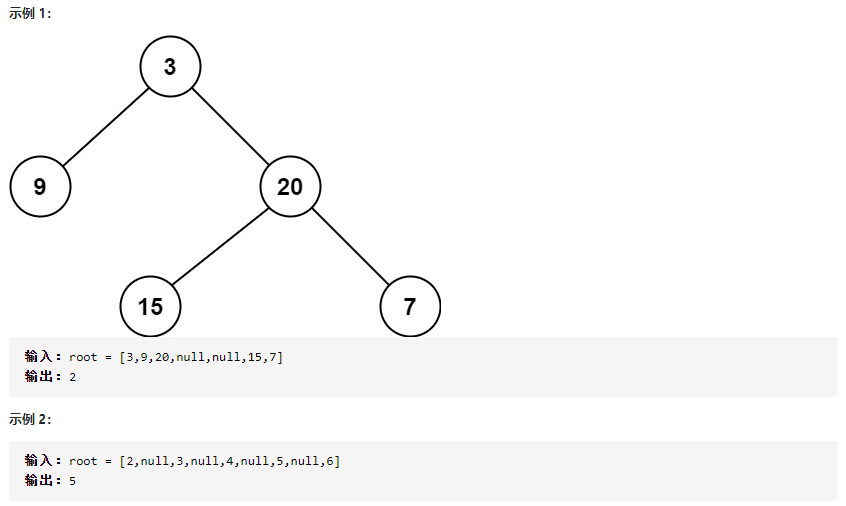
思路:
递归法:(深度优先搜索)
由于这道题的题目是二叉树的最小深度,因此很容易联想到之前做过的求二叉树的深度的题目,那题是利用递归的做法,求出每个节点的高度并返回,最后求出整个树的深度。因此很容易得到下列代码
class Solution {
public int minDepth(TreeNode root) {
if (root == null) {
return 0;
} else {
int leftHeight = maxDepth(root.left);
int rightHeight = maxDepth(root.right);
return Math.min(leftHeight, rightHeight) + 1;
}
}
}
但是这题的条件有所不同,如果是求每个结点的最小深度,那么题目中示例2是不满足的,因为没有判断根结点会不会是叶子结点的情况,如果根结点的左右结点有一个不为空,那么就不能直接计算该结点的深度,应该继续向左右结点进行递归,直到找到叶子结点,从而返回深度。
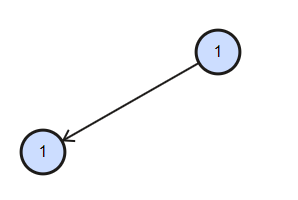
由于递归只需要考虑当前结构的情况,因此对于上图,右结点为空的情况下,这时候我们需要返回的是左右结点深度的最大值,左结点为空的情况则同理。
class Solution {
public int minDepth(TreeNode root) {
if (root == null) {
return 0;
}
int leftHeight = maxDepth(root.left);
int rightHeight = maxDepth(root.right);
if(root.left == null || root.right == null){
return Math.max(leftHeight, rightHeight) + 1;
}
else {
return Math.min(leftHeight, rightHeight) + 1;
}
}
}
广度优先搜索:
对于递归法,由于需要对每个结点都进行判断,因此时间复杂度为O(n),而空间复杂度最坏情况则为O(n),就如同示例2,树为链表形状。而如果使用BFS,在第一次找到叶子结点时,就可以直接返回深度,不需要继续往下找到最后的叶子结点。
class Solution {
public int minDepth(TreeNode root) {
if(root == null){
return 0;
}
Queue<TreeNode> queue = new LinkedList<TreeNode>();
queue.offer(root);
int ans = 1;
while(!queue.isEmpty()){
int size = queue.size(); //每次循环重新定义size大小,保证在内循环中将队列中的元素旧元素全部出队列
while(size > 0){
TreeNode node = queue.poll(); //每次内循环得到队列中的结点,使得在接下来可以把该结点的子结点加入到队列中
if(node.left == null && node.right ==null){
return ans;
}
if(node.left != null){
queue.offer(node.left);
}
if(node.right != null){
queue.offer(node.right);
}
size --;
}
ans ++;
}
return 0;
}
}
100.相同的树,101.对称二叉树
这两天做了两道二叉树的题目,发现做下来后两者的代码思路比较类似,于是将它们一起记录下来。
100.相同的树,题目描述:
给你两棵二叉树的根节点 p 和 q ,编写一个函数来检验这两棵树是否相同。如果两个树在结构上相同,并且节点具有相同的值,则认为它们是相同的。
示例:
输入: p = [1,2,3], q = [1,2,3]
输出: true
输入: p = [1,2], q = [1,null,2]
输出: false
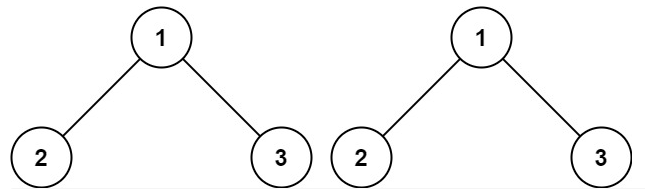
101.对称二叉树,题目描述:
给定一个二叉树,检查它是否是镜像对称的。
示例:
input: root= [1,2,2,3,4,4,3]
Output: true
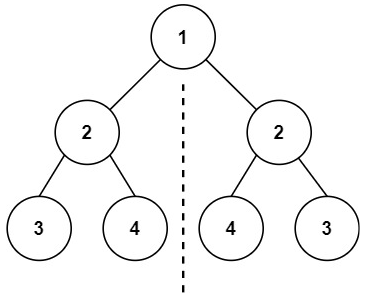
这两题,我们很容易想到使用递归的方法,因为我们还是可以将一个树,抽象看成根结点以及左右结点,对于相同二叉树,我们首先就应该判断两个树根结点是否存在,如果存在就要判断根结点的值是否相等,不相等就直接返回false,相等则开始比较左结点与右结点。这里我们要注意的是,当p树的左结点存在而q树的左结点不存在,这时候应该直接返回false。当由于我们把左右子树看成一个结点,调用递归函数时,上一次函数的左结点,将会是下一个递归函数的根结点,因此我们只需要在函数中加入判断,p的根结点或q的根结点只有一个存在时,也返回false。
同理,对称二叉树也是同样的代码思想,只是我们首先需要根结点是否存在,其次将左右树变成两个单独的树进行比较,比较思想同上。
// 相同的树递归做法
class Solution {
public boolean isSameTree(TreeNode p, TreeNode q) {
if(p == null && q == null){
return true;
}
if(p != null && q != null){
if(p.val != q.val){
return false;
}
return isSameTree(p.left, q.left) && isSameTree(p.right, q.right);
}
return false;
}
}
// 对称二叉树递归做法
class Solution {
public boolean isSymmetric(TreeNode root) {
return check(root, root);
}
public boolean check(TreeNode p, TreeNode q) {
if (p == null && q == null) {
return true;
}
if (p == null || q == null) {
return false;
}
return p.val == q.val && check(p.left, q.right) && check(p.right, q.left);
}
}
// 做法原理基本一样,只是下面的函数代码层次比较清晰,更加便于阅读。
// 对称二叉树的迭代做法
class Solution {
public boolean isSymmetric(TreeNode root) {
return check(root, root);
}
public boolean check(TreeNode u, TreeNode v) {
Queue<TreeNode> q = new LinkedList<TreeNode>();
q.offer(u);
q.offer(v);
while (!q.isEmpty()) {
u = q.poll();
v = q.poll();
if (u == null && v == null) {
continue;
}
if ((u == null || v == null) || (u.val != v.val)) {
return false;
}
q.offer(u.left);
q.offer(v.right);
q.offer(u.right);
q.offer(v.left);
}
return true;
}
}
小tips:
&&符号在第一次判断时如果为false则直接返回,不会再进行判断后面的语句。






















 623
623











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








