白话解析B+树并附Java完整实现

B+树是一种树数据结构，通常用于数据库和操作系统的文件系统中。B+树的特点是能够保持数据稳定有序，其插入与修改拥有较稳定的对数时间复杂度。B+树被用于MySQL数据库的索引结构。这里为了便于大家理解，我基于内存（因为数据量的原因，实际上的B+树应该基于磁盘等外存，基于内存的比较适合作为Demo，同时还可以作为一种多路搜索树）实现了B+树的增删查改操作（包括节点分裂和节点合并），并开源在了：GitHub - Morgan279/MemoryBasedBPlusTree: An implementation of B+Tree (a multiway search tree based on the memory, i.e., all data records are stored in the memory instead of the disk).。

B+树的重要前置概念

B+ 树是一种树数据结构(一个n叉树)，这里我们首先介绍B+树最重要的概念：B+树节点。一棵B+树的节点包含非叶节点和叶子节点两类：

非叶节点

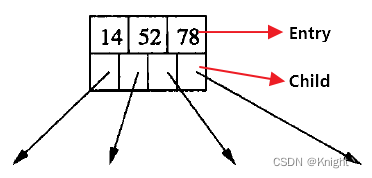
如上图所示，非叶节点包含两部分信息：

• Entry: 索引键，用于索引数据，它必须是可比较的，在查找时其实也是根据Entry的有序性来加快查找速度（原理和二分查找类似，通过有序性来剪枝搜索空间，所以是对数级的实际复杂度）
• Child: 指向其孩子节点的指针，可以通过它访问到该非叶节点的子节点

对于非叶节点来说，Child孩子指针的数量总是等于Entry的数量加1，也就是说一个非叶节点如果有3个Entry的话，那么就可以得到它有 3+1=4 个孩子（子节点）。

叶节点

如上图所示，叶节点包含三部分信息：

• Entry: 与非叶节点中的Entry一致，用于索引数据
• Data指针: 用于指向具体数据的指针（从这里可以发现，非叶节点的指针只能找到它的孩子的地址，而真正的数据的地址只能通过叶节点找到，即可以理解为所有数据都存储在叶节点上）
• Next指针: 用于指向该叶节点的后面一个叶子节点，最后一个叶子节点的Next指针为空（Next指针存在的意义是加快范围查询）。

 对于叶节点来说，Data数据指针的数量总是等于Entry的数量，也就是说一个叶节点如果有3个Entry的话，那么就可以得到它索引了3个数据项，这里与非叶节点不同的原因是叶节点分出了一个指针去指向了下一个叶节点，所以其实无论是非叶节点还是叶节点，他们Entry数量和指针数量的关系都是：指针数量等于Entry数量加1。

为了使逻辑更加清晰，后面我在介绍”B+树的操作“时将会按非叶节点和叶节点分别进行讨论。

阶数

一棵B+树通常用 m 来描述它的阶数，它的作用是描述一个B+树节点中Entry数量的上限和下限。在大多数对于B+树的介绍了，一般描述一个m阶的B树具有如下几个特征:

1.根结点至少有两个子女。

2.每个中间节点都至少包含ceil(m / 2)个孩子，最多有m个孩子。

3.每一个叶子节点都包含k-1个元素，其中 m/2 <= k <= m。

4.所有的叶子结点都位于同一层。

5.每个节点中的元素从小到大排列，节点当中k-1个元素正好是k个孩子包含的元素的值域分划

上面的特征可能看起来会比较复杂，所以这里用我自己的一个更简单的理解来解释一下。我们设一个B+树节点的Entry数量上限为Key_Bound，简写为K,

则 K = m - 1。得到K之后，获取Entry数量的下限也变得很简单，就是 K / 2 （整型除法，下取整）

根据我们上面对B+树节点的介绍，我们可以根据K得到很轻松地得到节点中对应指针的数量: K + 1。

用代码表示如下：

public BPlusTree(int order) {
   this.KEY_UPPER_BOUND = order - 1; //Entry 上限
   this.UNDERFLOW_BOUND = KEY_UPPER_BOUND / 2; //Entry 下限
}

这样我们拿到了B+树中Entry的上限、下限及对应的指针数量之后，后面我们就可以不必再理会那个计算更复杂的m了。

在实际的应用中，B+树的阶数其实越大越好，因为当B+树的阶数越大，B+树一个节点所能容纳的Entry就会越多，B+树就会变得更”矮“，而更”矮“意味着更少的磁盘I/O，所以一般情况下B+树的阶数跟磁盘块的大小有关。

B+树的操作

等值查询(query)

B+树的等值查询指：找到B+树叶节点Entry与查询Entry完全相等所对应的数据，等值查询的过程主要是依赖于Entry的有序性：设B+树某个节点的Entry e 是第index个Entry，则该节点的第index个孩子中的所有Entry都是小于e的，该节点的第index+1个孩子中的所有Entry都是大于等于e的。所以我们可以根据这个有序性，自顶向下逐层查找，最终找到匹配的叶子节点然后获取到数据。

对于非叶节点，只需要找到第一个大于查询Entry的子节点，即 upper bound（如果所有子节点都小于等于查询Entry，则 uppber bound 为子节点的数量），然后如此递归地让这个子节点进行查找即可。其中最关键的就是找到第一个大于查询Entry的子节点 upper bound，因为查询Entry只可能出现在upper bound 的前一个位置。由于B+树Entry的有序性，在这里我们可以使用二分搜索实现这一点，因为二分搜索的效率非常高（O(logN)级别），代码实现如下：

        protected int entryIndexUpperBound(K entry) {
            int l = 0;
            int r = entries.size();
            while (l < r) {
                int mid = l + ((r - l) >> 1);
                if (entries.get(mid).compareTo(entry) <= 0) {
                    l = mid + 1;
                } else {
                    r = mid;
                }
            }