【JZOJ5698】【GDOI2018 day1】密码锁（lock）（差分）

Problem

　　给出一个长度为n序列a，其中的每个数在0到m-1之间。每次操作可以选取一个区间，使区间内的数区间+1或-1（在模m的意义下）。求最少需要多少次操作才能将序列变成n个0。

Hint

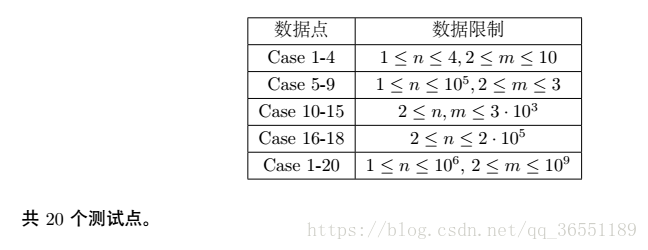
Solution

　　比赛时，我感觉这道题比较诡谲，胡思乱想了一会，发现切不了，于是将重心放在骗分上。

20points：bfs

　　我一眼发现前4个点的n极小无比，可以手玩。
　　具体分析一下，这种题很适合bfs。由于n只有4，m只有10，不妨直接将序列a设为状态。bfs的起点即为它给出的a，终点即为{0,0,0,0}。这样的话，状态数总共有$O(m^n)$；而对于每一个状态，转移数为$O(\frac{n(n+1)}2（区间数目）*2（加操作或减操作）)$。所以：
　　时间复杂度：$O(m^nn^2)$。

Code

　　表示我并没有拿到我比赛时打的代码╮(╯▽╰)╭，我也懒得再打一遍，毕竟这也很水。

30points：贪心

　　第5-9个点的限制是2≤m≤3。
　　我先想m=2的情况。此时，a中只有0/1，所以加减操作都是一样的，都是将区间中的数取反。那么可以举个栗子分析一下。
　　设a为{00011001001110011010}，则如果我们要对区间[4,19]进行操作，那么里面的5块连续的1会变成0，而里面还有4块连续的0会变成1。所以说，如果我们某次操作的边界都是1（这样显然是最优的），并且我们使[l,r]中的x块连续的1变成了0，那么我们肯定会使其中的x-1块连续的0变成1。于是每次操作只会减少x-(x-1)=1块连续的1。所以Ans=连续的1的块数。
　　时间复杂度：$O(n)$。
　　然后我接着想m=3的情况，没想出个所以然来，还白白浪费了10minutes左右的时间。。。
　　不过，我在比赛时并未打m=2的特判，而只打了20points的bfs：一是因为时间关系；二是在比赛时我并没有这么严谨的证明（其实是不够自信）。
　　听过讲的都知道了，m=2的有2个点，所以这种方法是30points的；至于m=3的情况，出题人都不知道。。。

Code

　　首先，我没有打；其次，我纵然打了也拿不到代码╮(╯▽╰)╭。

100points：差分

　　（我发现这似乎是我做过的第一道差分题）
　　首先，我们可以对a求个差分表dif。如果你弱得和几天前的我一样不知道什么叫差分表，我就友情提醒一下：求法即$\forall_{0≤i≤n}dif[i]=a[i+1]-a[i]$。由于本题是在模m的意义下的，所以不妨给dif[i]模个m。
　　本题的操作是区间+1或-1。如果是使区间[l,r]+1，那就相当于使dif[l]+1,dif[r+1]-1；如果是区间-1，则相当于使dif[l]-1,dif[r+1]+1。以区间+1为例，使区间[l,r]+1会使a[l]与a[l-1]的差+1，所以dif[l]+1；而对于l~r中的数，相邻的两数的差并不会改变；但又会使a[r+1]与a[r]的差-1，所以dif[r+1]-1。
　　它要求你将a清零，其实就相当于将dif清零。因为当dif={0,0,…,0}时，a[0]=0，a[1]=a[0]+dif[0]=0，以此类推，a={0,0,…,0}。
　　于是，原问题就被转化成每次操作使dif中的某个数+1，某个数-1（+1和-1均为模m意义下），并让你求将dif清零最少需要多少次操作。
　　这个有解吗？肯定是有的，因为当你不模m的时候，可知下式：

$$\sum_{i=0}^n dif[i]=a[1]-a[0]+a[2]-a[1]+a[3]-a[2]+...+a[n+1]-a[n]=a[n+1]-a[0]=0$$

　　而dif[i]中可能含有负数，模m相当于+m，所以最终$\sum_{i=0}^n dif[i]$绝对是m的倍数。当你只是进行普通的操作时（即不会使某个dif[i]+1到m，卒致将它模成0），$\sum_{i=0}^n dif[i]$的值是不会变的；如果将某个dif[i]+1变成了m，又把它模成0，则相当于使$\sum_{i=0}^n dif[i]$的值减少了一个m。所以最终肯定会将$\sum_{i=0}^n dif[i]$减成0。
　　那么我们可以考虑给dif[i]从大到小排个序，尽量先减dif[i]小的，加dif[i]大的。
　　当然，我们不能一次一次地加减，毕竟m还是很大的，我们这么磨蹭肯定要操作很多次；所以可以正着求一波dif[i]的前缀和，倒着求一波m-dif[i]的后缀和，枚举加减操作的交点，直接判断前后缀和是否相等即可。
　　时间复杂度：$O(nlog_2n)$（快排）。

槽点

　　据zjq的提醒，51nod上题号为1357的题是一道原题，题目名字都一样（虽然说这题数据更大）。不过我还是相信出题人和组题人在知乎上的回答，他们应该是不知道有这么一道题（只有像我这样的蒟蒻才屑于去刷51nod上的6级算法题吧，dalao肯定都不屑一顾），故才撞题的。
　　不过，这也使我的51nod账号又多了160points嘛(^▽^)。

Code

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
#define ll long long
#define fo(i,a,b) for(i=a;i<=b;i++)
#define fd(i,a,b) for(i=a;i>=b;i--)
const int N=1e6+2;
int i,n,m,a[N],now,next,dif[N];
ll sum1[N],sum2[N];

void scan()
{
    scanf("%d%d",&n,&m);
    fo(i,1,n)scanf("%d",&a[i]);
}

void differ()
{
    now=0;
    fo(i,0,n)
    {
        next=(a[i+1]+m)%m;
        dif[i]=(next-now+m)%m;
        now=next;
    }   
}

void work()
{
    sort(dif,dif+n+1);

    sum1[0]=dif[0];
    fo(i,1,n)sum1[i]=sum1[i-1]+(ll)dif[i];

    sum2[n+1]=0;
    fd(i,n,1)
        if((sum2[i]=sum2[i+1]+(ll)(m-dif[i])%m)==sum1[i-1])
        {
            printf("%lld\n",sum2[i]);
            break;
        }
}

int main()
{
    freopen("lock.in","r",stdin);
    freopen("lock.out","w",stdout);
    scan();
    differ();
    work();
}