扩展欧几里得
当 a 与 b 互素时有 gcd ( a , b ) = 1 ;
即得: a * x + b * y = 1;
a * x ≡ 1 ( mod b );
由于 a 与 b 互素,同余式两边可以同除 a ,得:
1 * x ≡ 1 / a (mod b);
x就是a%b的逆元
费马小定理(Fermat's little theorem)是数论中的一个重要定理,在1636年提出,其内容为: 假如p是质数,且gcd(a,p)=1,那么 a^(p-1)≡1(mod p),即:假如a是整数,p是质数,且a,p互质(即两者只有一个公约数1),那么a的(p-1)次方除以p的余数恒等于1。
欧拉定理
a^(φ(m))≡1(mod m) (a与m互质)
φ(n)=n * (1-1/p1) * (1-1/p2) ********(1-1/pn) p[1~n]为小于n的素数
//求单个数的欧拉函数:
int euler_phi(int n)
{
int res = n;
int m = (int)sqrt(n);
for(int i = 2; i <= m; i++)
if(n % i == 0)
{
res = res / i * (i-1);
while(n % i == 0) n /= i;
}
if(n > 1) res = res / n * (n-1);
return res;
}
//筛选法求欧拉函数
void euler_phi()
{
for(int i = 1; i < N; i++) phi[i] = i;
for(int i = 2; i < N; i++)
if(phi[i] == i) //成立说明i是素数
for(int j = i; j < N; j += i) //j要从i开始,这样可以处理素数的情况
phi[j] = phi[j] / i * (i-1);
}
void Get_phi()///筛法求欧拉函数
{
cnt = 0;
memset(flag, true, sizeof(flag));
phi[1] = 1;
for(int i=2; i<MAXN; i++)///线性筛法
{
if(flag[i])///素数
{
p[cnt++] = i;
phi[i] = i-1;///素数的欧拉函数值是素数 - 1
}
for(int j=0; j<cnt; j++)
{
if(i*p[j] > MAXN)
break;
flag[i*p[j]] = false;///素数的倍数,所以i*p[j]不是素数
if(i%p[j] == 0)///性质:i mod p == 0, 那么 phi(i * p) == p * phi(i)
{
phi[i*p[j]] = p[j] * phi[i];
break;
}
else
phi[i*p[j]] = (p[j]-1) * phi[i];///i mod p != 0, 那么 phi(i * p) == phi(i) * (p-1)
}
}
}
求幂大法 gcd(a,m)>1&&b>φ(m) a^b≡a^(b%φ(m)+φ(m))(mod m)
一种通用的求逆元方法,适合(b|a)。公式如下
现在我们来证明它,已知
逆元打表
有时会遇到这样一种问题,在模质数p下,求1~n逆元 n< p(这里为奇质数)。可以O(n)求出所有逆元,有一个递推式如下
inv[i]=(M-M/i)*inv[M%i]%M
它的推导过程如下,设t=M/i,k=M%i,那么
==>t*i+k≡0( mod M)
==>-t*i≡k( mod M)
对上式两边同时除i*k,进一步得到
==> -t/k≡1/i(mod M)//逆元
==> -t*inv[k]≡inv[i](mod M)
再把t和k替换掉,最终得到
inv[i]=(M+M/i)*inv[M%i]%M
初始化inv[1]=1,这样就可以通过递推法求出1->n模奇素数p的所有逆元了。
另外有个结论模1->p的所有逆元值对应1->中所有的数,比如p=7,那么1->6对应的逆元是1 4 5 2 3 6。
typedef long long ll;
const int N = 1e5 + 5;
int inv[N];
void inverse(int n, int p) {
inv[1] = 1;
for (int i=2; i<=n; ++i) {
inv[i] = (ll) (p - p / i) * inv[p%i] % p;
}
}







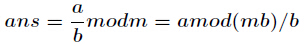
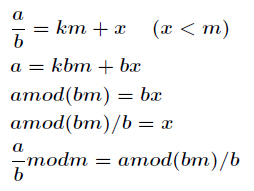














 1868
1868

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








