二叉树-前序、中序、后序（含python实现）

二叉树

二叉树属于树的一种，其每个节点最多有两个子节点。二叉树在数据结构中应用十分广泛。
常见的二叉树有：

1. 平衡二叉搜索树：又被称为AVL树，有以下性质：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。
   
   
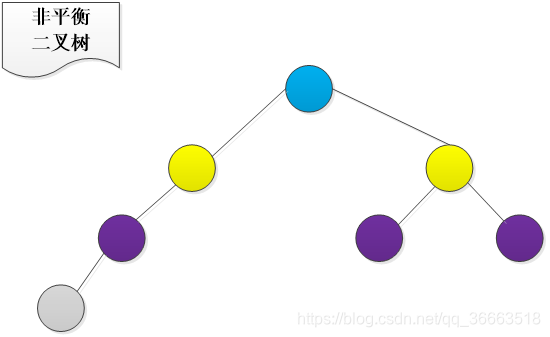
2. 满二叉树：高度为n的满二叉树有$2^n-1$个节点。
   
3. 完全二叉树：上层全满，最下层从左到右顺序排列。
   
   
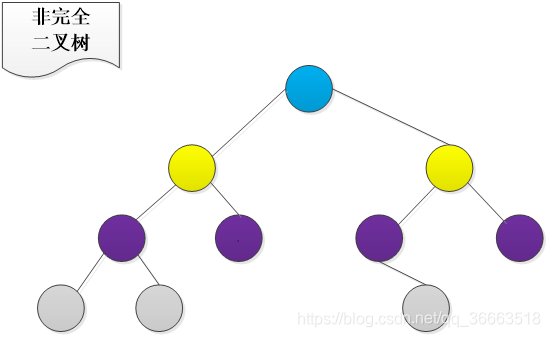
   为了方便下文对二叉树的实例讲解，这里初始化一个二叉树类：

class BinaryTree:
    def __init__(self, data):
        self.data = data
        self.left = None
        self.right = None

    def get(self):
        return self.data

    def getLeft(self):
        return self.left

    def getRight(self):
        return self.right

    def setLeft(self, node):
        self.left = node

    def setRight(self, node):
        self.right = node

构造一个二叉树实例：

binaryTree = BinaryTree('A')    
binaryTree.setLeft(BinaryTree('B'))    
binaryTree.setRight(BinaryTree('C'))    
binaryTree.getLeft().setLeft(BinaryTree('D'))    
binaryTree.getLeft().setRight(BinaryTree('E'))    
binaryTree.getRight().setLeft(BinaryTree('F'))    
binaryTree.getRight().setRight(BinaryTree('G'))

其结构如下：

前序遍历

前序、中序、后序都是对树的一种遍历操作，按照一定规则访问树中的每一个节点。
前序遍历的思想为：首先访问根结点，然后遍历左子树，最后遍历右子树（根->左->右）；重复这个操作，直到全部访问。
代码实现：

def qianxu(now, result=[]):    
	if now == None:
		return result    
	result.append(now.data)    
	qianxu(now.left, result)    
	qianxu(now.right, result)    
	return result

对于上面这个实例，前序遍历的结果为：
[‘A’, ‘B’, ‘D’, ‘E’, ‘C’, ‘F’, ‘G’]

中序遍历

中序遍历的思想为：首先遍历左子树，然后访问根节点，最后遍历右子树（左->根->右）；重复这个操作，直到全部访问。
代码实现：

def zhongxu(now, result=[]):
    if now == None:
        return result
    (now.left, result)
    result.append(now.data)
    zhongxu(now.right, result)
    return result

对于上面这个实例，中序遍历的结果为：
[‘D’, ‘B’, ‘E’, ‘A’, ‘F’, ‘C’, ‘G’]

后序遍历

后序遍历的思想为：首先遍历左子树，然后遍历右子树，最后访问根节点（左->右->根）；重复这个操作，直到全部访问。
代码实现：

def houxu(now, result=[]):
    if now == None:
        return result
    houxu(now.left, result)
    houxu(now.right, result)
    result.append(now.data)
    return result

对于上面这个实例，后序遍历的结果为：
[‘D’, ‘E’, ‘B’, ‘F’, ‘G’, ‘C’, ‘A’]