当矩阵先验未知时如何进行补全？

矩阵补全问题

从应用背景说起

矩阵补全问题非常常见，本文列举三方面例子来说明：

1. 推荐系统。大家应该都有过网上购物或刷视频的经历，在我们使用某个APP一段时间后，打开就会发现APP好懂自己，推荐的恰好是自己想买或者想看的东西。第$i$行，第$j$列的元素代表第$i$个用户对第$j$个物品\视频的喜爱程度，那么如何知道第$i$个用户对剩下没有评分的物品\视频的喜爱程度呢？其背后的机理也可以抽象成一个矩阵补全问题。
2. 图像补全。家里如果有老旧照片，由于保管不当，或者出现了熊孩子导致照片出现裂痕或者被画笔涂抹。或是上面有当时拍摄的时间，现在我们想要把图像进行修复。而计算机中图像的存储通常将图像离散成像素点以后，以矩阵形式进行存储，灰色图像使用单通道存储，矩阵每个元素的值对应该点的灰度值。而彩色图像则采用三个通道进行存储颜色信息。在计算机中对图像进行修复就等价于对这些未知像素值的区域的像素值进行恢复。所以也转化成了一个矩阵补全问题。
3. 药物作用关系预测。在生物制药领域，通常需要通过大量的实验来探索某种药物对蛋白质或氨基酸的影响。如果使用一个矩阵来记录这种影响情况，不同行代表不同的药物，不同列代表不同的蛋白质或氨基酸。其中矩阵的元素值用来表示影响情况，那么我们在做了一部分实验的情况下，如何预测剩下的还没做实验的影响情况呢？这也是一个矩阵补全问题。

矩阵补全问题形式化及分析

矩阵补全问题可以抽象为，已知${\mathbf{X}}^{\ast }{\mid }_{\Omega }$的值，其中$\Omega$即为我们观测到的矩阵元素的位置集合。那么能否根据这个信息来找到${\mathbf{X}}^{\ast }{\mid }_{\overline{\Omega }}$的值。

显然，如果我们对原本的矩阵性质一无所知，那么我们就可以以任意值填充到矩阵未知值处。但是这样的填充显然是毫无意义的，放到实际问题中就是在随机推荐物品，在被涂抹图像处生成一堆噪点，药物关系也是随便预测。因此，对于这个问题如果要做有意义的恢复，我们通常需要知道$\mathbf{X}^*\ $的一些性质。对此，学者研究抽象了现有数据的一些特性并提出了一系列先验，例如在推荐系统中，用户之间的行为具有相似性，表现在矩阵中就是不同的行之间存在相关性，用矩阵的语言来刻画就是矩阵是低秩的；在图像中，图像相邻像素或者图像块之间具有相似性；许多自然信号在傅里叶或小波变换下，能量集中在几个基底上，呈现出了一种稀疏性；基于这些对矩阵的先验假设，涌现出了大量的算法和理论研究，对矩阵的可恢复性进行了探讨，相关文献见[1,2]引言部分。

那么问题来了，假如，任意给你一个矩阵，你不知道它是个什么来头，你该如何补全它？看似我们又回到了最开始的问题，这个问题的答案是我们无法补全。但是，如果将矩阵的先验限制在之前所提的低秩、相似和稀疏的框架下，但我们不清楚该矩阵具体是属于哪一种先验。在这个假设下，这个问题又变得有可能解决了，因为我们有可能从部分观测中来推测出整体的先验。再基于整体的先验进行矩阵补全。但是目前的工作都是聚焦于已知某一种先验或某几种先验的组合，如何设计算法或建立理论分析。而最新AIR-Net的工作则为这种矩阵先验未知的情形提供了解决方案[2]，接下来，我们就来一起看看这项工作是如何做到这一点的吧。

AIR-NET: Adaptive and Implicit Regularization neural network for matrix completion

正如名字所示，这项工作借助的工具为Net (Neural Network)，而且是一个很轻量级的Net，如同空气一般，所以叫做AIR-Net。其中全称中提到了Adaptive(自适应)和Implicit(隐式) Regularization(正则)，我们将会在下文中分别进行介绍其作用。首先，让我们再回顾一遍，我们要解决的问题：给定一个缺失的矩阵，我们知道它的先验是低秩、自相似、稀疏中的一个或多个的组合，但是不知道具体是哪些，那么我们能否根据部分观测来推测整体先验，进而进行补全？ 我们接下来将会论述无论是Adaptive还是Implicit都是让模型具备捕获上述先验的能力，但是不强制矩阵拥有上述先验中的某一个。假如我们给定的矩阵是一个评分矩阵，实际上这个矩阵的行和列都是可以任意交换位置而不影响其语义信息的，但是如果我们将一些图像矩阵的先验(如图像块的相似性和局部光滑性)加在这个上面，就其实反而带来了不好的补全效果。所以我们希望我们提出的方法，既可以拥有捕获先验的能力，又不会强行加一些不适合的先验在给定矩阵上。

Implicit regularization

说到implicit regularization，可能先要岔开矩阵补全的话题，来到神经网络。神经网络在众多任务上取得了良好的效果是有目共睹的，从理论上让人惊讶的地方在于，其参数量会远远大于数据的数量但是却不会过拟合。这在传统的拟合中是难以理解的，例如在多项式拟合中，当我们的多项式阶数远大于拟合点数时，我们是可以完全拟合这些点的。但是这种拟合结果，往往会将许多噪声都拟合进来，导致在给定数据点外该曲线无法很好表征数据，即泛化性能差。而神经网络里面却出现了一个神奇的现象，即当参数量远大于训练点数量时，学习到的神经网络具有良好的泛化性能。为了解释这个现象，出现了一系列工作，其中一类工作就是从隐式正则角度出发，对神经网络良好泛化性进行解释。其中有一个深度矩阵分解[3]的工作就讨论了深度矩阵分解具有隐式低秩的特性，即使用梯度下降优化以下式子时，会隐式收敛到一个低秩的矩阵。
$$\underset{W_1,W_2,\dots ,W_L}{\min }{\Vert \prod _{i=1}^L{W}_i-X^{\ast }\Vert }_{\Omega }$$
这和已有的矩阵分解的方法很相似，但是已有的矩阵分解方法通常$L=2$且$W_1$和$W_2$共享的维度$r$是要和我们恢复的矩阵$X^{\ast }$相匹配的。但是，我们在不知道$X^{\ast }$是否具有低秩特性时，如何选取$r$是一个难点。所幸有了深度矩阵分解，其隐式低秩正则使得我们无需选择$r$，所有矩阵的共享维度都可以选的很大即可。其次是深度矩阵分解强大的表达能力，使得最后表征的矩阵不局限于低秩。当$X^{\ast }$不具备低秩特性时，如果通过原本限制共享维度的矩阵分解的方法，表征的矩阵秩至多为$r$，和真实的$X^{\ast }$会存在差距，而借用深度矩阵分解则不会出现这种情况。这正呼应了我们之前所提的，AIR-Net既拥有表征先验的能力，但又不会强制表征某种先验。

Adaptive regularization

如果我们使用深度矩阵分解对$X^{\ast }{\mid }_{\Omega }$进行矩阵补全，那么我们就已经可以对可能具有低秩特性的矩阵进行补全了。但是往往实际的数据中，矩阵不仅仅有低秩的特性，例如图像还存在自相似性，那么我们能否对其进行表示呢？[1]就将全变分正则项和深度矩阵分解进行结合，向模型中加入了光滑性的先验，在图像恢复中取得了很好的效果，如图1所示。

但这种方法是已知数据是图像的前提下进行的，类似的，[4]向深度矩阵分解中加入了迪利克雷能量项，使用拉普拉斯矩阵来表征矩阵中行列的相关性，但是在缺失情况下，这个矩阵往往是未知的。那么我们能否提出一个正则项，能够额外加入之前提到的相似性先验，但是无需事先知道矩阵的相似性情况呢？AIR-Net中提出的自适应正则很好的解决了这一需求，原文模型如下：

其中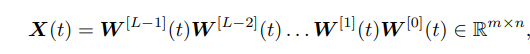

让我们来解读一下该模型，首先，(1)中的第一项即之前所讨论的深度矩阵分解。而第二项求和形式其实可以涵盖所有之前提到的相似性，首先我们将${\mathcal{T}}_i(X)$整个视为一个矩阵，而${\mathcal{R}}_{W_i}=tr({\mathcal{T}}_i(X{)}^{\top }L(W_i){\mathcal{T}}_i(X))$则是用来度量${\mathcal{T}}_i(X)$列之间相似性的，称为迪利克雷能量。其中拉普拉斯矩阵$L$文中使用以$W$为参数的神经网络进行参数化，在优化模型(1)的迭代过程中是变化的。特别的，当${\mathcal{T}}_i(X)=X$时，我们即在捕获$X$列之间的相似性，当${\mathcal{T}}_i(X)=X^{\top }$时，我们在捕获$X$行之间的相似性，而当${\mathcal{T}}_i(X)=\left[\mathrm{vec}(\mathrm{block}(\mathbf{X}){)}_1,\mathrm{vec}(\mathrm{block}(\mathbf{X}){)}_2,\dots ,\mathrm{vec}(\mathrm{block}(\mathbf{X}){)}_{n_i}\right]$时，其中$\mathrm{vec}(\mathrm{block}(\mathbf{X}){)}_j\in {\mathbb{R}}^{m_i}$是$X$中的第$j$个块按行向量化的结果。那么这种情况就可以捕获矩阵块之间的相似性。在文章中还讨论了这种自适应的正则究竟会学到什么样的拉普拉斯矩阵，理论分析表明只有当矩阵中确实存在相似性时，才会学到相似。即加入的正则项也同样有着这样的性质：拥有表征先验的能力，但只在矩阵确实具有该先验时才显露。

实验结果

矩阵补全的恢复效果

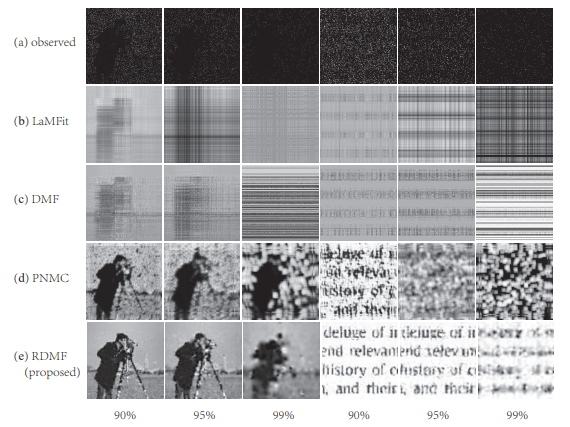
有了上述模型(1)，我们使用梯度下降法就可以对模型进行优化。最终得到的$X$即我们所求的需要补全的矩阵。那么我们来看一看矩阵的补全效果究竟如何？是否像之前所说的那样，能够在矩阵先验未知的时候对矩阵进行补全。为此我们选取了和我们介绍矩阵补全应用时相对应的三个例子进行实验。首先，我们可以看到，从数值上来看，和已有的较通用的算法如KNN,SVD,DMF，有较大的比较优势，和一些针对具体数据设计的方法如PNMC,RDMF,DMF+DE相比，除了数值大多更优，还有着更强的数据适应能力。

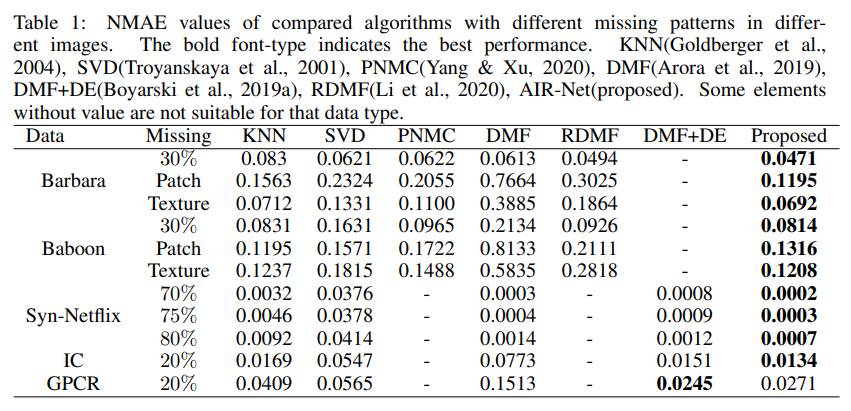
特别的，我们还给出了不同算法在不同的缺失方式的图像上的恢复效果对比，结果表明我们提出的方法在不同的缺失方式下也有着很强的适应性。

AIR-Net的防止过拟合能力

进一步，我们还探究了AIR-Net相比起DMF的防止过拟合的能力，可以从图中看到，使用了所提自适应正则的DMF显著提升了防止过拟合的能力。

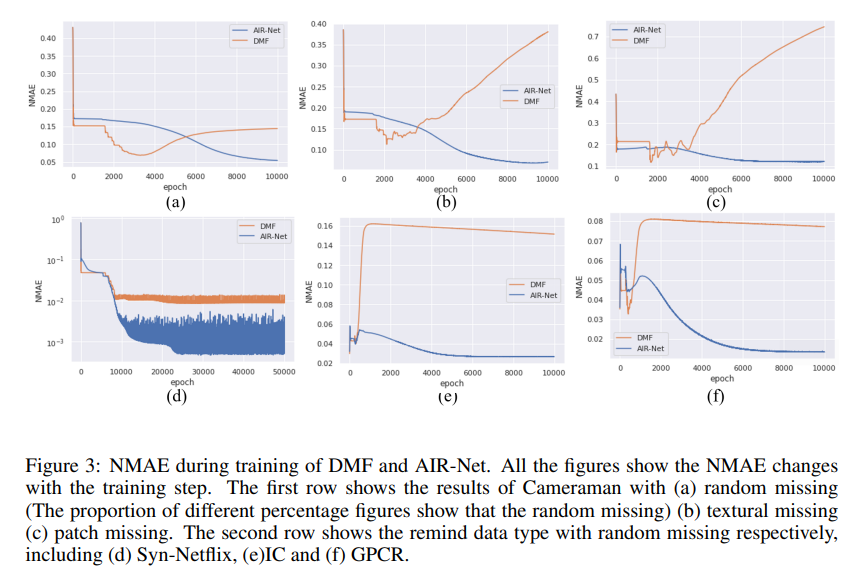
AIR-Net学到了什么

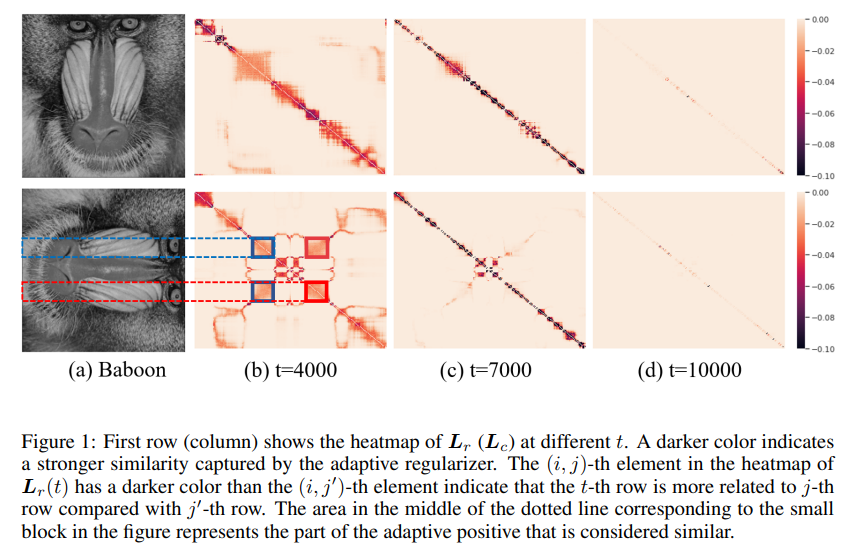
[2]号称所提出的自适应正则是可以自适应学到矩阵中的相似性的，那么是否真如它所说呢？下图给出了在Baboon上自适应正则所捕获到的拉普拉斯矩阵(不同列表示不同迭代步数)。第一行为行之间的相关关系，第$(i,j)$个元素，代表图像中第$i$行和第$j$行的相关关系，颜色越红代表相关关系越大。而第二行则为列之间的相关关系。不难观测到，在$t=4000$时，自适应正则成功捕获到了图像中眼睛所在的两列之间的相关性。随着迭代步数的增加，自适应正则认为相关的行数和列数逐渐减少，即将能量集中在高度相关的部分。在$t=7000$时，其实和全变分是很相似的，全变分就是使用每个像素点周围的像素进行补全，而这里能够自适应捕捉到这一特征，说明了我们方法的有效性。特别的，我们的方法比起全变分还多了非局部的特性，如在$t=4000$时捕获的眼睛所在列之间的相似性，就并不是相邻的像素点之间的关系。特别的，我们发现在$t=10000$时，捕获的拉普拉斯矩阵又趋向于零矩阵，这是AIR-Net的一个很好的特性。在传统的加显式正则的方法中，通常会面临 saturation issue，即最后这个显式正则不为零带来了偏差，而AIR-Net的这一性质将会避免这一问题。

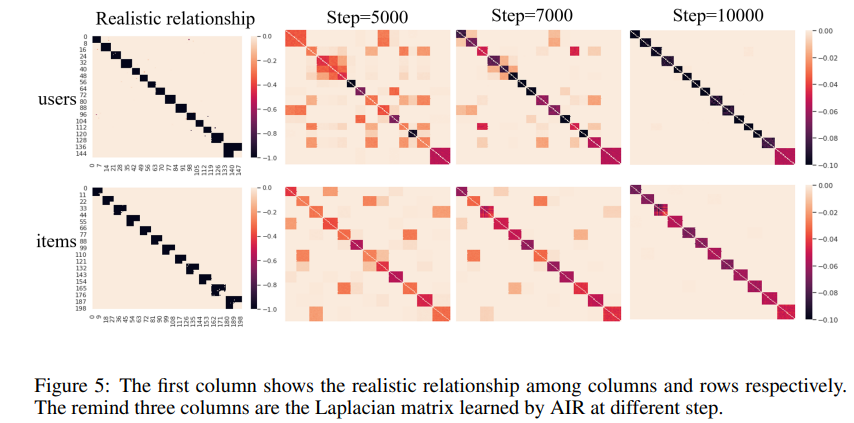
进一步我们还在推荐系统上观测了拉普拉斯矩阵的自适应学习情况。我们将学到的拉普拉斯矩阵和[4]给出的数据对应的拉普拉斯矩阵做了对比，发现我们学出的拉普拉斯矩阵和给出的拉普拉斯矩阵高度相似。证明了我们方法的有效性。

总结

总的来说，我们介绍了AIR-Net，其目标为在矩阵有可能为矩阵先验为低秩和自相似情况下如何从不完备矩阵捕获到矩阵的具体先验，然后反作用用来恢复矩阵。其在实际的多种数据中取得了很好的效果。进一步，如果矩阵先验可能为低秩、自相似、稀疏的组合的情况可以参照[5]进行拓展，[5]中讨论了隐式低秩和隐式稀疏组合的情况。

主要参考文献

[1]

• 文章名：A Regularized deep matrix factorized model of matrix completion for image restoration
• 文章地址：https://arxiv.org/abs/2007.14581
• 主旨内容：文章提出了一个带有正则化项的深度矩阵分解模型。特别的，对于图像补全问题，文章使用了total variation (TV)正则化项，发现就算是使用线性模型也能取得从数值指标和视觉效果均十分卓越。最后文章对这一模型良好效果的原因进行了分析。
• 关键词：矩阵补全，图像补全，低秩矩阵补全，神经网络，线性模型，非线性模型。
  [2]
• 文章名：AIR-NET: Adaptive and Implicit Regularization neural network for matrix completion
• 文章地址：http://arxiv-export-lb.library.cornell.edu/pdf/2110.07557
• 主旨内容：深度矩阵的隐式低秩特性在直接用于矩阵补全任务时表现不佳。因为低秩往往不足以很好刻画矩阵的先验。于是提出了AIR-NET，其中的自适应正则项为一个可学习的拉普拉斯正则项，用于自适应捕捉数据中的先验。特别的，我们发现在针对图像数据进行补全时，该自适应正则捕获到了类似于全变分正则的结果。
• 关键词：矩阵补全，低秩矩阵补全，神经网络，自适应正则，拉普拉斯正则。

[3] Arora, S., Cohen, N., Hu, W., & Luo, Y. (2019). Implicit Regularization in Deep Matrix Factorization. NeurIPS.
[4] Boyarski, A., Vedula, S., & Bronstein, A.M. (2019). Spectral Geometric Matrix Completion.
[5] You, C., Zhu, Z., Qu, Q., & Ma, Y. (2020). Robust Recovery via Implicit Bias of Discrepant Learning Rates for Double Over-parameterization. ArXiv, abs/2006.08857.