大数因数分解Pollard_rho 算法详解

大数因数分解Pollard_rho 算法详解

适用范围：给你一个大数n，将它分解它的质因子的乘积的形式。

P.S. 在下面的论述中会使用到Miller_rabin和快速乘法和快速幂，如果有兴趣请看另一篇博文。

不过其实你只需要知道Miller_rabin是判断一个数是否是素数。q_mul是求（a*b）% mod，q_pow是求(a^b) % mod即可。

Miller_rabin素数判断：http://blog.csdn.net/maxichu/article/details/45458569

大数分解最简单的思想也是试除法，这里就不再展示代码了，就是从2到sqrt(n)，一个一个的试验，直到除到1或者循环完，最后判断一下是否已经除到1了即可。

但是这样的做的复杂度是相当高的。一种很妙的思路是找到一个因子（不一定是质因子），然后再一路分解下去。这就是基于Miller_rabin的大数分解法Pollard_rho大数分解。

Pollard_rho算法的大致流程是 先判断当前数是否是素数（Miller_rabin）了，如果是则直接返回。如果不是素数的话，试图找到当前数的一个因子（可以不是质因子）。然后递归对该因子和约去这个因子的另一个因子进行分解。

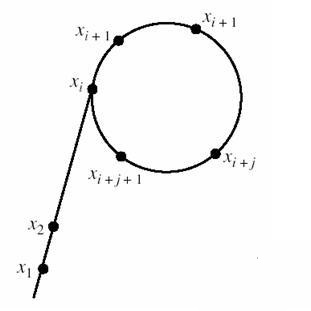
那么自然的疑问就是，怎么找到当前数n的一个因子？当然不是一个一个慢慢试验，而是一种神奇的想法。其实这个找因子的过程我理解的不是非常透彻，感觉还是有一点儿试的意味，但不是盲目的枚举，而是一种随机化算法。我们假设要找的因子为p，他是随机取一个x1，由x1构造x2，使得｛p可以整除x1-x2 && x1-x2不能整除n｝则p=gcd（x1-x2，n），结果可能是1也可能不是1。如果不是1就找寻成功了一个因子，返回因子；如果是1就寻找失败，那么我们就要不断调整x2，具体的办法通常是x2=x2*x2+c（c是自己定的）直到出现x2出现了循环==x1了表示x1选取失败重新选取x1重复上述过程。（似乎还存在一个每次找寻范围*2的优化，但是不太懂。。。）

因为x1和x2再调整时最终一定会出现循环，形成一个类似希腊字母rho的形状，故因此得名。

另外通过find函数来分解素数，如果找到了一个素数因子则加入到因子map中，否则如果用Pollard找到一个因子则递归去找素数因子。

上代码：

#include <iostream> 
#include <cstdio> 
#include <algorithm>  
#include <cmath>  
#include <cstring>  
#include <map>  
using namespace std;

const int times = 50;
int number = 0;

map<long long, int>m;
long long Random( long long n )
{
	return ((double)rand( ) / RAND_MAX*n + 0.5);
}

long long q_mul( long long a, long long b, long long mod ) //快速乘法取模
{
	long long ans = 0;
	while(b)
	{
		if(b & 1)
		{
			ans += a;
		}
		b /= 2;
		a = (a + a) % mod;

	}
	return ans;
}

long long q_pow( long long a, long long b, long long mod ) //快速乘法下的快速幂，叼
{
	long long ans = 1;
	while(b)
	{
		if(b & 1)
		{
			ans = q_mul( ans, a, mod );
		}
		b /= 2;
		a = q_mul( a, a, mod );
	}
	return ans;
}

bool witness( long long a, long long n )//miller_rabin算法的精华
{
	long long tem = n - 1;
	int j = 0;
	while(tem % 2 == 0)
	{
		tem /= 2;
		j++;
	}
	
	long long x = q_pow( a, tem, n ); //得到a^(n-1) mod n
	if(x == 1 || x == n - 1) return true;
	while(j--)
	{
		x = q_mul( x, x, n );
		if(x = n - 1) return true;
	}
	return false;
}

bool miller_rabin( long long n )  //检验n是否是素数
{

	if(n == 2)
		return true;
	if(n < 2 || n % 2 == 0)
		return false;

	for(int i = 1; i <= times; i++)  //做times次随机检验
	{
		long long a = Random( n - 2 ) + 1; //得到随机检验算子 a
		if(!witness( a, n ))  //用a检验n是否是素数
			return false;
	}
	return true;
}

long long gcd( long long a, long long b )
{
	if(b == 0)
		return a;
	return gcd( b, a%b );
}

long long pollard_rho( long long n, long long c )//找到n的一个因子
{
	long long x, y, d, i = 1, k = 2;
	x = Random( n - 1 ) + 1;
	y = x;
	while(1)
	{
		i++;
		x = (q_mul( x, x, n ) + c) % n;
		d = gcd( y - x, n );
		if(1<d&&d<n)
			return d;
		if(y == x)//找到循环，选取失败，重新来
			return n;
		if(i == k) //似乎是一个优化，但是不是很清楚
		{
			y = x;
			k <<= 1;
		}
	}
}

void find( long long n, long long c )
{
	if(n == 1)
		return;
	if(miller_rabin( n ))
	{
		m[n]++;
		number++;
		return;
	}

	long long p = n;
	while(p >= n)
		p = pollard_rho( p, c-- );
	find( p, c );
	find( n / p, c );
}

int main( )
{
	long long tar;
	while(cin >> tar)
	{
		number = 0;
		m.clear();
		find( tar, 2137342 );
		printf( "%lld = ", tar );
		if(m.empty())
		{
			printf( "%lld\n", tar );
		}
		for(map<long long, int>::iterator c = m.begin(); c != m.end();)
		{
			printf( "%lld^%d", c->first, c->second );
			if((++c) != m.end())
				printf( " * " );
		}
		printf( "\n" );
	}
	return 0;
}