推荐系统论文阅读笔记（一）Wide & Deep Learning for Recommender Systems

wide and deep 模型的核心思想是结合线性模型的记忆能力（memorization）和 DNN 模型的泛化能力（generalization），在训练过程中同时优化 2 个模型的参数，从而达到整体模型的预测能力最优。

1. Wide&Deep模型介绍

wide部分，也就是广义线性模型，广泛用于大规模的回归和分类问题。一般：线性模型 + 特征交叉

1. 优点是具有较强的记忆能力，并且可解释性很强
2. 缺点是泛化能力弱，需要通过大量的特征工程工作【由人来实现】来提高模型的泛化能力。

deep部分，也就是深度神经网络模型。

1. 优点是只需要少量的特征工程就可以有较强的泛化能力，能够发现未知的特征组合。一般来说，会将初始的高维度的稀疏特征向量通过Embedding方法转化成低维度的稠密特征向量。
2. 缺点是当用户-商品交互行为比较稀疏且排名较高的时候，通过Embedding方法转化的低维度稠密特征向量作为神经网络的输入很容易产生过拟合的情况。

记忆能力Memorization趋向于更加保守，推荐用户之前有过行为的items。相比之下，泛化能力generalization更加趋向于提高推荐系统的多样性（diversity）。

wide&deep模型则是将上述两个模型的优点结合起来，兼具记忆能力和泛化能力。

其模型图如下：

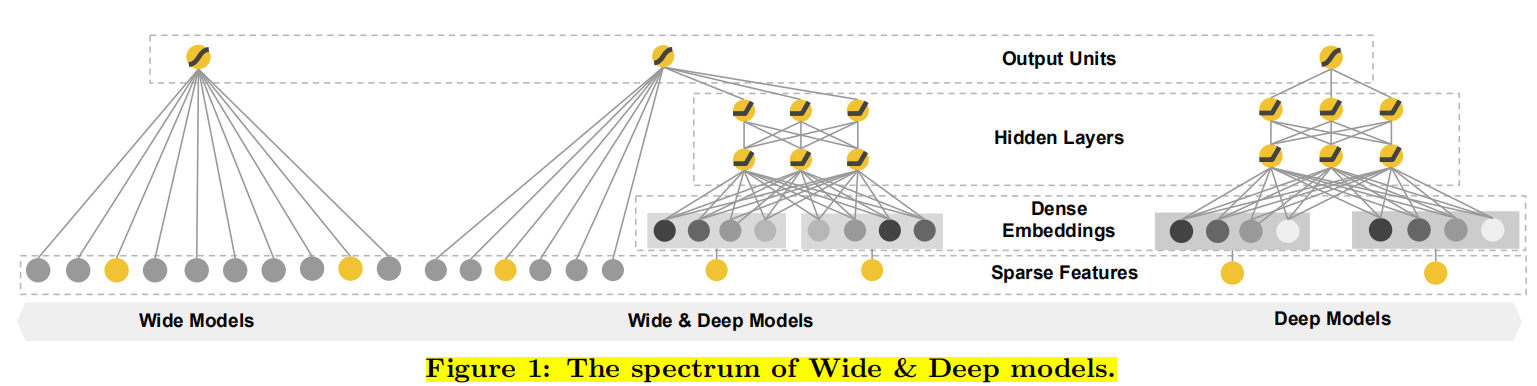
2. Wide&Deep模型框架

2.1 Wide模型——广义线性模型——记忆能力

Wide部分如上图是$y=w^{T}x+b$的广义线性模型。输入特征可以是连续特征，也可以是稀疏的离散特征，离散特征之间进行交叉后可以构成更高维的离散特征。线性模型训练中通过 L1 正则化，能够很快收敛到有效的特征组合中。最重要的转换之一是交叉乘积转换，定义为

$ \Large \phi_{k}(\mathbf{x})=\prod_{i=1}^{d} x_{i}^{c_{k i}} \quad c_{k i} \in{0,1} $

$C_{ki}$是一个布尔变量，其取值为：如果第i个特征是第k个变换${\varphi }_k$的一部分则为1，其它为0。对于二值特征，一个组合特征当原特征都为1的时候才会1（例如“性别=女”且“语言=英语”时，AND（性别=女，语言=英语）=1，其他情况均为0），这捕获了二元特征之间的相互作用，并为广义线性模型增加了非线性。

Wide部分的作用是让模型具有较强的“记忆能力”。“记忆能力”可以被理解为模型直接学习并利用历史数据中物品或者特征的“共现频率”的能力。一般来说，协同过滤、逻辑回归等简单模型有较强的“记忆能力”。由于这类模型的结构简单，原始数据往往可以直接影响推荐结果，产生类似于“如果点击过A，就推荐B”这类规则式的推荐，这就相当于模型直接记住了历史数据的分布特点，并利用这些记忆进行推荐。

举例说明：

假设在推荐模型的训练过程中，设置如下组合特征：｛user_installed_app=netflix,impression_app=pandora｝(简称netflix&pandora),它代表用户已经安装了netflix这款应用，而且曾应用商店曾经将pandora应用推送给用户看过。如果以“最终是否安装pandora”为数据标签(label)，则可以轻易地统计出netflix&pandora这个特征和安装pandora这个标签之间的共现频率。假设二者的共现频率高达10%（全局的平均应用安装率为1%），这个特征如此之强，以至于在设计模型时，希望模型一发现有这个特征，就推荐pandora这款应用（像一个深刻的记忆点一样印在脑海中），这就是所谓的**模型的“记忆能力”。**像逻辑回归这类简单模型，如果发现这样的“强特征”，则其相应的权重就会在模型训练过程中被调整得非常大，这样就实现了对这个特征的直接记忆。

2.2 Deep模型——深度神经网络——泛化能力

deep 端对应的是 DNN 模型，每个特征对应一个低维的实数向量，称之为特征的 embedding。DNN 模型通过反向传播调整隐藏层的权重，并且更新特征的 embedding。

首先对于类别特征，比如对于类别型特征，首先需要将这些高维稀疏特征 转换成低维稠密的embedding向量。随机初始化embedding向量，然后在模型训练中最小化最终损失函数。这些低维稠密向量馈送到前向传递中的神经网络的隐藏层中。 具体来说，每个隐藏层执行以下计算：

$a^{(l+1)}=f\left(W^{(l)}{a}^{(l)}+b^{(l)}\right)$

l是层数，f是激活函数，通常使用RELU函数，$a^l,b^{}$