目录
Kullback–Leibler and Jensen–Shannon Divergence
为什么Wasserstein比JS或KL Divergence更好?
生成对抗网络(GAN)在许多的用于复制真实世界中的丰富内容的生成式任务中取得了极为卓著的效果,如图片、语言和音乐。它起源于一个游戏理论:两个模型,一个生产者和一个审核者,它们互相竞争从而使得它们同时变得更好。然而,训练一个GAN模型是一个比较困难的事情,在训练时容易不稳定或者发生崩溃。
这里我将基于生成对抗网络中的一些数学知识,来解释为什么难以训练,并介绍一种GAN的改进版本来试图解决这个训练问题
Kullback–Leibler and Jensen–Shannon Divergence
在开始了解GAN之前,引入两个用于评价两个概率分布之间相似度的指标:KL散度和JS散度
(1)KL (Kullback–Leibler) 散度用于衡量概率分布p与概率分布q的偏差程度(以p为基准)
当且仅当时,
取得最小值
可以看到KL散度是非对称的。如果p(x)接近0,而q(x)显著非0,q的影响会被忽略。当我们想衡量两个同样重要的分布之间的相似性时,这可能会导致错误的结果
(1)JS散度是另一种用于衡量两个概率分布之间的相似度的指标,值域在[0, 1]。JS散度是对称的且更平滑。
一些人认为认为,GAN取得巨大成功的一个原因是将损失函数从传统最大似然方法中的不对称KL散度转换为对称JS散度。

生成对抗网络
GAN包含两个模型:
一个鉴别器D,用于估计给定样本来自真实数据集的概率。它像一个鉴定专家,经过优化可以分辨样本的真假
一个生成器G,给定一个噪声输入z(z带来潜在的输出多样性),输出合成的样本。它被训练来捕获真实的数据分布,以便其生成样本尽可能真实,或者换句话说,可以欺骗鉴别器以提供高概率。
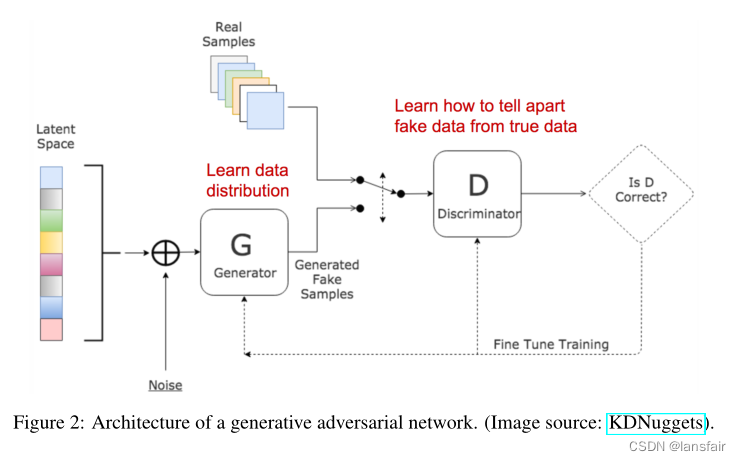
这两个模型在训练过程中相互竞争:生成器G努力欺骗鉴别者,而鉴别器模型D努力不被欺骗。这两个模型之间有趣的零和博弈促使两者改进其功能。
鉴于

一方面,我们希望通过最大化来确保生成器D对真实数据的复制是准确的;同时,给定假样本
,期望判别器通过最小化
使得输出的概率
接近0
结合以上两方面,D和G在玩一个极小极大游戏,我们应该优化以下损失函数
其中在梯度更新时对G没有影响
D的最佳值是多少?
现在我们有一个定义明确的损失函数。让我们首先检查D的最佳值是什么
考虑D为何值时使得L最小,令
积分内部的内容可写为(因为x是在所有的可能值上采样的,所以我们可以安全地忽略积分):
因此,令,我们就可以得到鉴别器的最佳值为:
一旦生成器被训练到最佳状态,Pg就非常接近Pr。当Pg=Pr时,。
什么时候全局最优?
当G和D都处于最佳值时,由上得到Pg=Pr和 ,损失函数变为
损失函数代表什么?
根据上文中列出的JS公式,Pr和Pg之间的偏差可计算为
因此,
本质上来说,当鉴别器最佳时,GAN的损失函数通过JS散度来衡量了生成器Pg与真实采样分布Pr之间的相似度,当最佳生成器复制真实数据分布,使得损失函数
最小,即
,与上述等式一致。
GAN的变种:在不同的环境中或为不同的任务而设计的GAN有许多变体。例如,对于半监督学习,一个想法是更新鉴别器以输出真实的类标签,1,…,K−1,以及一个假类标签K。生成器模型旨在欺骗鉴别器输出小于K的分类标签。
GAN的问题
尽管GAN在现实主义图像生成方面取得了巨大成功,但训练并不容易;已知该过程缓慢且不稳定
难以实现纳什均衡(Nash Equilibrium)
《Improved techniques for training gans》讨论了GAN基于梯度下降的训练过程中的问题。同时训练两个模型,以找到两人非合作博弈的纳什均衡。然而,每个模型都独立更新自身,而不考虑游戏中的其他玩家。因此同时更新两个模型的梯度不能保证收敛。
让我们看一个简单的例子,以更好地理解为什么在非合作博弈中很难找到纳什均衡。假定其中一个玩家控制以使得
最小,而同时另一玩家更新
使得
最小。
由于,
,因此在每轮迭代中我们同时用
更新
,用
更新
,
表示学习率。一旦
和
异号,每次后续的梯度更新都会导致巨大的振荡,并且不稳定性会随着时间的推移而恶化,如图所示。

低维的支持集

《Towards principled methods for training generative adversarial
networks.》讨论了Pr和Pg的support在低维流形上的问题,以及它对GAN训练的不稳定性的影响。
许多现实世界的数据集的维度,如Pr所代表的,看起来只是人为的高。它们被发现集中在一个较低维度的流形中。这实际上是流形学习的基本假设。考虑现实世界的图像,一旦主题或包含的对象被固定下来,图像就有很多限制要遵循,例如,狗应该有两只耳朵和一条尾巴,摩天大楼应该有一个笔直高大的身体,等等。这些限制使图像远离了拥有高维自由形式的可能性。
Pg也位于一个低维流形中。每当生成器给定一个小的维度(如100维)的噪声变量输入z,要求输出一个更大的图片(如64x64),在这4096个像素上的颜色分布已经被100维的小随机数向量所定义,很难填补整个高维空间。
因为Pg和Pr都位于低维流形中,所以它们几乎肯定是不相交的(见下图)。当它们具有不相交的support时,我们总是能够找到一个完美的鉴别器,该鉴别器能够100%正确地区分真假样本。

梯度消失
当判别器完美时,我们可以保证 。因此损失函数L快下降到零,我们最终没有梯度来更新学习迭代中的损失。下图展示了一个实验,当判别器变得更好时,梯度快速消失。
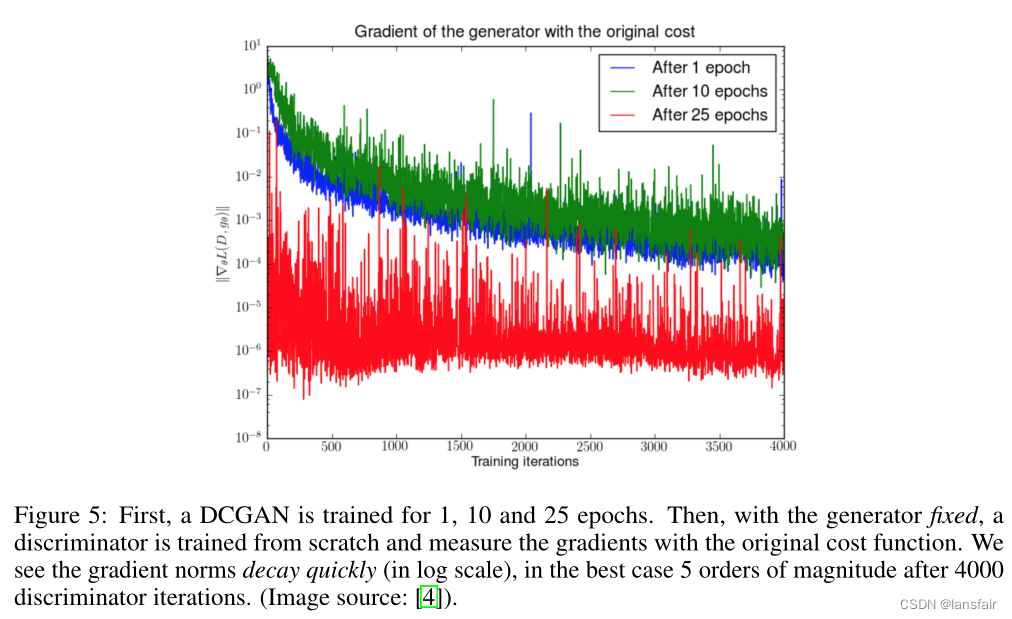
因此,训练GAN面临两难境地:
- 如果判别器表现不佳,则生成器没有准确的反馈,并且损失函数不能代表现实。
- 如果判别器做得很好,损失函数的梯度就会下降到接近零,学习就会变得非常慢,甚至被卡住。
这种困境显然能够使GAN训练变得非常困难。
Mode Collapse(模式坍塌)
在训练时,生成器可能会崩溃到始终产生相同的样本。这是GAN的常见故障情况,通常称为模式坍塌。尽管生成器可能能够欺骗相应的鉴别器,但它无法学习表示复杂的真实世界数据分布,而是陷入了一个种类极少的小空间。

缺乏恰当的评价指标
生成对抗网络天生就不具备能够告知我们训练进度的优秀反函数。而没有一个好的评估指标,这就像是在黑暗中工作。没有好的迹象表明何时停止;没有好的指标来比较多个模型的性能。
提升GAN的训练
以下建议将有助于稳定并提升GAN的训练
前五种方法是实现GAN训练快速收敛的实用技术(来自《Improved techniques for training gans》)。最后两个是在《Towards principled methods for training generative adversarial
networks》中提出的,用于解决不相交分布的问题。
(1)特征匹配
特征匹配有助于优化判别器,以检查生成器的输出是否与真实样本的预期统计数据相匹配。在这种情况下,新的损失函数定义为,其中
可以是特征(这里的特征指判别器的中间层激活值)的任何统计数据,例如平均值或中值。
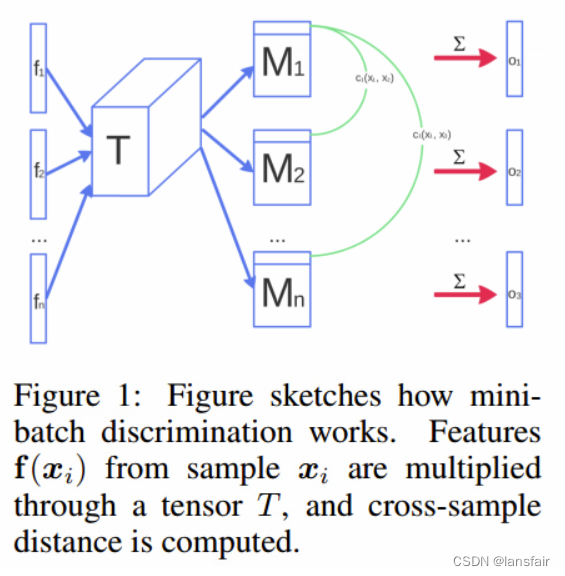
(2)小批量判别
通过小批量判别,判别器能够在一个批次中消化训练数据点之间的关系,而不是独立地处理每个点。
在一个小批量迭代中,我们计算每对样本之间的相似度,并通过将一个数据点与同批其他样本的相似度求和,即
,然后将
显式添加到模型的输入中
(3)历史平均值
对两个模型,在损失函数中加入,其中
是模型的参数,
是参数在过去的训练时间
的参数,当
在时间上变化太大时,该附加项会惩罚训练速度。
(4)单侧标签平滑
当给判别器反馈时,不要提供1和0标签,而是使用一个更soft的值,如0.9和0.1。事实证明,它可以减少网络的脆弱性。
(5)虚拟批标准化
每个数据样本都是基于一个固定的批次(“reference batch”)的数据而不是在其minibatch内进行标准化(normalized)。reference batch在开始时选择一次,并在训练过程中保持不变。
(6)增加噪声
由于Pr和Pg在高维空间中是不相交的,这就造成了梯度消失的问题。为了人为地 "分散 "分布,并为两个概率分布的重叠创造更多的机会,一种解决办法是在判别器D的输入上添加连续噪声。
(7)使用更好的相似度判别指标
vanilla GAN的损失函数衡量Pr和Pg的分布之间的JS散度。当两个分布不相交时,这个指标无法提供一个有意义的值。提议用Wasserstein度量代替JS发散,因为它有一个更平滑的值空间。
Wasserstein GAN (WGAN)
什么是 Wasserstein Distance?
Wasserstein距离是对两个概率分布之间距离的测量。它也被称为 “搬运工距离”,简称EM距离,因为通俗来说,它就是把概率分布想象成一堆石子,如何移动一堆石子,通过最小的累积移动距离把它堆成另外一个目标形状。该成本被量化为:移动的石子堆x移动距离。
举一个离散概率分布的简单例子。例如,假设我们有两个分布P和Q,每个分布都有四堆石子,并且都有石子总数都为十。每个土堆中的石子的数量分配如下,P1 = 3, P2 = 2, P3 = 1, P4 = 4; Q1 = 1, Q2 = 2, Q3 = 4, Q4 = 3。
为了使P看起来像Q,如图所示,我们做如下移动
- 首先将2个石子从P1移到P2 => (P1, Q1) 相同。
- 然后将2个石子从P2移到P3 => (P2, Q2)相同。
- 最后将1个石子从Q3移到Q4=>(P3,Q3)和(P4,Q4)相同。
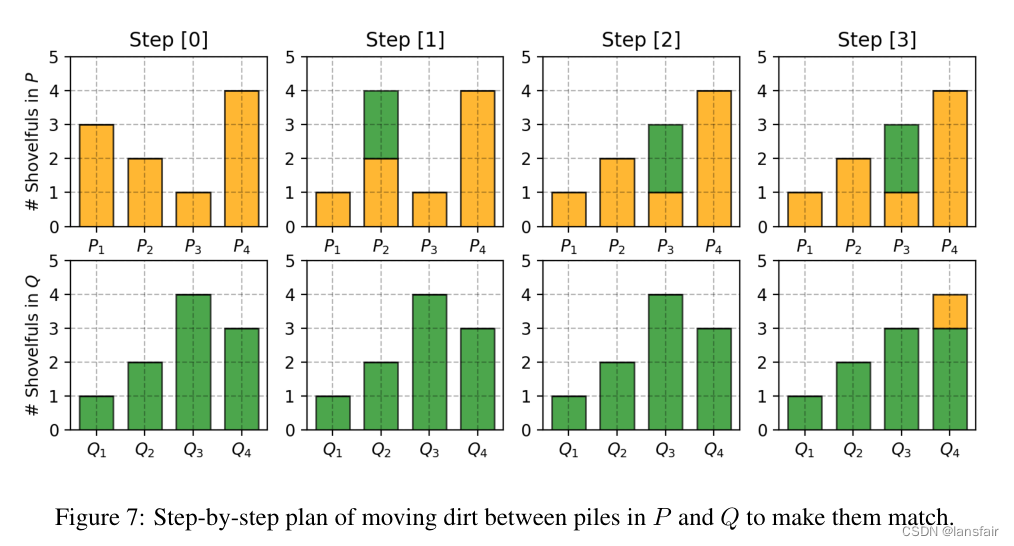
如果我们把使和
匹配所付出的成本标记为
,则有
,而在例子中
因此搬运工距离为
扩展到连续概率域,距离公式为:
在上述公式中,代表Pr和Pg所有可能的联合概率分布,一个联合分布
描述了一个石子运输计划,正如上述的离散分布例子一样,但是它位于连续的概率空间。确切来说,
表示应将石堆百分比从x点输送到y点,以使x遵循y的相同概率分布。这就是为什么在x上的边缘概率分布之和等于Pg,
(一旦我们完成了将所有可能的x移动到目标y的石子移动计划,我们最终可以根据Pg得到
的确切值),反之亦然,
当将作为起点,将
作为终点时,移动的石子总量为
,移动距离为
,因此成本为
。所有
的期望成本可以很容易地计算为:
最后,我们将所有石子移动解决方案的成本中最小的一个作为EM距离。
在瓦瑟斯坦距离的定义中,inf(infimum,也称为*最大下限*)表示我们只关注最小的成本。
为什么Wasserstein比JS或KL Divergence更好?
即使当两个分布位于没有重叠的低维流形中时,Wasserstein距离仍然可以提供一个有意义的、平滑的距离表示。
WGAN的论文用一个简单的例子说明了这一想法。
假设我们有两个概率分布,和
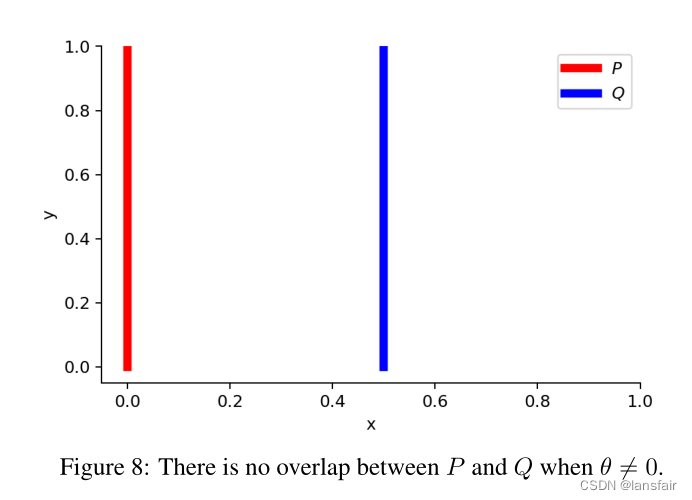
当时有:
但是当时,两个分布完全重叠时:
当两个分布不相交时,为无穷大。当
时,
值突变,在这里不可微。只有Wasserstein度量提供了一个平滑的度量,这对于使用梯度下降的稳定学习过程非常有帮助。
使用Wasserstein距离作为GAN损失函数
很难穷尽中的所有可能的联合概率分布来计算
,因此,作者提出了一个基于Kantorovich-Rubinstein对偶的公式的巧妙转换:
其中sup(上确界)与inf(下确界)相反;我们想测量最小上界,或者更简单地说,最大值。
Lipschitz连续性
要求新形式的Wasserstein度量中的函数满足
,这意味着它应该是K-Lipschitz连续的。
K-Lipschitz连续的:对于一个实数域函数,如果存在一个实数
,使得对于所有的
,都有
,那么称该函数f为K-Lipschitz连续的。
这里K被称为函数的Lipschitz常数。处处连续可微的函数是Lipschitz连续的,因为导数是有界的(估计为
)。然而,Lipschitz连续函数可能不是处处可微的,例如
解释瓦瑟斯坦距离公式的转换是如何发生的,这本身就值得一篇长篇文章,所以我跳过了这里的细节。如果您对如何使用线性规划计算瓦瑟斯坦度量,或者如何根据Kantorovich Rubinstein对偶将瓦瑟斯坦测度转换为对偶形式感兴趣,请阅Wasserstein损失函数读《Wasserstein GAN and the Kantorovich-Rubinstein Duality》
Wasserstein损失函数
假设这个函数f来自K-Lipschitz连续函数族,,由
参数化。在改进的Wasserstein GAN中,“判别器”模型基于可学习的
以找到良好的
,并且损失函数被用于衡量Pr和Pg之间的Wassertein距离:
因此,“判别者”不再直接判断是否是假样本和真样本。相反,它被训练学习K-Lipschitz连续函数,以帮助计算Wasserstein距离。随着训练中损失函数的减小,Wasserstein距离变小,生成器模型的输出变得更接近真实数据分布。
一个大问题是在训练期间保持的K-Lipschitz连续性,以使一切顺利。本文提出了一个简单但非常实用的技巧:在每次梯度更新后,将权重w裁剪在一个小窗口中,例如[−0.01,0.01],得到紧凑的参数空间
,因此
获得其下界和上界以保持Lipschitz连续性。

与原始GAN算法相比,WGAN进行了以下更改:
- 每次对判别器进行梯度更新后,将权重限制在一个小的固定范围内
-
使用从瓦瑟斯坦距离导出的新损失函数,不再使用对数。“判别器”模型不是直接的判定者,而是评估真实数据和生成数据分布之间的瓦瑟斯坦度量。
-
根据经验,作者建议判别器使用RMSProp优化器,而不是基于动量的优化器,如Adam,这可能会导致模型训练的不稳定性。关于这一点,我还没有看到明确的理论解释
遗憾的是,Wasserstein GAN并不完美。即使是WGAN论文的作者也提到,“使用权重裁剪来强制满足Lipschitz连续显然是一种糟糕的方式”。WGAN仍然存在训练不稳定、权重裁剪后收敛缓慢(裁剪窗口过大时)和渐变消失(裁剪窗口太小时)的问题。
《Improved training of wasserstein gans》中讨论了一些改进,用梯度惩罚精确地取代了权重裁剪。




















 1199
1199











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








