Courese2-第二周：优化算法

Mini-Batch

Batch梯度下降法：同时处理整个训练集。

Mini-batch梯度下降法：每次同时处理的单个的mini-batch X(t)和Y(t)，而不是同时处理全部的X和Y的训练集。

随机梯度下降法：每个样本都是独立的mini-batch。

缺点：

1. Batch梯度下降法：一次性处理整个训练集，当训练数量巨大时，单次迭代耗时太长。
2. 随机梯度下降法：丢失了所有向量化带来的加速，一次性只能处理一个训练样本，效率低下。

所以选择mini-batch：一方面得到大量的向量化，另一方面不需要等待整个训练集被处理完就可以开始进行后续工作。

指数加权移动平均数(Exponentially weighted averages)

计算趋势的话，如温度的局部平均值，或者说移动平均值。

关键方程：$v_t=\beta v_{t-1}+(1-\beta ){\theta }_t$，β∈[0, 1]

其中,$V_t表示第t天的移动平均值$。
$V_{t-1}表示第t-1天的移动平均值$。
${\theta }_t表示第t天的实际观察值$。

计算时，可视$v_t$大概是$\frac{1}{1-\beta }$的每日温度，如β=0.9，这是十天的平均值。

当高值的β：曲线要平坦一些，因为多平均了几天的温度，所以曲线波动更小，更加平坦。缺点：曲线进一步右移，指数加权平均公式在温度变化时，适应地更缓慢一些，会出现一定的延迟。

当低值的β：由于平均的数据太少，所以得到的曲线有更多的噪声，可能出现异常值，但这个曲线能够更快适应温度变化。

---

Question：到底需要平均多少天的温度？

Answer：我们平均了大约$\frac{1}{1-\beta }$天的温度。

---

执行过程：

V_theta = 0
Repeat{
    Get Next theta_t
    V_theta := β*V_theta + (1 - β)* theta_t
}

指数加权平均数公式的好处之一：它占用极少的内存，电脑内存中只占用一行数字而已。其效率，基本上只占用一行代码。

指数加权平均的偏差修正(Bias correction in exponentially weighted averages)

偏差修正：让平均数运算更加准备。

$v_t=\beta v_{t-1}+(1-\beta ){\theta }_t$，β∈[0, 1]

使用上述方程进行运算时，V0 = 0，计算V1、V2时，不能很好地估测这一年前两天的温度。通常会比正确值低很多，为了让估测变得更好。特别在估测初期，也就是不用$V_t$，而是用$\frac{V_t}{1-{\beta }^t}$，其中t就是现在的天数。随着t增加，${\beta }^t$接近于0，所以当t很大的时候，偏差修正几乎没有作用。

$eg：当t=2,1-{\beta }^t=1-0.98^2=0.0396$，因此对第二天温度的估测变成了$\frac{V_2}{0.0396}=\frac{0.0196{\theta }_1+0.02{\theta }_2}{0.0396}$，即${\theta }_1和{\theta }_2$的加权平均数，并去除了偏差。

动量梯度下降法(Gradient descent with Momentum)

基本的想法：计算梯度的指数加权平均数，并利用该梯度更新你的权重。

Gradient descent example：

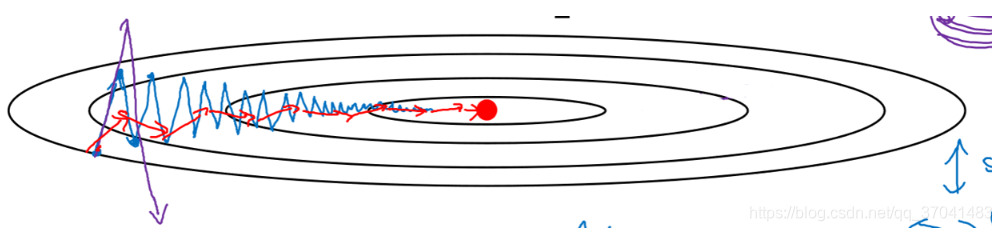
开始梯度下降算法（蓝色线），会发现其慢慢摆动到最小值，这种上下波动减慢了梯度下降法的速度。但你又无法使用更大的学习率，因为如果使用较大的学习率（紫色线），结果可能会偏离函数的范围，为了避免摆动过大，要用一个较小的学习率。

所以在纵轴上，希望学习慢一点，因为不想要这些摆动，但在横轴上，希望加快学习，希望快速从左移向右，移向最小值即红点。所以使用动量梯度下降法。

在每次迭代中，需要计算微分dW, db。我们通过计算$V_{dw}=\beta V_{dw}+(1-\beta )dW$，获得dW的移动平均数，同理得到$V_{db}$，然后重新赋值权重，$W:=W-\alpha V_{dw}$，同理$b:=b-\alpha V_{db}$，这样就可以减缓梯度下降的幅度。

Momentum算法在此：

Vdw = 0, Vdb = 0  # 零向量
On iteration t:
    Compute dW, db on the current mini-batch
    Vdw = β * Vdw + (1 - β) * dW
    Vdb = β * Vdb + (1 - β) * db
    W := W - α * Vdw
    b := b - α * Vdb
Hyperparameters:α、β     β常用值 = 0.9
学习率α、参数β控制着指数加权平均数

可以想象Momentum项(Vdw、Vdb)相当于速度，你拿了一个球，dW, db即微分项给了这个球一个加速度，此时球正向山下滚，球因为加速度越滚越快，又因为β稍小于1，相当于表现出了一些摩擦力，所以球不会无限加速下去。

你会发现这些纵轴上的摆动平均值接近于零，所以在纵轴方向，你希望放慢一点，平均过程中，正负数相互抵消，所以平均值接近于零。

在横轴方向，所有的微分都指向横轴方向，因此横轴方向的平均值仍然较大。

用算法几次迭代后，会发现动量梯度下降法，最终纵轴方向的摆动变小了，横轴方向运动更快。

RMSprop(root mean square prop)

假设纵轴代表参数b，横轴代表参数W，可能有$W_1,W_2$或者其他参数，为便于理解，被称为b和W。

RMSprop算法可以实现：减缓b方向的学习，即纵轴方向，同时加快，至少不是减缓横轴方向的学习。

RMSprop算法在此：

On iteration t:

Compute dW, db on current Mini-batch

$S_{dw}=\beta S_{dw}+(1-\beta )(dW{)}^2$

$S_{db}=\beta S_{db}+(1-\beta )(db{)}^2$

$W:=W-\alpha \frac{dW}{\sqrt{S_{dw}}}$

$b:=b-\alpha \frac{db}{\sqrt{S_{dw}}}$

这里一直把纵轴和横轴方向分别称为b和W，但实际中，你会处于参数的高维度空间，所以需要消除摆动的垂直维度，你需要消除摆动，实际上是参数W1，W2等的合计，水平维度可能W3，W4等。实际上dW是一个高维度的参数向量，db也是一个高维度的参数向量。

Adam优化算法(Adam optimization algorithm)

Adam优化算法基本上就是将Momentum和RMSprop结合在一起。

思路：

1.首先初始化$V_{dw}=0,S_{dw}=0,V_{ab}=0,S_{ab}=0$

2.在第t次迭代中，计算微分，用当前的mini-batch计算dW, db，一般会用mini-batch梯度下降法。

3.接下来，计算Momentum指数加权平均数。$V_{dw}={\beta }_1{V}_{dw}+(1-{\beta }_1)dW$，$V_{db}={\beta }_1{V}_{db}+(1-{\beta }_1)db$

4.接着用RMSprop进行更新。$S_{dw}={\beta }_2{S}_{dw}+(1-{\beta }_2)(dW{)}^2$，$S_{db}={\beta }_2{S}_{db}+(1-{\beta }_2)(db{)}^2$

5.一般使用Adam算法时，要计算偏差修正。$V_{dW}^{corrected}=\frac{V_{dW}}{1-{\beta }_1^t}$，$V_{db}^{corrected}=\frac{V_{db}}{1-{\beta }_1^t}$

S也要使用偏差修正，$S_{dW}^{corrected}=\frac{S_{dW}}{1-{\beta }_2^t}$，$S_{db}^{corrected}=\frac{S_{db}}{1-{\beta }_2^t}$

6.最后更新权重。(如果只是使用Momentum，用$V_{dw}$或修正后的$V_{dw}$，但现在加入了RMSprop的部分，所以要除以修正后$S_{dw}的平方根加上\epsilon$) $W:=W-\frac{\alpha V_{dW}^{corrected}}{\sqrt{S_{dW}^{corrected}}+\epsilon }$，$b:=b-\frac{\alpha V_{db}^{corrected}}{\sqrt{S_{db}^{corrected}}+\epsilon }$

---

Adam optimization algorithm：

首先初始化：$V_{dw}=0,S_{dw}=0,V_{ab}=0,S_{ab}=0$

On iterator t:

Compute dW, db, using mini-batch

$V_{dw}={\beta }_1{V}_{dw}+(1-{\beta }_1)dW$，$V_{db}={\beta }_1{V}_{db}+(1-{\beta }_1)db$

$S_{dw}={\beta }_2{S}_{dw}+(1-{\beta }_2)(dW{)}^2$，$S_{db}={\beta }_2{S}_{db}+(1-{\beta }_2)(db{)}^2$

$V_{dW}^{corrected}=\frac{V_{dW}}{1-{\beta }_1^t}$，$V_{db}^{corrected}=\frac{V_{db}}{1-{\beta }_1^t}$

$S_{dW}^{corrected}=\frac{S_{dW}}{1-{\beta }_2^t}$，$S_{db}^{corrected}=\frac{S_{db}}{1-{\beta }_2^t}$

$W:=W-\frac{\alpha V_{dW}^{corrected}}{\sqrt{S_{dW}^{corrected}}+\epsilon }$，$b:=b-\frac{\alpha V_{db}^{corrected}}{\sqrt{S_{db}^{corrected}}+\epsilon }$

Hyperparameters choice:

在使用Adam时，一般使用缺省值即可，如下:

$\alpha :$ need to be tune

${\beta }_1:0.9$

${\beta }_2:0.999$

$\epsilon :10^{-8}$

Question：为什么叫做Adam算法？

Answer：Adam代表Adaptive Moment Estimation(自适应矩估计)，${\beta }_1$用于计算微分(dW)，叫做第一矩，${\beta }_2$用来计算平方数的指数加权平均数$(dW{)}^2$，叫做第二矩。

学习率衰减

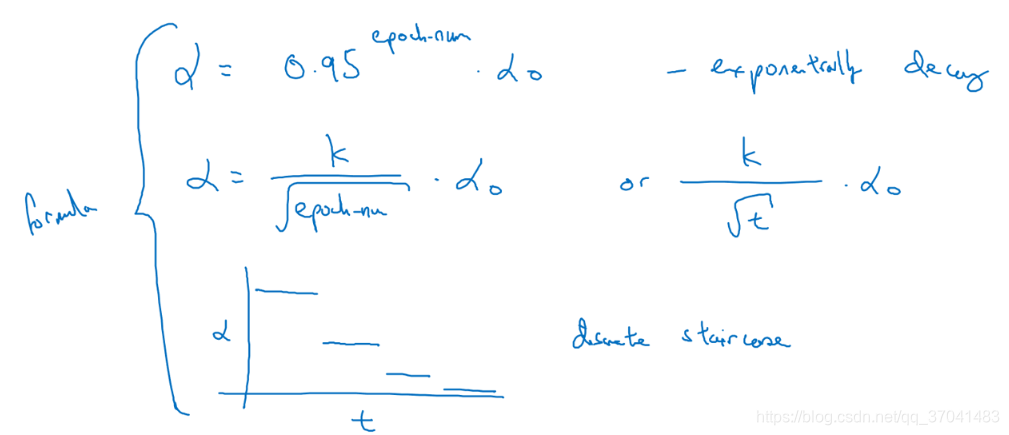
Question: 为什么要计算学习率衰减?

Answer: 若使用mini-batch梯度下降法，在迭代过程中会有噪音（蓝色），下降朝向最小值，但不会精确地收敛，算法最后在附近摆动，并不会真正收敛。所以慢慢减小学习率α地话，在学习初期，你能承受较大的步伐，但当开始收敛的时候，小一些的学习率能让你步伐小一些，所以最后你的曲线（绿色）会在最小值附近的一小块区域摆动，而不是在训练过程中，大幅度在最小值附近摆动。

mini-batch，第一次遍历训练集叫做第一代，第二次叫做第二代，以此类推。

学习率$\alpha =\frac{1}{1+decayrate\ast epochnum}{a}_0$，其中decay-rate为衰减率，epoch-num为代数，$a_0$为初始学习率。

衰减率是另一个需要调整的超参数。

Other learning rate decay methods

局部最优的问题

事实上，如果要创建一个神经网络，通常梯度为零的点并不是图中的局部最优点（左图），实际上成本函数的零梯度点，通常是鞍点（右图）。
(attachment:image.png)]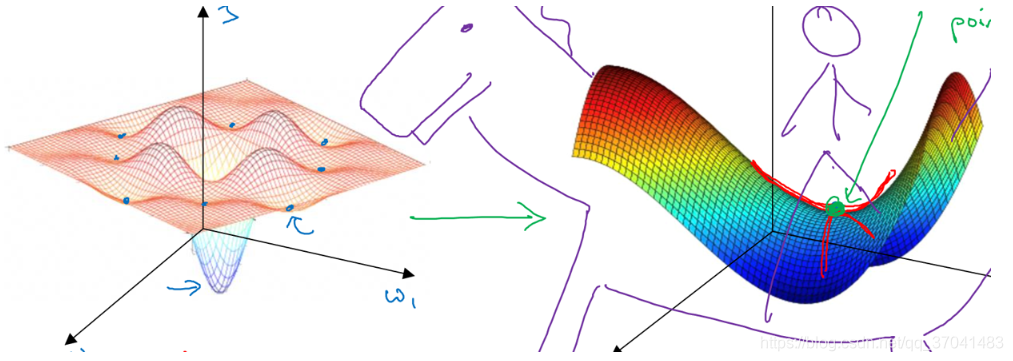
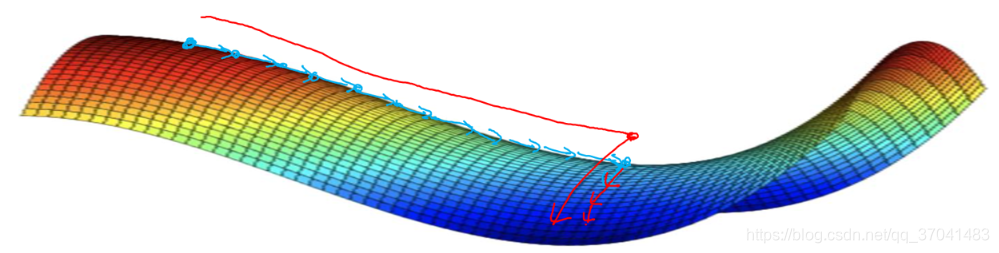
局部最优不是问题，问题是：你会花很长时间慢慢抵达平稳段的这个点。因为平稳段会减缓学习，平稳段是一块区域，其中导数长时间接近于0，若你在此处，梯度会从曲面从上向下下降，因为梯度等于或接近0，曲面很平坦，所以会花很长时间抵达平稳段这个点，又因为左边或右边的随机扰动，算法能够走出这个平稳段。

要点

1. 在训练较大的神经网络，存在大佬参数，且成本函数J被定义为在较高的维度空间时，不太可能困在极差的局部最优中。
2. 平稳段使得学习十分缓慢。在这些情况下，需要更成熟的优化算法，如Adam算法，加快速度，尽早走出平稳段。