【通俗理解】Gibbs自由能就像是一个“能量货币”，它衡量了系统在特定条件下（等温、等压、粒子数不变）能够“花费”多少能量去做非体积功，比如化学反应中的化学键形成或断裂。

【通俗理解】Gibbs自由能是如何推导并应用的？
——从定义到关键公式

【核心结论】
Gibbs自由能是热力学中的一个重要概念，它描述了系统在等温、等压、等粒子数条件下做非体积功的能力，是判断系统反应方向的重要依据。

【通俗解释】
Gibbs自由能就像是一个“能量货币”，它衡量了系统在特定条件下（等温、等压、粒子数不变）能够“花费”多少能量去做非体积功，比如化学反应中的化学键形成或断裂。当Gibbs自由能降低时，系统就倾向于发生某种变化，就像人们倾向于花费更少的钱去完成某件事情一样。

【表格】Gibbs自由能的关键概念和公式

概念/公式	描述	表达式/解释	备注
Gibbs自由能定义	系统在等温、等压、等粒子数条件下的热力学势	$G=-k_{B}T\ln Z(N,P,T)$	$Z$是配分函数，$k_B$是玻尔兹曼常数
配分函数	描述系统微观状态数量的函数	$Z(N,P,T)=\int e^{-\beta H-\beta PV}dV$	$\beta =\frac{1}{k_{B}T}$，$H$是哈密顿量
物理量计算	通过Gibbs自由能计算其他物理量	$S=-\frac{\partial G}{\partial T}$	熵
		$V=\frac{\partial G}{\partial P}$	体积
		$\mu =\frac{\partial G}{\partial N}$	化学势
重要公式	Gibbs自由能等于单粒子化学势之和	$G=N\mu$	适用于粒子数可变的系统
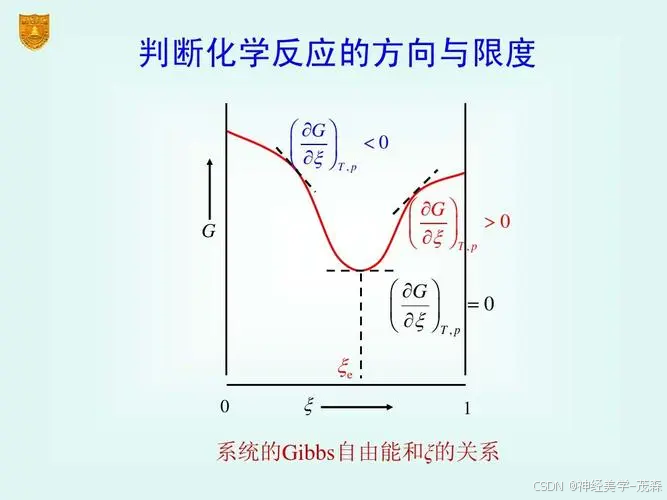
应用	判断反应方向	$\Delta G<0$反应自发进行	$\Delta G$是反应前后Gibbs自由能的变化量

关键点关系描述：

1. Gibbs自由能定义：Gibbs自由能是描述系统在等温、等压、等粒子数条件下热力学状态的物理量，它可以通过配分函数来计算。
2. 配分函数：配分函数是描述系统微观状态数量的函数，它考虑了系统中所有可能的状态，并通过玻尔兹曼因子进行加权求和。
3. 物理量计算：通过Gibbs自由能，我们可以计算出系统的其他物理量，如熵、体积和化学势。这些物理量在描述系统的热力学性质时非常重要。
4. 重要公式：Gibbs自由能等于单粒子化学势之和，这个公式在粒子数可变的系统中特别有用，它揭示了Gibbs自由能与化学势之间的紧密联系。
5. 应用：Gibbs自由能在判断反应方向方面有重要应用。当反应前后的Gibbs自由能变化量$\Delta G$小于0时，反应会自发进行。这是热力学第二定律的一个重要应用。

参考文献：

1. Atkins, P. W., & de Paula, J. (2010). Atkins’ Physical Chemistry. Oxford University Press. [【经典教材，详细讲解了物理化学的基本原理，包括Gibbs自由能等概念】]
2. Callen, H. B. (1985). Thermodynamics and an Introduction to Thermostatistics. John Wiley & Sons. [【该书深入浅出地介绍了热力学和统计热力学的基本概念，对Gibbs自由能有详细的阐述】]

Keywords：
#Gibbs自由能 #热力学势 #配分函数 #物理量计算 #化学势 #反应方向 #热力学第二定律