Cubist Artwork
| Time Limit: 1000MS | Memory Limit: 65536K | |
| Total Submissions: 398 | Accepted: 261 |
Description
International Center for Picassonian Cubism is a Spanish national museum of cubist artworks, dedicated to Pablo Picasso. The center held a competition for an artwork that will be displayed in front of the facade of the museum building. The artwork is a collection of cubes that are piled up on the ground and is intended to amuse visitors, who will be curious how the shape of the collection of cubes changes when it is seen from the front and the sides.
The artwork is a collection of cubes with edges of one foot long and is built on a flat ground that is divided into a grid of one foot by one foot squares. Due to some technical reasons, cubes of the artwork must be either put on the ground, fitting into a unit square in the grid, or put on another cube in the way that the bottom face of the upper cube exactly meets the top face of the lower cube. No other way of putting cubes is possible.
You are a member of the judging committee responsible for selecting one out of a plenty of artwork proposals submitted to the competition. The decision is made primarily based on artistic quality but the cost for installing the artwork is another important factor. Your task is to investigate the installation cost for each proposal. The cost is proportional to the number of cubes, so you have to figure out the minimum number of cubes needed for installation.
Each design proposal of an artwork consists of the front view and the side view (the view seen from the right-hand side), as shown in Figure 1.
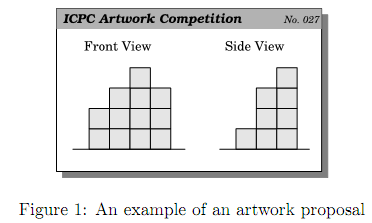
The front view (resp., the side view) indicates the maximum heights of piles of cubes for each column line (resp., row line) of the grid.
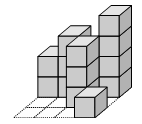
There are several ways to install this proposal of artwork, such as the following figures.

In these figures, the dotted lines on the ground indicate the grid lines. The left figure makes use of 16 cubes, which is not optimal. That is, the artwork can be installed with a fewer number of cubes. Actually, the right one is optimal and only uses 13 cubes. Note that, a single pile of height three in the right figure plays the roles of two such piles in the left one.
Notice that swapping columns of cubes does not change the side view. Similarly, swapping rows does not change the front view. Thus, such swaps do not change the costs of building the artworks.
For example, consider the artwork proposal given in Figure 2.
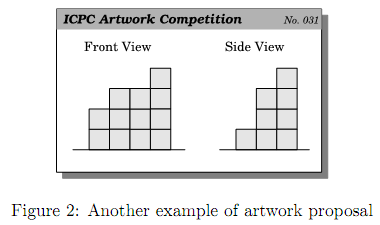
An optimal installation of this proposal of artwork can be achieved with 13 cubes, as shown in the following figure, which can be obtained by exchanging the rightmost two columns of the optimal installation of the artwork of Figure 1.
The artwork is a collection of cubes with edges of one foot long and is built on a flat ground that is divided into a grid of one foot by one foot squares. Due to some technical reasons, cubes of the artwork must be either put on the ground, fitting into a unit square in the grid, or put on another cube in the way that the bottom face of the upper cube exactly meets the top face of the lower cube. No other way of putting cubes is possible.
You are a member of the judging committee responsible for selecting one out of a plenty of artwork proposals submitted to the competition. The decision is made primarily based on artistic quality but the cost for installing the artwork is another important factor. Your task is to investigate the installation cost for each proposal. The cost is proportional to the number of cubes, so you have to figure out the minimum number of cubes needed for installation.
Each design proposal of an artwork consists of the front view and the side view (the view seen from the right-hand side), as shown in Figure 1.

The front view (resp., the side view) indicates the maximum heights of piles of cubes for each column line (resp., row line) of the grid.
There are several ways to install this proposal of artwork, such as the following figures.

In these figures, the dotted lines on the ground indicate the grid lines. The left figure makes use of 16 cubes, which is not optimal. That is, the artwork can be installed with a fewer number of cubes. Actually, the right one is optimal and only uses 13 cubes. Note that, a single pile of height three in the right figure plays the roles of two such piles in the left one.
Notice that swapping columns of cubes does not change the side view. Similarly, swapping rows does not change the front view. Thus, such swaps do not change the costs of building the artworks.
For example, consider the artwork proposal given in Figure 2.

An optimal installation of this proposal of artwork can be achieved with 13 cubes, as shown in the following figure, which can be obtained by exchanging the rightmost two columns of the optimal installation of the artwork of Figure 1.

Input
The input is a sequence of datasets. The end of the input is indicated by a line containing two zeros separated by a space. Each dataset is formatted as follows.
The integers w and d separated by a space are the numbers of columns and rows of the grid, respectively. You may assume 1 <= w <= 10 and 1 <= d <= 10. The integers separated by a space in the second and third lines specify the shape of the artwork. The integers h i (1 <= h i <= 20, 1 <= i <= w) in the second line give the front view, i.e., the maximum heights of cubes per each column line, ordered from left to right (seen from the front). The integers h i ' (1 <= h i ' <= 20, 1 <= i <= d) in the third line give the side view, i.e., the maximum heights of cubes per each row line, ordered from left to right (seen from the right-hand side).
w d
h1 h2 ... hw
h1' h2' ... hd'
The integers w and d separated by a space are the numbers of columns and rows of the grid, respectively. You may assume 1 <= w <= 10 and 1 <= d <= 10. The integers separated by a space in the second and third lines specify the shape of the artwork. The integers h i (1 <= h i <= 20, 1 <= i <= w) in the second line give the front view, i.e., the maximum heights of cubes per each column line, ordered from left to right (seen from the front). The integers h i ' (1 <= h i ' <= 20, 1 <= i <= d) in the third line give the side view, i.e., the maximum heights of cubes per each row line, ordered from left to right (seen from the right-hand side).
Output
For each dataset, output a line containing the minimum number of cubes. The output should not contain any other extra characters.
You can assume that, for each dataset, there is at least one way to install the artwork.
You can assume that, for each dataset, there is at least one way to install the artwork.
Sample Input
5 5 1 2 3 4 5 1 2 3 4 5 5 5 2 5 4 1 3 4 1 5 3 2 5 5 1 2 3 4 5 3 3 3 4 5 3 3 7 7 7 7 7 7 3 3 4 4 4 4 3 4 4 3 4 2 2 4 4 2 1 4 4 2 8 8 8 2 3 8 3 10 10 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 10 9 20 1 20 20 20 20 20 18 20 20 20 20 20 20 7 20 20 20 20 0 0
Sample Output
15 15 21 21 15 13 32 90 186
Source
Tokyo 2009
题意:给你一个三维图的正视图和右视图,问你能达到当前效果需要的最小的正方体个数,输入的是每个视图看到的每一列的最高高度;
思路:这题比赛的时候看了一下样例很快发现了每组的答案和输入的关系,不知道这么描述,讲一个例子:
1 2 3 4 5
3 3 3 4 5,这组样例,3,4,5只加一遍,剩下1,2,3,3每个都加一遍,也就是如果上下两行有对应相等的数,那么这个数只加一遍,剩下的所有数都加上(好好理解一下,,,这个做法回过头一想还是有一定道理的,自己在草稿纸上画一画)
AC代码:
题意:给你一个三维图的正视图和右视图,问你能达到当前效果需要的最小的正方体个数,输入的是每个视图看到的每一列的最高高度;
思路:这题比赛的时候看了一下样例很快发现了每组的答案和输入的关系,不知道这么描述,讲一个例子:
1 2 3 4 5
3 3 3 4 5,这组样例,3,4,5只加一遍,剩下1,2,3,3每个都加一遍,也就是如果上下两行有对应相等的数,那么这个数只加一遍,剩下的所有数都加上(好好理解一下,,,这个做法回过头一想还是有一定道理的,自己在草稿纸上画一画)
AC代码:
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int a[105],b[105];
int vis1[105],vis2[105];
int main()
{
int n,m;
while(~scanf("%d%d",&n,&m))
{
if(n==0&&m==0)break;
memset(vis1,0,sizeof(vis1));
memset(vis2,0,sizeof(vis2));
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
vis1[a[i]]++;//数据范围很小,记录每个数出现的次数
}
for(int i=1;i<=m;i++)
{
scanf("%d",&b[i]);
vis2[b[i]]++;
}
int sum=0;
for(int i=0;i<=20;i++)
{
int tmp1=vis1[i];
int tmp2=vis2[i];
int k=min(tmp1,tmp2);
sum+=k*i;//两个数组中相同的数字只算他们出现的相同次数遍
sum+=abs(tmp1-tmp2)*i;//再加上该数字再某个数组中多出现的次数
}
printf("%d\n",sum);
}
return 0;
}





















 2294
2294

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








