形形色色的空间填充曲线 和 L-System

最新推荐文章于 2024-08-17 08:45:02 发布
最新推荐文章于 2024-08-17 08:45:02 发布
阅读量1.3k 收藏 13
点赞数 3
分类专栏： python
原文链接：https://zhuanlan.zhihu.com/p/35358486
版权

 

已获许可，转载：形形色色的空间填充曲线 和 L-System - 邓卓的文章 - 知乎 https://zhuanlan.zhihu.com/p/35358486

注：建议使用 Python 3，本文所有代码虽然可以使用 Python2 运行，但图像实现有些缺陷

使用 Python 可以用简单的逻辑画出一些的空间填充曲线，比如下面 Hilbert 曲线、Dragon 曲线 以及 Gosper 曲线，这些曲线都可以『一笔画』画出

上面 3 种曲线的点生成算法都非常简单，不需要 import 任何库

 

# Hilbert 曲线

def _hilbert(direction, rotation, order):
    if order == 0:
        return

    direction += rotation
    _hilbert(direction, -rotation, order - 1)
    step(direction)

    direction -= rotation
    _hilbert(direction, rotation, order - 1)
    step(direction)
    _hilbert(direction, rotation, order - 1)

    direction -= rotation
    step(direction)
    _hilbert(direction, -rotation, order - 1)

def step(direction):
    next = {0: (1, 0), 1: (0, 1), 2: (-1, 0), 3: (0, -1)}[direction & 0x3]

    global x, y
    x.append(x[-1] + next[0])
    y.append(y[-1] + next[1])

def hilbert(order):
    global x, y
    x = [0,]
    y = [0,]

    _hilbert(0, 1, order)

    return (x, y)

 

当然，要将其画出来，需要额外的库。这里使用的是 Matplotlib，然后简单的使用方式是：

import matplotlib.pyplot as plt
x, y = hilbert(4);plt.plot(x, y); plt.show()

 

稍微复杂点的使用方式

import matplotlib.pyplot as plt

fig, ax = plt.subplots(1, 4)   
for i in range(4):
    sub = ax[i]
    sub.axis("off")
    sub.set_aspect("equal")
    x, y = hilbert(i + 1)
    sub.plot(x, y)
plt.show()

Dragon 曲线点生成逻辑

def _dragon_A(direction, order):
    if order == 0:
        return direction

    direction = _dragon_A(direction, order - 1)

    direction += 1
    direction = _dragon_B(direction, order - 1)

    step(direction)
    direction += 1

    return direction

def _dragon_B(direction, order):
    if order == 0:
        return direction

    direction -= 1
    step(direction)
    direction = _dragon_A(direction, order - 1)

    direction -= 1
    direction = _dragon_B(direction, order - 1)

    return direction

def step(direction):
    next = {0: (1, 0), 1: (0, 1), 2: (-1, 0), 3: (0, -1)}[direction & 0x3]

    global x, y
    x.append(x[-1] + next[0])
    y.append(y[-1] + next[1])

def dragon(order):
    global x, y
    x = [0,]
    y = [0,]

    direction = 0
    step(direction)
    _dragon_A(0, order)

    return (x, y)


Gosper 曲线点生成逻辑

def _gosper_A(direction, order):

    if order == 0:
        step(direction)
        return

    _gosper_A(direction, order - 1)

    direction -= 1
    _gosper_B(direction, order - 1)

    direction -= 2
    _gosper_B(direction, order - 1)

    direction += 1
    _gosper_A(direction, order - 1)

    direction += 2
    _gosper_A(direction, order - 1)
    _gosper_A(direction, order - 1)

    direction += 1
    _gosper_B(direction, order - 1)

def _gosper_B(direction, order):
    if order == 0:
        step(direction)
        return

    direction += 1
    _gosper_A(direction, order - 1)

    direction -= 1
    _gosper_B(direction, order - 1)
    _gosper_B(direction, order - 1)

    direction -= 2
    _gosper_B(direction, order - 1)

    direction -= 1
    _gosper_A(direction, order - 1)

    direction += 2
    _gosper_A(direction, order - 1)

    direction += 1
    _gosper_B(direction, order - 1)

cos30 = 3.0 ** 0.5 / 2.0
sin30 = 0.5
nexts = {0: (cos30, sin30), 1: (0, 1), 2: (-cos30, sin30), 3: (-cos30, -sin30), 4: (0, -1), 5: (cos30, -sin30)}
def step(direction):
    next = nexts[direction % 6]

    global x, y
    x.append(x[-1] + next[0])
    y.append(y[-1] + next[1])

def gosper(order):
    global x, y
    x = [0,]
    y = [0,]

    _gosper_A(0, order)

    return (x, y)

上面 3 种曲线的点生成算法，虽然简单，但是每一次对于一个新的曲线或者图形都要新写的一段逻辑，还是略显麻烦。实际上有一个通用的规则来描述各种曲线和图形，然后对于这个通用规则可以写一个解释器，就可以很容易的描述一个新的曲线和图形。

L-system

L-system，全称 Lindenmayer system，是一位植物学家开发的。在本文中会实现一个简单的 L-system 解释器，因为只使用部分功能，所以这个解释器只是 L-system 的一个子集

L-system 可以使用一个非常形式化的 三元组 [公式] 来定义。但估计大家应该不会对此有兴趣，如果真有兴趣的话可以参考百度百科以及维基百科。

下面我们直接通过示例，来解释 L-system

 

Gosper 曲线的 L-system

{
  "start": "A",
  "rules": {"A": "A-B--B+A++AA+B-", "B": "+A-BB--B-A++A+B"}
  "iterator: 2
}

使用一个字符串来代表 Gosper 曲线的生成过程。根据 start 知道 A 是起始字符串 str，根据 rules 中的替换规则，不断的把 str 中的 A 和 B 替换成箭头右边的字符串，替换次数为预先指定的迭代次数 iterator

第 0 次，起始 A
第 1 次 A => A-B--B+A++AA+B-
第 2 次 A-B--B+A++AA+B- => A-B--B+A++AA+B--+A-BB--B-A++A+B--+A-BB--B-A++A+B+A-B--B+A++AA+B-++A-B--B+A++AA+B-A-B--B+A++AA+B-++A-BB--B-A++A+B-

替换完成后，最后赋予字符串几何意义，代表如下意思 —— 任意设定起点和方向，从左到右扫描字符串，遇到 A / B 就前进一格，遇到 + 向左旋转 60°，遇到 - 向右旋转 60°。如此就可以得到一个 Gosper 曲线

{
  "rotate": 60,
  "actions": {"+": "left", "-": "right", "A": "forward", "B": "forward"}
}

下面我们来实现一个简单的 L-system 解释器，并验证如上的 Gosper 曲线规则

def replacement(str, rules, order):
    for i in range(order):
        dst = ""
        for s in str:
            if s in rules:
                dst += rules[s]
            else:
                dst += s
        str = dst
    return str

def interpretation(str, actions, rotate, angle, x, y):
    import math

    point_x = [x,] 
    point_y = [y,]

    for s in str:
        if s not in actions:
            continue
        if actions[s] == "left":
            angle -= rotate
        elif actions[s] == "right":
            angle += rotate
        elif actions[s] == "forward":
            r = angle / 180.0 * math.pi
            point_x.append(point_x[-1] + math.cos(r))
            point_y.append(point_y[-1] + math.sin(r))
    return point_x, point_y

验证

# Gosper 曲线
grammer = {
  "start": "A",
  "rules": {"A": "A-B--B+A++AA+B-", "B": "+A-BB--B-A++A+B"},
}

geometry = {
  "rotate": 60,
  "actions": {"+": "left", "-": "right", "A": "forward", "B": "forward"}
}

import matplotlib.pyplot as plt

fig, ax = plt.subplots(1, 4)   
for i in range(4):
    str = replacement(grammer["start"], grammer["rules"], i + 1)
    x, y = interpretation(str, geometry["actions"], geometry["rotate"], 30, 0, 0)

    sub = ax[i]
    sub.axis("off")
    sub.set_aspect("equal")
    sub.plot(x, y)

plt.show()

有了这个最基本的 L-system 解释器，我们再来画别的曲线就很容易了

# Sierpinski arrowhead 曲线
grammer = {
  "start": "A",
  "rules": {"A": "B-A-B", "B": "A+B+A"},
}

geometry = {
  "rotate": 60,
  "actions": {"+": "left", "-": "right", "A": "forward", "B": "forward"}
}

# Sierpinski triangle
grammer = {
  "start": "F-G-G",
  "rules": {"F": "F-G+F+G-F", "G": "GG"},
}

geometry = {
  "rotate": 120,
  "actions": {"+": "left", "-": "right", "F": "forward", "G": "forward"}
}

# Koch snowflake
grammer = {
  "start": "F",
  "rules": {"F": "F+F--F+F"},
}

geometry = {
  "rotate": 60,
  "actions": {"+": "left", "-": "right", "F": "forward"}
}

# Hilbert 曲线
grammer = {
  "start": "A",
  "rules": {"A": "-BF+AFA+FB-", "B":"+AF-BFB-FA+"},
}

geometry = {
  "rotate": 90,
  "actions": {"+": "left", "-": "right", "F": "forward"}
}

# Dragon 曲线
grammer = {
  "start": "FX",
  "rules": {"X": "X+YF+", "Y": "-FX-Y"},
}

geometry = {
  "rotate": 90,
  "actions": {"+": "left", "-": "right", "F": "forward"}
}

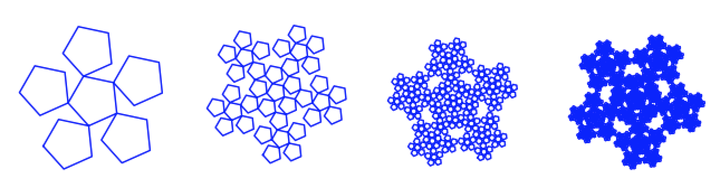
# 不知名的图形
grammer = {
  "start": "F-F-F-F-F",
  "rules": {"F": "F-F++F+F-F-F"},
}

geometry = {
  "rotate": 72,
  "actions": {"-": "left", "+": "right", "F": "forward"}
}

上面这个 L-system 实现的非常简单，只能描述『一笔画』的曲线。现在在几何意义上添加两个动作 —— 入栈 和 出栈

入栈代表将当前的 点和角度 入栈，出栈代表将当前的 点和角度 出栈，新的 L-system 如下（使用 [ 和 ] 表示这两个动作）

def replacement(str, rules, order):
    for i in range(order):
        dst = ""
        for s in str:
            if s in rules:
                dst += rules[s]
            else:
                dst += s
        str = dst
    return str

def interpretation(str, actions, rotate, angle, x, y):
    import math

    point_x = [x,] 
    point_y = [y,]
    coordinates = [[point_x, point_y],]

    stack = []
    for s in str:
        if s not in actions:
            continue
        if actions[s] == "left":
            angle -= rotate
        elif actions[s] == "right":
            angle += rotate
        elif actions[s] == "forward":
            r = angle / 180.0 * math.pi
            point_x.append(point_x[-1] + math.cos(r))
            point_y.append(point_y[-1] + math.sin(r))
        elif actions[s] == "push":
            stack.append((angle, point_x[-1], point_y[-1]))
        elif actions[s] == "pop":
            angle, _x, _y = stack[-1]
            stack = stack[:-1]

            point_x = [_x,]
            point_y = [_y,]
            coordinates.append([point_x, point_y])
            
    return coordinates
现在我们找几个示例来测试下

grammer = {
  "start": "X",
  "rules": {"X": "F+[[X]-X]-F[-FX]+X", "F": "FF"},
}

geometry = {
  "rotate": 25,
  "actions": {"-": "left", "+": "right", "F": "forward", "[": "push", "]": "pop"}
}

import matplotlib.pyplot as plt

fig, ax = plt.subplots(1, 4)   

for i in range(4):
    str = replacement(grammer["start"], grammer["rules"], i + 3)
    coordinates = interpretation(str, geometry["actions"], geometry["rotate"], 60, 0, 0)
    print(coordinates)

    sub = ax[i]
    sub.axis("off")
    sub.set_aspect("equal")
    for coordinate in coordinates: 
        x, y = coordinate
        sub.plot(x, y)

plt.show()

# 不知名植物二
grammer = {
  "start": "X",
  "rules": {"X": "F[+X]-X", "F": "FF"},
}

geometry = {
  "rotate": 25,
  "actions": {"-": "left", "+": "right", "X": "forward", "F": "forward", "[": "push", "]": "pop"}
}

# 不知名植物三
grammer = {
  "start": "FX",
  "rules": {"X": "FF+[+F]+[-F]", "F": "FF-[-F+F]+[+F-F]"},
}

geometry = {
  "rotate": 25,
  "actions": {"-": "left", "+": "right", "X": "forward", "F": "forward", "[": "push", "]": "pop"}
}

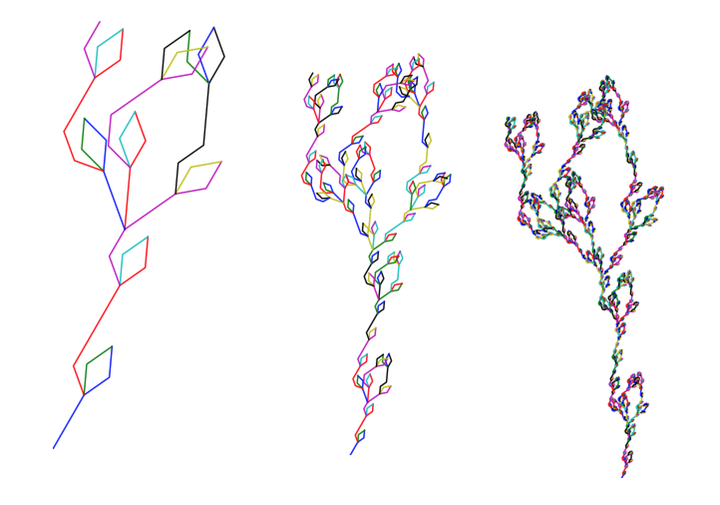
L-system 的表达能力比上面描述的要更加强大。在实践中，一个完整 L-system 实现有很实际的应用，比如园林设计。在阅读关于空间填充曲线的资料，写了一些曲线实现，后来发现一个简单的 L-system 就有很强的表达能力，觉得非常有意思，于是写了本文。后面举的例子已经不是空间填充曲线了，但同样简单，若有兴趣，可以自定义编写 grammer 和 geometry，来看下会生成什么图形

有一条鱼
关注
专栏目录
GeoHadoop 之 Hilbert 空间填充曲线 Java 实现（二）
探索地理之源 分享GIS价值
02-19 5148
承接上一节，来看下做出来的效果！
【python】生成希尔伯特曲线和摩尔曲线
ranjuese的博客
04-09 1682
最近在学习空间填充曲线，知乎上有一篇文章《形形色色的空间填充曲线》里面讲了无需使用画图库，输入曲线的阶数order，只用matplotlib就可以表现出希尔伯特曲线的方法，其得到的曲线穿过平面区域的坐标点list很有用。 生成希尔伯特曲线的代码如下： def _hilbert(direction, rotation, order): if order == 0: return direction += rotation _hilbert(direction, -ro
高斯帕曲线 Gosper curve理解与js实现
qq_21219781的博客
06-13 2791
    最近看threejs相关的知识点，发现一个 比较有趣的曲线-Gosper curve，如图所示：是由无数个基本图像组成    类似的曲线还有很多，比如龙曲线(Dragon curve)、Koch曲线(Koch curve)、摩尔定律曲线(Moore curve)、谢尔宾斯基曲线(Sierpiński curve)、奥斯古德曲线(Osgood curve)等等，这些曲线的共有特性为降维，以G...
算法笔记：空间填充曲线
最新发布
qq_40206371的博客
08-17 373
六次迭代的希尔伯特曲线：
空间填充曲线
GIS探索之路
12-12 4884
空间填充曲线 从数学的角度上看，可以将空间填充曲线看成是一种把N维空间数据转换到1维连续空间上的映射函数。实际上，存储磁盘是一维的存储设备，而空间数据是多维数据，不存在天然的一维顺序。因此，为了使空间上邻近的元素映射也尽可能是一维直线上接近的点，提出了许多的映射方法。最常用的方法包括Z Ordering、Hilbert 曲线等等。 皮亚诺曲线 希尔伯特曲线 z ordering curve S2 参考 3DTILES_bounding_volume_S2 Debug S2 in CesiumJS
Gray空间填充曲线
xugen12的专栏
09-15 3744
百度Gray编码，发现其规则如下： 1）1位格雷码有两个码字 2）(n+1)位格雷码中的前2^n个码字等于n位格雷码的码字，按顺序书写，加前缀0 3）(n+1)位格雷码中的后2^n个码字等于n位格雷码的码字，按逆序书写，加前缀1 4）n+1位格雷码的集合 = n位格雷码集合(顺序)加前缀0 + n位格雷码集合(逆序)加前缀1 而Gary填充曲线是在Gray编码的基础发展的。构造Gra
JUST技术：管理海量空间数据的利器-空间填充曲线
李瑞远-时空数据
01-25 2202
现实世界中存在大量的多维空间数据，如加油站位置、河流走向等。为了高效存储和管理海量的空间数据，很多基于Key-Value存储的空间数据库，如开源的空间插件GeoMesa[1]、京东城市自研的时空数据引擎JUST[2]，都使用了空间填充曲线技术。它们能够将多维空间数据转换到一维空间上，并通过转换后的一维空间索引值存储和查询多维数据，因此能够在Key-Value数据库中存储管理海量的时空数据。本文详细介绍了几种常用的空间填充曲线(Z曲线、Hilbert曲线、XZ-Ordering)的映射算法。 一、背景介绍
形形色色的曲线 蒋声编著 上海教育出版社
11-29
形形色色的曲线 蒋声编著 上海教育出版社 中学生文库 (共6册), 这套丛书还有 《有趣的心理学实验》,《棋盘上的数学》,《数学万花镜》,《冰川奇观》,《谈谈怎样学好数学》。
【最新】“第五空间”观后感-网络安全调查报告、网络安全整改报告.docx
06-07
虚拟空间和现实世界深度融合，面对不断涌现的各种已知和未知的网络安全威胁，我们能够找到守护人类命运共同体的密钥吗？ 在中央网信办网络安全协调局、上海市网信办的指导下，上海广播电视台融媒体中心制作的大型...
TDK Lambda-GenesysTM 3U10千瓦和15千瓦可编程电源系列增加高压型号
01-13
这类高压电源可满足 OEM、工业、国防与航天、新能源以及含半导体和汽车测试、元器件测试/老化在内的自动测试设备等各种市场上形形色色应用的需求。 　TDK-Lambda 的 Genesys:trade_mark:高压型号提供 5 年质保，...
Space_Filling_Curve 空间填充曲线经典论文
05-09
此文章是Space_Filling_Curve空间填充曲线经典论文，文章详细介绍了空间填充曲线的构建方法与索引方式
hilbertcurve:一维空间填充希尔伯特曲线和ND坐标之间的映射
05-02
目录 这是一个程序包，可在沿着一维距离h和n维点(x_0, x_1, ... x_n-1) 。 有两个重要参数， n尺寸数（必须> 0） p构造希尔伯特曲线时使用的迭代次数（必须> 0） 我们考虑边长为2^p的n维。 该超立方体包含2^{np}单位超立方体（每个维度2^p ）。 单位超立方体的数量确定了沿希尔伯特曲线的可能离散距离（从0到2^{np} - 1索引）。 快速开始 用pip安装软件包， pip install hilbertcurve 您可以沿希尔伯特曲线计算给定距离的点， >> > from hilbertcurve . hilbertcurve import HilbertCurve >> > p = 1 ; n = 2 >> > hilbert_curve = HilbertCurve ( p , n ) >> > distances = list ( ra
js画曲线功能
06-05
纯js画曲线功能，当有数据时，替换数据即可
最新人教版五年级语文下册第5单元《习作：形形色色的人》教案-.pdf
10-11
- 本次习作的主题是“形形色色的人”，要求学生从生活中选取一个特点鲜明的人物进行描绘。 - 选材应注重突出人物的独特性，可以选择小区里的人物、学校中的老师或同学等。 - 通过具体事例展现人物的特点，比如...
GeoHash与空间填充曲线
chiduokui9989的博客
11-26 1671
看了一下GeoHash，怎么看都是一个莫顿编码（Morton Code）。 而莫顿编码也是一个Z-order曲线。 空间填充曲线除了Z-order以往还有，Hilbert曲线，Peano曲线。 这些都可以用来作为把二维映射到一维的空间索引。 瓦片编码的基本要求是相邻的瓦片编码相似，这样缓存更友...
eclipse自动填充_新的Eclipse项目SFCurve：由于空间填充曲线，查询速度更快
07-01 197
SFCurve项目目前处于Eclipse Foundation的孵化器阶段，其起源于两个LocationTech项目– GeoTrellis和GeoMesa。 这两个项目都已经开发了Scala代码，可以根据数据的时空特性轻松创建和编辑Z曲线索引。 由于GeoTrellis和GeoMesa都产生了类似的代码来解决相同的问题，因此，现在的工作集中在创建公共库SFCurve上。 空间填充曲线...
探索空间填充曲线的奇妙世界：Scurve项目深度解析
gitblog_00097的博客
05-21 322
探索空间填充曲线的奇妙世界：Scurve项目深度解析 项目地址:https://gitcode.com/cortesi/scurve 在计算机科学中，空间填充曲线是一种特殊的数学构造，它以独特的方式填充二维或三维空间，拥有广泛的应用价值。今天，我们有幸向您推荐一个专注于这一领域的开源项目——Scurve，该项目不仅包含了多种空间填充曲线算法的实现，还提供了直观的可视化工具。 项目介绍 Scurve...
"交换机基础：形形色色的交换机概述和应用分析
本文主要讨论交换机基础的相关内容，包括交换机的概述、按规模应用分、按架构特点分、按传输介质和传输速度分等方面的内容。交换机是一种用于数据通信的网络设备，具有转发和过滤数据包的功能，可以提高网络效率和...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值