形式化验证
- 为什么需要形式化验证?
- 因为这种证明方法可以在理论上寻找到程序中的错误,而这些错误可能不可复现、无法被测试所覆盖、或者只会发生一次等,比如1994年奔腾芯片的FDIV错误,除法运算会发生某种偏差,这个问题是在90亿次除法运算中才可能出现1次错误,或者一些其他的著名BUG:原来曾有过这么多BUG!哪个CPU最严重。我们没用办法通过简单的测试来找到这些BUG,但通过形式化的验证却可以找到哪里可能存在问题。
- 形式化验证的三个部分:
- 用于系统建模的框架
- 用于描述待验证性质的规范语言
- 用来确定系统描述是否满足规范的验证方法
- 根据证明的依据对形式化验证的分类
- 基于证明的处理中:系统描述一组公式 Γ \Gamma Γ,他的规范是另一个公式 ϕ \phi ϕ,验证的方法就是试图找到 Γ ⊢ ϕ \Gamma \vdash \phi Γ⊢ϕ的证明。
- 基于模型的处理中(本节笔记重点):系统由适当逻辑的模型 M \mathcal{M} M表示,规范也是另一个公式 ϕ \phi ϕ表示,验证方法则是由计算模型 M \mathcal{M} M是否满足 ϕ \phi ϕ构成(写作 M ⊨ ϕ \mathcal{M} \models \phi M⊨ϕ)。
- 根据验证的完全程度对形式化验证的分类
- 性质验证:规范描述系统的单一性质。
- 完全验证:规范描述的系统的全部性质。
模型检测(Model Checking)
- 时态逻辑(Temporal Logic)
- 思想:在一个模型中,公式的真与假不是静态的,而在命题逻辑或谓词逻辑中的确如此。
- 含义:时态逻辑的模型包含若干状态,而一个公式可以在某些状态下为真,在其他状态下为假。公式可以随系统的状态演化而改变其真值。
- 模型检测:模型检测是一种自动的、基于模型的、性质验证的处理方法。
- 模型检测也是基于时态逻辑的,在模型检测中,模型
M
\mathcal{M}
M是迁移系统,性质
ϕ
\phi
ϕ是是时态逻辑公式,为了验证一个系统满足一个性质,需要三步操作:
- 使用模型检测器的描述性语言对系统进行建模,得到一个模型 M \mathcal{M} M
- 使用模型检测器的规范语言对性质进行编码,禅师一个时态逻辑公式 ϕ \phi ϕ
- 以 M \mathcal{M} M和 ϕ \phi ϕ做输入,运行模型检测器
如果模型检测器 M ⊨ ϕ \mathcal{M} \models \phi M⊨ϕ的结果为假(或者no、false),大多数模型检测器会产生导致失败的系统行为轨迹,我们称这一操作为之为逆向追踪
- 模型检测就是对问题 M , s ⊨ ϕ \mathcal{M},s \models \phi M,s⊨ϕ是否成立计算答案的过程,此处的 ϕ \phi ϕ是时态逻辑的一个公式, M \mathcal{M} M是所考虑的一个适当模型, s s s是该模型的一个状态, ⊨ \models ⊨是满足关系。
- 模型检测也是基于时态逻辑的,在模型检测中,模型
M
\mathcal{M}
M是迁移系统,性质
ϕ
\phi
ϕ是是时态逻辑公式,为了验证一个系统满足一个性质,需要三步操作:
线性时态逻辑(Linear-time Temporal Logic,简写为LTL)
- 定义:一种能表达时间概念的特殊时态逻辑。它将时间轴看成一个线性的状态序列,可以无限延伸到未来。常用来精确表示模型的动态语义。
- 计算路径(简称为路径):模型里的状态序列。因为未来是不确定的,有无数种可能,在模型中表示有无数条路径,代表未来不同的可能,任何一条路径都可能会是一条实际的路径(每一条路径都有可能发生,但只有一条路径会真正发生)。
- 命题原子公式:原子公式用 p , q , r , p 1 , q 1 , r 1 . . . p,q,r,p_1,q_1,r_1... p,q,r,p1,q1,r1...等符号表示,这些原子代表系统可能成立的事实,比如“打印机正在打印”,“进程1220被挂起”,或者“程序计数器上的值为6”。
- 原子集合:表示系统可能成立的全部事实,用 A t o m s Atoms Atoms表示,比如 p , q p,q p,q的所有组合: A t o m s = { ∅ , { p } , { q } , { p , q } } Atoms = \{\varnothing,\{p\},\{q\},\{p,q\}\} Atoms={∅,{p},{q},{p,q}}
LTL语法
ϕ : : = ⊥ ∣ ⊤ ∣ p ∣ ( ¬ ϕ ) ∣ ( ϕ ∧ ϕ ) ∣ ( ϕ ∨ ϕ ) ∣ ( ϕ → ϕ ) ∣ ( X ϕ ) ∣ ( F ϕ ) ∣ ( G ϕ ) ∣ ( ϕ U ϕ ) ∣ ( ϕ W ϕ ) ∣ ( ϕ R ϕ ) \phi ::= \perp | \top | p| (\neg \phi) | (\phi \wedge \phi)| (\phi \vee\phi)| (\phi \to \phi) | (X \phi)| (F \phi)| (G \phi)| (\phi U \phi)| (\phi W \phi)| (\phi R \phi) ϕ::=⊥∣⊤∣p∣(¬ϕ)∣(ϕ∧ϕ)∣(ϕ∨ϕ)∣(ϕ→ϕ)∣(Xϕ)∣(Fϕ)∣(Gϕ)∣(ϕUϕ)∣(ϕWϕ)∣(ϕRϕ)
上述公式表示,如果 ϕ \phi ϕ是LTL公式,则 ¬ ϕ , ( ϕ ∧ ϕ ) , ( G ϕ ) ⋯ \neg \phi, (\phi \wedge \phi), (G \phi) \cdots ¬ϕ,(ϕ∧ϕ),(Gϕ)⋯也是LTL公式,同时 ⊥ ∣ ⊤ ∣ p \perp | \top | p ⊥∣⊤∣p也是LTL公式。其中, p p p是取自原子集合 A t o m s Atoms Atoms的任意命题原子
-
时态连接词:
- 一元时态连接词:
- X X X:下一个状态。
- F F F:某未来状态。
- G G G:所有未来状态。
- 二元时态连接词:
- U U U:直到。
- R R R:释放。
- W W W:弱-直到。
- 一元时态连接词:
-
时态连接词的含义:
-
原子命题 p p p表示路径 π \pi π中第一个原子命题是 p p p
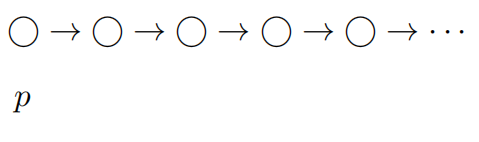
-
X p Xp Xp表示路径 π \pi π中第二个原子命题是 p p p

-
G p Gp Gp表示路径 π \pi π中每一个原子命题都是 p p p

-
p U q pUq pUq表示对于路径 π : s 0 → s 1 → ⋯ \pi:s_0 \to s_1 \to \cdots π:s0→s1→⋯中,假设原子命题 p p p在且只在 s 3 , s 4 , s 5 , s 6 , s 7 , s 8 s_3,s_4,s_5,s_6,s_7,s_8 s3,s4,s5,s6,s7,s8状态点满足,原子命题 q q q只在 s 9 s_9 s9状态点满足。则如果 i i i的值为 0 , 1 , 2 0,1,2 0,1,2, π i ⊭ p U q \pi^i \nvDash pUq πi⊭pUq(因为这个时候的开始点没有 p p p);如果 i i i的值为 3 , 4 , 5 , 6 , 7 , 8 , 9 3,4,5,6,7,8,9 3,4,5,6,7,8,9,则 π i ⊨ p U q \pi^i \vDash pUq πi⊨pUq。

-
p R q pRq pRq
q q q必须保持为真,直到 p p p为真的时刻

或者
如果 p p p为真的时刻不存在,则 q q q一直为真

R R R是 U U U的对偶,即 ϕ R ψ \phi R \psi ϕRψ等价于 ¬ ( ¬ ϕ U ¬ ψ ) \neg (\neg \phi U \neg \psi) ¬(¬ϕU¬ψ)
-
-
LTL公式范例: ( F ( p → ( G r ) ) ∨ ( ( ¬ q ) U p ) ) (F(p \to (G \ r)) \vee ((\neg q) U \ p )) (F(p→(G r))∨((¬q)U p))
语法树:
在我们书写LTL公式时,在不引起歧义的前提下,很多括号可以省略,比如 ( p → ( F q ) ) (p \to (F \ q)) (p→(F q))可以无歧义地简写为 p → F q p \to F \ q p→F q
-
语法优先级从高到低:
- 一元时态连接词: ¬ , X , F , G \neg,X,F,G ¬,X,F,G
- 二元时态连接词: U , R , W U,R,W U,R,W
- ∨ , ∧ \vee,\wedge ∨,∧
- → \to →
LTL语义
-
迁移系统: M = { S , → , L } \mathcal{M}=\{S,\to,L\} M={S,→,L}, S S S是一个状态集合; → \to →是迁移关系(这个迁移关系表示 S S S上的二元关系),使得每个属于 S S S的 s s s中(也就是 s ∈ S s \in S s∈S),有某个 s ′ s' s′满足 s → s ′ s \to s' s→s′(这个 s ′ ∈ S s' \in S s′∈S);标记函数 L → P ( A t o m s ) L \to \mathcal{P}(Atoms) L→P(Atoms)
- 迁移系统简称为模型 ,一个模型有状态集 S S S,关系 → \to →(描述的是系统如何从一个状态转向另一个状态),以及每个状态 s s s伴随有原子命题的集合 L ( s ) L(s) L(s)。我们用 P ( A t o m s ) \mathcal{P}(Atoms) P(Atoms)表示 A t o m s Atoms Atoms的幂集,也叫做原子描述集。
- 幂集范例:对于状态集 S = { p , q } S = \{p,q\} S={p,q},则他的幂集 P ( A t o m s ) = { ∅ , { p } , { q } , { p , q } } \mathcal{P}(Atoms)=\{\varnothing,\{p\},\{q\},\{p,q\}\} P(Atoms)={∅,{p},{q},{p,q}}
- 用有向图表示一个有限迁移系统
M
\mathcal{M}
M的所有信息,图的结点包含了在该状态下为真的所有原子命题。
- 模型范例:
M
\mathcal{M}
M有三个状态
s
0
,
s
1
,
s
2
s_0,s_1,s_2
s0,s1,s2,状态之间仅有的可能迁移是
s
0
→
s
1
,
s
0
→
s
2
,
s
1
→
s
0
,
s
1
→
s
2
,
s
2
→
s
2
s_0 \to s_1,s_0 \to s_2,s_1 \to s_0,s_1 \to s_2,s_2 \to s_2
s0→s1,s0→s2,s1→s0,s1→s2,s2→s2,若
L
(
s
0
)
=
{
p
,
q
}
,
L
(
s
1
)
=
{
q
,
r
}
,
L
(
s
2
)
=
{
r
}
L(s_0)=\{p,q\},L(s_1)=\{q,r\},L(s_2)=\{r\}
L(s0)={p,q},L(s1)={q,r},L(s2)={r},则将模型的信息浓缩到状态图中为:

- 模型范例:
M
\mathcal{M}
M有三个状态
s
0
,
s
1
,
s
2
s_0,s_1,s_2
s0,s1,s2,状态之间仅有的可能迁移是
s
0
→
s
1
,
s
0
→
s
2
,
s
1
→
s
0
,
s
1
→
s
2
,
s
2
→
s
2
s_0 \to s_1,s_0 \to s_2,s_1 \to s_0,s_1 \to s_2,s_2 \to s_2
s0→s1,s0→s2,s1→s0,s1→s2,s2→s2,若
L
(
s
0
)
=
{
p
,
q
}
,
L
(
s
1
)
=
{
q
,
r
}
,
L
(
s
2
)
=
{
r
}
L(s_0)=\{p,q\},L(s_1)=\{q,r\},L(s_2)=\{r\}
L(s0)={p,q},L(s1)={q,r},L(s2)={r},则将模型的信息浓缩到状态图中为:
在上述状态图中,状态 r r r是一个死锁状态,他的下一个状态永远只能是自身
-
无限路径:模型 M = { S , → , L } \mathcal{M}=\{S,\to,L\} M={S,→,L}中的一条路径是 S S S中状态的无限序列 s 1 , s 2 , s 3 , ⋯ s_1,s_2,s_3,\cdots s1,s2,s3,⋯,对每个 i ⩾ 1 i \geqslant 1 i⩾1,都有 s i → s i + 1 s_i \to s_{i+1} si→si+1,则我们可以将该路径写为 π = s 1 → s 2 → s 3 → ⋯ \pi = s_1 \to s_2 \to s_3 \to \cdots π=s1→s2→s3→⋯,我们用 π i \pi^i πi表示从第 i i i个状态开始的后缀,比如 π 3 = s 3 → s 4 → ⋯ \pi^3=s_3\to s_4 \to \cdots π3=s3→s4→⋯
- 将上面的模型范例里的系统展开成一个从特定状态开始的所有计算路径的无限树为:
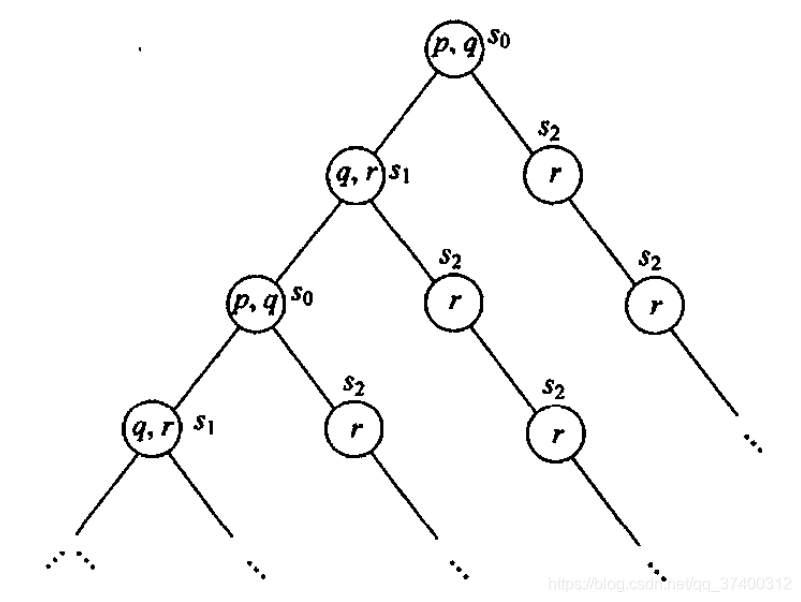
- 将上面的模型范例里的系统展开成一个从特定状态开始的所有计算路径的无限树为:
-
设 M = { S , → , L } \mathcal{M}=\{S,\to,L\} M={S,→,L}是一个模型, π = s 1 → s 2 → s 3 → ⋯ \pi = s_1 \to s_2 \to s_3 \to \cdots π=s1→s2→s3→⋯是 M \mathcal{M} M中地一条路径,路径 π \pi π与LTL公式满足关系定义如下:
- π ⊨ ⊤ \pi \vDash \top π⊨⊤
-
π
⊭
⊥
\pi \nvDash \perp
π⊭⊥
⊤ \top ⊤表示总为真的事实, ⊥ \perp ⊥表示总为假的事实
- π ⊨ p \pi \vDash p π⊨p当且仅当 p ∈ L ( s 1 ) p \in L(s_1) p∈L(s1)
- π ⊨ ϕ 1 ∧ ϕ 2 \pi \vDash \phi_1 \wedge \phi_2 π⊨ϕ1∧ϕ2当且仅当 π ⊨ ϕ 1 \pi \vDash \phi_1 π⊨ϕ1且 π ⊨ ϕ 2 \pi \vDash \phi_2 π⊨ϕ2
- π ⊨ ϕ 1 ∨ ϕ 2 \pi \vDash \phi_1 \vee \phi_2 π⊨ϕ1∨ϕ2当且仅当 π ⊨ ϕ 1 \pi \vDash \phi_1 π⊨ϕ1或 π ⊨ ϕ 2 \pi \vDash \phi_2 π⊨ϕ2
- π ⊨ ϕ 1 → ϕ 2 \pi \vDash \phi_1 \to \phi_2 π⊨ϕ1→ϕ2当且仅当只要 π ⊨ ϕ 1 \pi \vDash \phi_1 π⊨ϕ1就有 π ⊨ ϕ 2 \pi \vDash \phi_2 π⊨ϕ2
-
π
⊨
X
ϕ
\pi \vDash X \ \phi
π⊨X ϕ当且仅当
π
2
⊨
ϕ
\pi^2 \vDash \phi
π2⊨ϕ
- π ⊨ X ϕ \pi \vDash X \ \phi π⊨X ϕ表示路径从第二个状态开始满足LTL公式 ϕ \phi ϕ
- ϕ \phi ϕ是原子集内的某个原子命题,也是一个LTL公式,在路径中也叫做状态; X ϕ X \ \phi X ϕ表示这个原子命题的下一个状态; π 2 \pi^2 π2表示从路径 π \pi π上的第二个状态开始的路径
- π ⊨ G ϕ \pi \vDash G \ \phi π⊨G ϕ当且仅当对所有 i ⩾ 1 , π i ⊨ ϕ i\geqslant 1,\pi^i \vDash \phi i⩾1,πi⊨ϕ
- π ⊨ F ϕ \pi \vDash F \ \phi π⊨F ϕ当且仅存在某个 i ⩾ 1 i\geqslant 1 i⩾1使得 , π i ⊨ ϕ ,\pi^i \vDash \phi ,πi⊨ϕ
- π ⊨ ϕ U ψ \pi \vDash \phi \ U \psi π⊨ϕ Uψ当且仅当存在某个 i ⩾ 1 i\geqslant 1 i⩾1,使得 π i ⊨ ψ \pi^i \vDash \psi πi⊨ψ并且对所有 j = 1 , ⋯ , i − 1 j=1,\cdots,i-1 j=1,⋯,i−1,有 π i ⊨ ϕ \pi^i\vDash \phi πi⊨ϕ
- π ⊨ ϕ W ψ \pi \vDash \phi \ W \psi π⊨ϕ Wψ当且仅当存在某个 i ⩾ 1 i\geqslant 1 i⩾1,使得 π i ⊨ ψ \pi^i \vDash \psi πi⊨ψ且对所有的 j = 1 , ⋯ , i − 1 j=1,\cdots,i-1 j=1,⋯,i−1,有 π i ⊨ ϕ \pi^i\vDash \phi πi⊨ϕ,或者对所有 k ⩾ 1 k \geqslant 1 k⩾1,有 π k ⊨ ψ \pi^k\vDash \psi πk⊨ψ
-
π
⊨
ϕ
R
ψ
\pi \vDash \phi \ R \ \psi
π⊨ϕ R ψ当且仅当或者存在某个
i
⩾
1
i\geqslant 1
i⩾1,使得
π
i
⊨
ψ
\pi^i \vDash \psi
πi⊨ψ且对所有
j
=
1
,
⋯
,
i
j=1,\cdots,i
j=1,⋯,i,有
π
i
⊨
ψ
\pi^i\vDash \psi
πi⊨ψ;或者对所有
k
⩾
1
k \geqslant 1
k⩾1,有
π
k
⊨
ψ
\pi^k\vDash \psi
πk⊨ψ
π ⊨ ϕ R ψ \pi \vDash \phi \ R \ \psi π⊨ϕ R ψ还可以表述为:当且仅当或者 ∃ i ≥ 0 \exists i ≥ 0 ∃i≥0使得 π i ⊨ ϕ \pi^i \vDash \phi πi⊨ϕ且对于每个 j ≤ i j ≤ i j≤i都有 π j ⊨ ψ πj \vDash \psi πj⊨ψ,或者对于所有的 k ≥ 0 k \geq 0 k≥0都有 π k ⊨ ψ \pi^k \vDash \psi πk⊨ψ
-
状态满足公式:设 M = ( S , → , L ) M = (S, \to, L) M=(S,→,L)是一个模型, s ∈ S , ϕ s \in S,\phi s∈S,ϕ是一个LTL公式,若对从 s s s出发的每条路 π \pi π都有 π ⊨ ϕ \pi \vDash \phi π⊨ϕ,则称状态 s s s满足 ϕ \phi ϕ,记作 M , s ⊨ ϕ M, s \vDash \phi M,s⊨ϕ,或 s ⊨ ϕ s \vDash \phi s⊨ϕ
-
范例:

对于上面的Kripke结构,有如下结论:
-
s
0
⊨
(
p
∧
q
)
,
¬
r
,
X
r
s_0 \vDash (p \wedge q),\neg r,Xr
s0⊨(p∧q),¬r,Xr
s 0 s_0 s0这个状态满足三个条件:- ( p ∧ q ) : (p \wedge q): (p∧q): s 0 s_0 s0状态上有原子命题 p p p和 q q q
- ¬ r : \neg r: ¬r: s 0 s_0 s0状态上没有原子命题 r r r
- X r : X r: Xr: s 0 s_0 s0状态的下一个结点有原子命题 r r r
-
s
0
⊭
X
(
q
∧
r
)
s_0 \nvDash X(q \wedge r)
s0⊭X(q∧r)
s 0 s_0 s0的下一个状态不一定满足包含原子命题 q q q和 r r r。因为 s 0 s_0 s0的下一个状态如果是 s 2 s_2 s2的话,只包含原子命题 r r r而不包含原子命题 q q q,如果 s 0 s_0 s0的下一个状态如果是 s 1 s_1 s1的话才包含原子命题 q q q和 r r r -
s
0
⊨
G
¬
(
p
∧
r
)
s_0 \vDash G \neg(p \wedge r)
s0⊨G¬(p∧r)
s 0 s_0 s0这个状态满足未来所有状态不同时包含原子命题 p p p和 r r r。因为 s 0 s_0 s0以后可能要迁移到 s 1 s_1 s1、 s 2 s_2 s2或迁移回 s 0 s_0 s0,而这三个状态均不同时包含原子命题 p p p和 r r r,所以 s 0 s_0 s0这个状态满足未来所有状态不同时包含原子命题 p p p和 r r r -
s
2
⊨
G
r
s_2 \vDash G r
s2⊨Gr
s 2 s_2 s2状态满足未来所有状态全部包含原子命题 r r r -
s
⊨
F
(
¬
q
∧
r
)
→
F
G
r
s \vDash F(\neg q \wedge r)\to FGr
s⊨F(¬q∧r)→FGr
s s s状态满足,如果未来的状态不含原子命题 q q q但包含原子命题 r r r,则未来全部状态都包含原子命题 r r r。因为不含原子命题 q q q但包含原子命题 r r r的状态只有 s 2 s_2 s2, s 2 s_2 s2的下一个状态永远只能是 s 2 s_2 s2, s 2 s_2 s2也只包含原子命题 r r r,所以未来全部状态都包含原子命题 r r r
语义等价
- 定义:设 ϕ , ψ \phi,\psi ϕ,ψ是 LTL 公式, 若对于所有的模型 M \mathcal{M} M以及 M \mathcal{M} M中的所有的路 π \pi π都有 π ⊨ ψ \pi \vDash \psi π⊨ψ当且仅当 π ⊨ ψ \pi \vDash \psi π⊨ψ,则称 ϕ \phi ϕ与 ψ \psi ψ是语义等价的, 记作 ϕ ≡ ψ \phi \equiv \psi ϕ≡ψ
- 语义等价等价刻画:设 ϕ , ψ \phi,\psi ϕ,ψ是 LTL 公式,它们是语义等价的,当且仅当若对于所有的模型 M \mathcal{M} M以及 M \mathcal{M} M中的所有的状态 s s s都有 s ⊨ ϕ s \vDash \phi s⊨ϕ当且仅当 s ⊨ ψ s \vDash \psi s⊨ψ
- 等价性质:
- 对偶性:
- G ϕ ≡ ¬ F ¬ ϕ G \phi \equiv \neg F \neg \phi Gϕ≡¬F¬ϕ
- F ϕ ≡ ¬ G ¬ ϕ F \phi \equiv \neg G \neg \phi Fϕ≡¬G¬ϕ
- ϕ U ψ ≡ ¬ ( ¬ ϕ R ¬ ψ ) \phi U \psi \equiv \neg (\neg \phi R \neg \psi) ϕUψ≡¬(¬ϕR¬ψ)
- ϕ R ψ ≡ ¬ ( ¬ ϕ U ¬ ψ ) \phi R \psi \equiv \neg (\neg \phi U \neg \psi) ϕRψ≡¬(¬ϕU¬ψ)
- X ϕ ≡ ¬ X ¬ ϕ X \phi \equiv \neg X \neg \phi Xϕ≡¬X¬ϕ
- 分配性:
- F ( ϕ ∨ ψ ) ≡ F ϕ ∨ F ψ F(\phi \vee \psi) \equiv F \phi \vee F \psi F(ϕ∨ψ)≡Fϕ∨Fψ
- G ( ϕ ∧ ψ ) ≡ F ϕ ∧ F ψ G(\phi \wedge \psi) \equiv F \phi \wedge F \psi G(ϕ∧ψ)≡Fϕ∧Fψ
- 对偶性:
- 连接词相互定义
- F ϕ ≡ ⊤ U ϕ F \phi \equiv \top U \phi Fϕ≡⊤Uϕ
- G ϕ ≡ ⊥ R ϕ G \phi \equiv \perp R \phi Gϕ≡⊥Rϕ
- ϕ R ψ ≡ ψ U ( ϕ ∧ ψ ) ∨ G ψ \phi R \psi \equiv \psi U (\phi \wedge \psi) \vee G \psi ϕRψ≡ψU(ϕ∧ψ)∨Gψ



























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










