图学习笔记（二）：图机器学习

回顾

图论的基本概念
图的表示和存储方式
同构图和异构图的分类
几个基础的图论算法

五. 图机器学习（GML：Graph Machine Learning）的发展

图机器学习（GML：Graph Machine Learning）

import numpy as np
import random
import networkx as nx
from IPython.display import Image
import matplotlib.pyplot as plt
from sklearn.metrics import accuracy_score
from sklearn.metrics import roc_curve
from sklearn.metrics import roc_auc_score

一. 图机器学习:图学习的主要任务(三种)

图学习中包含三种主要的任务：

• 链接预测（Link prediction）
• 节点标记预测（Node labeling）
• 图嵌入（Graph Embedding）

链接预测（Link prediction）

在链接预测中，给定图G，我们的目标是预测新边。例如，当图未被完全观察时，或者当新客户加入平台（例如，新的LinkedIn用户）时，预测未来关系或缺失边是很有用的。

新LinkedIn用户的链接预测只是给出它可能认识的人的建议。
在链路预测中，我们只是尝试在节点对之间建立相似性度量，并链接最相似的节点。现在的问题是识别和计算正确的相似性分数！

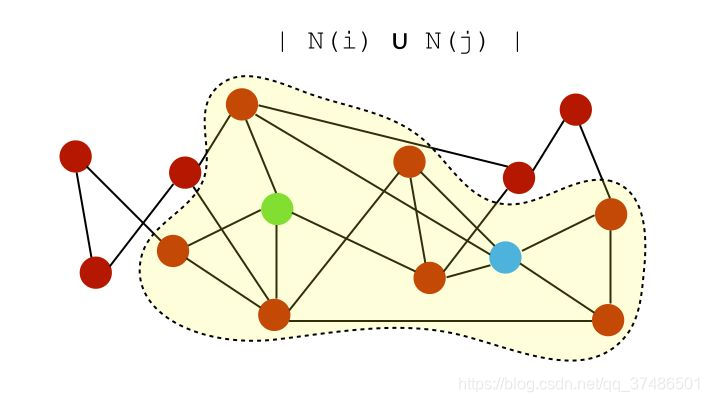
为了说明图中不同链路的相似性差异，让我们通过下面这个图来解释：

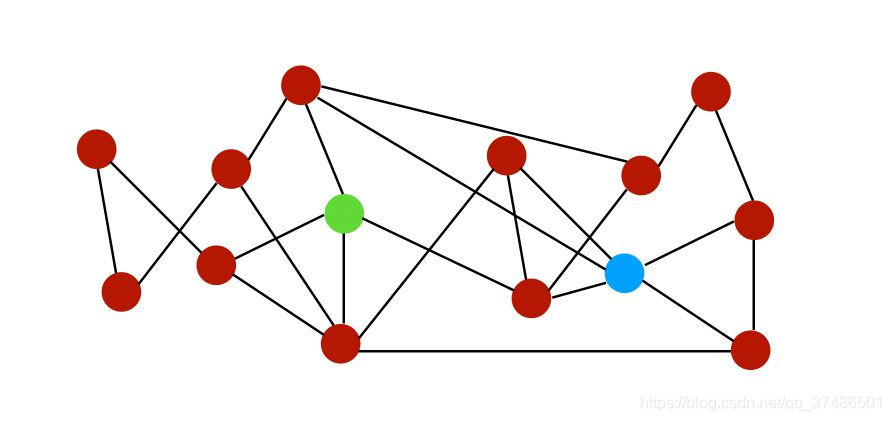
设N(i)是节点i的一组邻居。在上图中，节点i和j的邻居可以表示为：

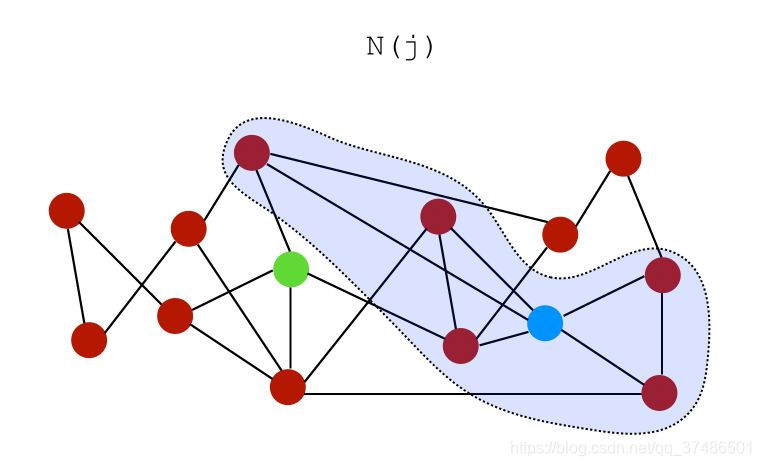
i的邻居：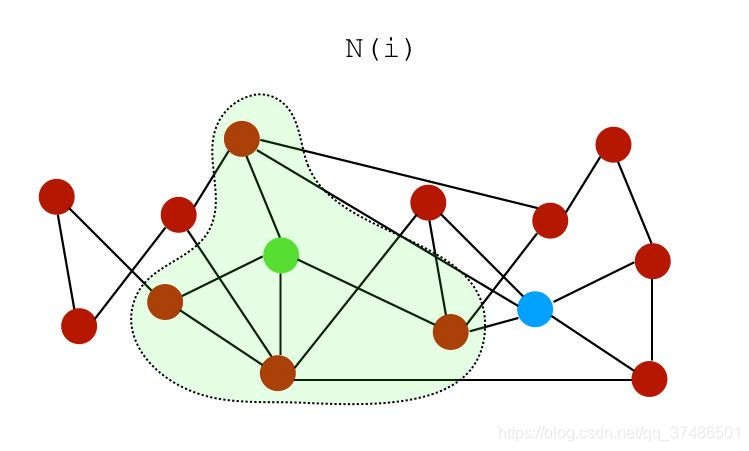

1. 相似度分数

我们可以根据它们的邻居为这两个节点建立几个相似度分数。

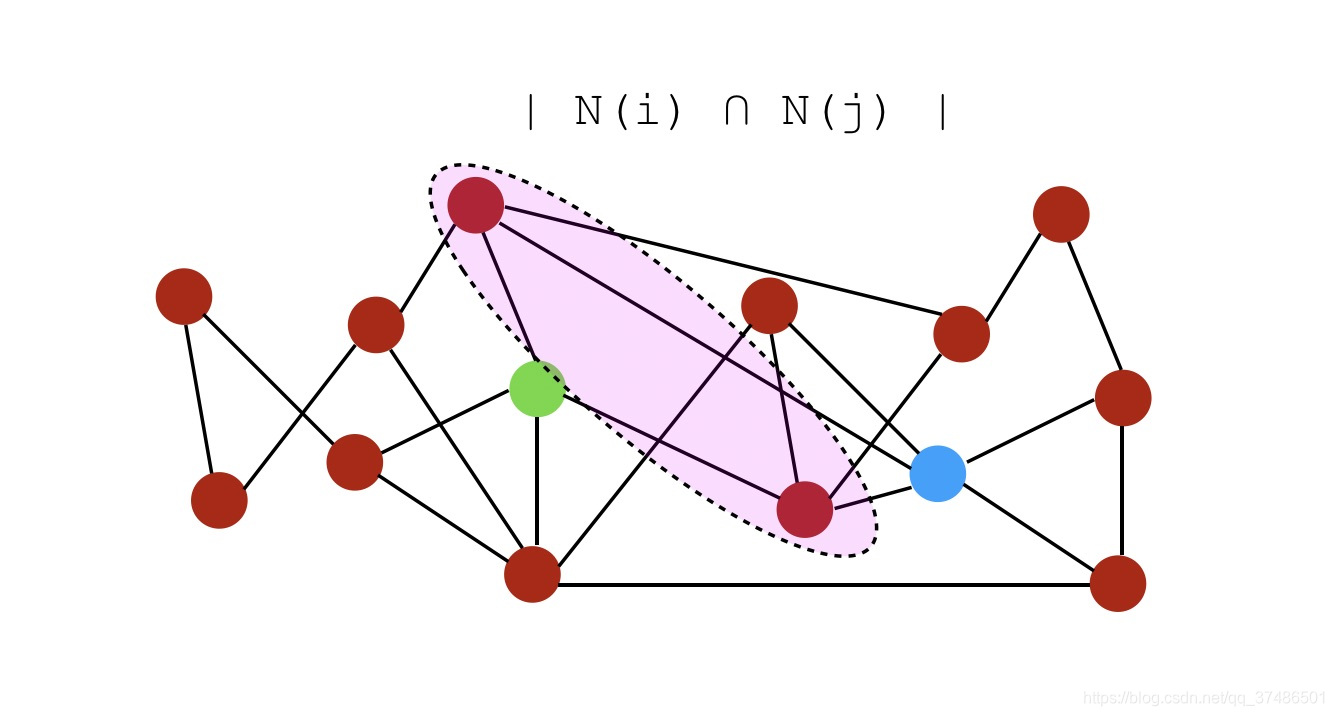
1.1 公共邻居

• 公共邻居：$S(i,j)=\mid N(i)\cap N(j)\mid$，即公共邻居的数量。在此示例中，分数将为2，因为它们仅共享2个公共邻居。
  

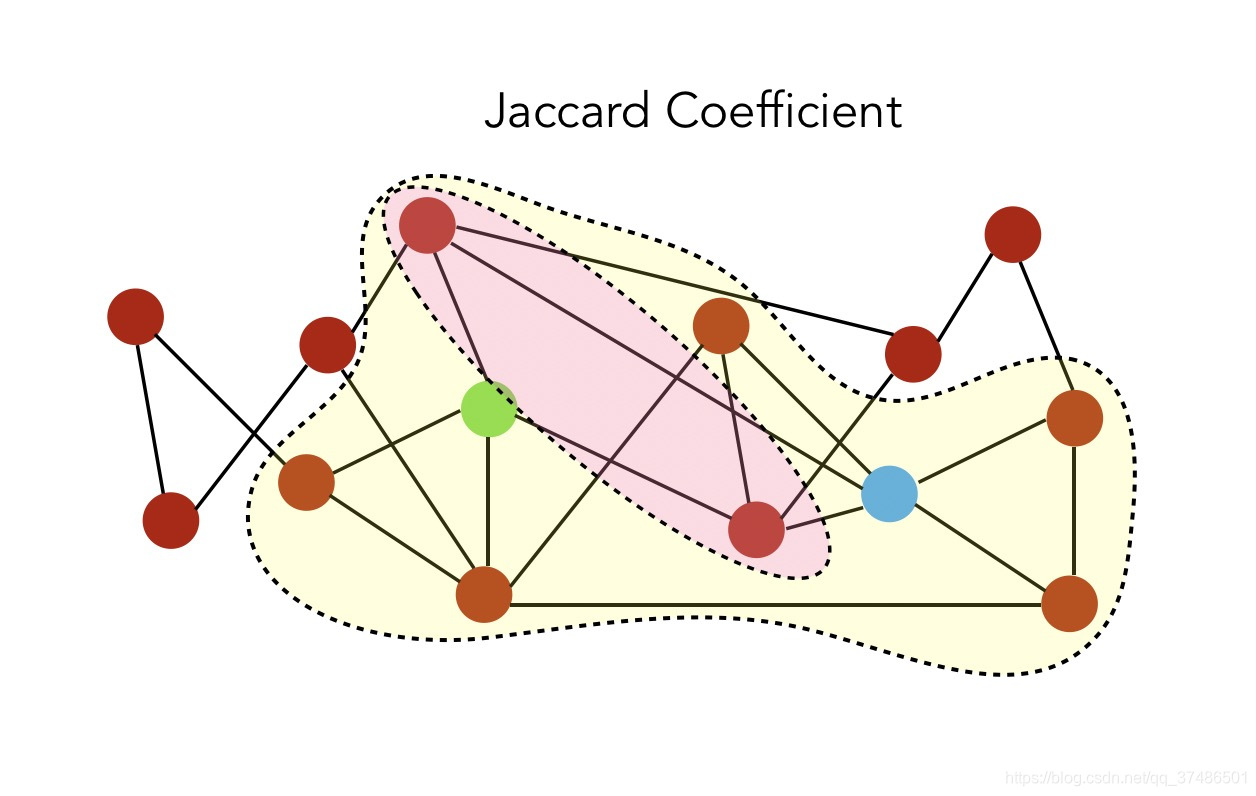
1.2 Jaccard系数

• Jaccard系数：$S(i,j)=\frac{\mid N(i)\cap N(j)\mid }{\mid N(i)\cup N(j)\mid }$​ ，标准化的共同邻居版本。
  交集是共同的邻居，并集是：
  
  因此，Jaccard系数由粉红色与黄色的比率计算出：值是$\frac{1}{6}$​。
  

1.3 Adamic-Adar指数

• Adamic-Adar指数：$S(i,j)={\sum }_{k\in N(i)\cap N(j)}\frac{1}{\log \mid N(k)\mid }$。 对于节点i和j的每个公共邻居（common neighbor），我们将1除以该节点的邻居总数。这个概念是，当预测两个节点之间的连接时，与少量节点之间共享的元素相比，具有非常大的邻域的公共元素不太重要。

1.4 优先依附

• 优先依附(Preferential attachment)： S(i,j)=∣N(i)∣∗∣N(j)∣S(i,j) = \mid N(i) \mid * \mid N(j) \midS(i,j)=∣N(i)∣∗∣N(j)∣
• 当社区信息可用时，我们也可以在社区信息中使用它们。

2. 性能指标(Performance metrics)

我们如何进行链接预测的评估？我们必须隐藏节点对的子集，并根据上面定义的规则预测它们的链接。这相当于监督学习中的train/test的划分。 然后，我们评估密集图的正确预测的比例，或者使用稀疏图的标准曲线下的面积(AUC)。
关于更多性能评价介绍，可以阅读博客模型评估指标AUC和ROC
https://blog.csdn.net/liweibin1994/article/details/79462554

这里继续用空手道俱乐部图来举例：

import numpy as np
import random
import networkx as nx
from IPython.display import Image
import matplotlib.pyplot as plt
from sklearn.metrics import accuracy_score
from sklearn.metrics import roc_curve
from sklearn.metrics import roc_auc_score



# 我们导入空手道俱乐部图
n=34
m = 78
G_karate = nx.karate_club_graph()

pos = nx.spring_layout(G_karate)
nx.draw(G_karate, cmap = plt.get_cmap('rainbow'), with_labels=True, pos=pos)


# 我们首先把有关图的信息打印出来：
n = G_karate.number_of_nodes()
m = G_karate.number_of_edges()
print("Number of nodes : %d" % n)
print("Number of edges : %d" % m)
print("Number of connected components : %d" % nx.number_connected_components(G_karate))

plt.figure(figsize=(12,8))
nx.draw(G_karate, pos=pos)
plt.gca().collections[0].set_edgecolor("#000000")

# 现在，让我们删除一些连接，例如25％的边：
# Take a random sample of edges
edge_subset = random.sample(G_karate.edges(), int(0.25 * G_karate.number_of_edges()))
# remove some edges
G_karate_train = G_karate.copy()
G_karate_train.remove_edges_from(edge_subset)


# 绘制部分观察到的图，可以对比上图发现，去掉了一些边
plt.figure(figsize=(12,8))
nx.draw(G_karate_train, pos=pos)




# 你可以打印我们删除的边数和剩余边数：
edge_subset_size = len(list(edge_subset))
print("Deleted : ", str(edge_subset_size))
print("Remaining : ", str((m - edge_subset_size)))



计算Jaccard Coefficient
# 我们可以先使用Jaccard系数进行预测：
# Make prediction using Jaccard Coefficient
pred_jaccard = list(nx.jaccard_coefficient(G_karate_train))
score_jaccard, label_jaccard = zip(*[(s, (u,v) in edge_subset) for (u,v,s) in pred_jaccard])
# 打印前10组结果
print(pred_jaccard[0:10])
# 预测结果如下，其中第一个是节点，第二个是节点，最后一个是Jaccard分数（用来表示两个节点之间边预测的概率）

# 然后我们可以使用ROC-AUC标准来比较不同模型的性能，因为我们既有真实的边（label），也有预测边的概率（score）
# Compute the ROC AUC Score
# 其中，FPR是False Positive Rate， TPR是True Positive Rate
fpr_jaccard, tpr_jaccard, _ = roc_curve(label_jaccard, score_jaccard)
auc_jaccard = roc_auc_score(label_jaccard, score_jaccard)
print(auc_jaccard)



计算Adamic-Adar
# 我们现在计算Adamic-Adar指数和对应的ROC-AUC分数
# Prediction using Adamic Adar 
pred_adamic = list(nx.adamic_adar_index(G_karate_train))
score_adamic, label_adamic = zip(*[(s, (u,v) in edge_subset) for (u,v,s) in pred_adamic])
print(pred_adamic[0:10])
# Compute the ROC AUC Score
fpr_adamic, tpr_adamic, _ = roc_curve(label_adamic, score_adamic)
auc_adamic = roc_auc_score(label_adamic, score_adamic)
print(auc_adamic)


计算Preferential Attachment
# 同样，我们可以计算Preferential Attachment得分和对应的ROC-AUC分数
# Compute the Preferential Attachment
pred_pref = list(nx.preferential_attachment(G_karate_train))
score_pref, label_pref = zip(*[(s, (u,v) in edge_subset) for (u,v,s) in pred_pref])
print(pred_pref[0:10])
fpr_pref, tpr_pref, _ = roc_curve(label_pref, score_pref)
auc_pref = roc_auc_score(label_pref, score_pref)
print(auc_pref)


绘制ROC-AUC来评价预测的效果
plt.figure(figsize=(12, 8))
plt.plot(fpr_jaccard, tpr_jaccard, label='Jaccard Coefficient - AUC %.2f' % auc_jaccard, linewidth=4)
plt.plot(fpr_adamic, tpr_adamic, label='Adamic-Adar - AUC %.2f' % auc_adamic, linewidth=4)
plt.plot(fpr_pref, tpr_pref, label='Preferential Attachment - AUC %.2f' % auc_pref, linewidth=4)
plt.plot([0, 1], [0, 1], 'k--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.0])
plt.xlabel('False positive rate')
plt.ylabel('True positive rate')
plt.title("ROC AUC Curve")
plt.legend(loc='lower right')
plt.show() 

节点标记预测（Node labeling）

节点标记预测（Node labeling）：给定一个未标记某些节点的图，我们希望对这些节点的标签进行预测。这在某种意义上是一种半监督的学习问题。

处理这些问题的一种常见方法是假设图上有一定的平滑度。平滑度假设指出通过数据上的高密度区域的路径连接的点可能具有相似的标签。这是标签传播算法背后的主要假设。

标签传播算法（Label Propagation Algorithm,LPA）是一种快速算法，仅使用网络结构作为指导来发现图中的社区，而无需任何预定义的目标函数或关于社区的先验信息。

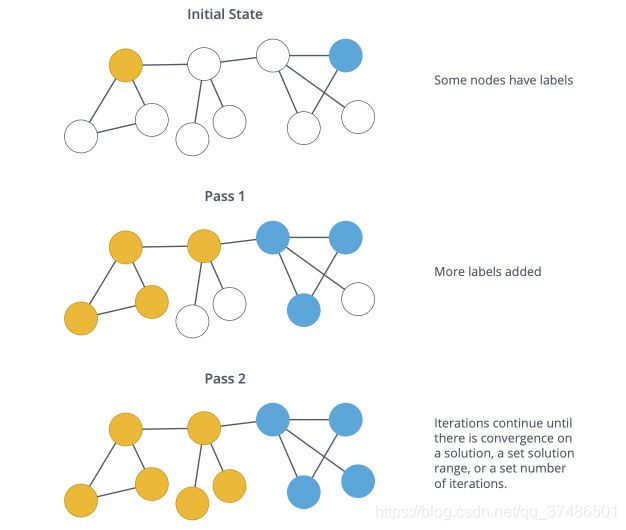
单个标签在密集连接的节点组中迅速占据主导地位，但是在穿过稀疏连接区域时会遇到问题。

半监督标签传播算法是如何工作？首先，我们有一些数据$x_1,...,x_l,x_{l+1},...,x_n\in R^p$，以及前$l$个点的标签：$y_1,...,y_l\in 1...C$

我们定义初始标签矩阵$Y\in R^{n\times C}$，如果$x_i$具有标签$y_i=j$则$Y_{ij}=1$，否则为0。该算法将生成预测矩阵$F\in R^{n\times C}$，我们将在下面详述。然后，我们通过查找最可能的标签来预测节点的标签：
$Yi{}^{}=argmaxjFi,j$
预测矩阵$F$是什么？

预测矩阵是矩阵$F^{\star }$，其最小化平滑度和准确度。因此，我们的结果在平滑性和准确性之间进行权衡。
问题的描述非常复杂，所以我将不会详细介绍。但是，解决方案是：
$F\star =((1-\alpha )I+Lsym{)}^{-1}Y$
其中：
参数$\alpha =\frac{1}{1+\mu }$
$Y$是给定的标签
$L_{sym}$是图的归一化拉普拉斯矩阵（Laplacian matrix）

如果您想进一步了解这个主题，请关注图函数的平滑度和流形正则化的概念。

图嵌入（Graph Embedding）

在处理NLP或计算机视觉问题时，我们习惯在深度神经网络中对图像或文本进行嵌入(embedding)。到目前为止，我们所看到的图的一个局限性是没有向量特征。但是，我们可以学习图的嵌入！图有不同几个级别的嵌入：

• 对图的组件进行嵌入（节点，边，特征…）(Node2Vec)
• 对图的子图或整个图进行嵌入==(Graph2Vec)==

小结

图的介绍，图的主要类型，不同的图算法，在Python中使用Networkx来实现它们，以及用于节点标记，链接预测和图嵌入的图学习技术。

毋庸置疑，这只是冰山一角。图论不断扩展，我认为列出一些资源以进一步学习是有用的：
图卷积网络(Graph Convolution Networks): https://towardsdatascience.com/how-to-do-deep-learning-on-graphs-with-graph-convolutional-networks-7d2250723780
图和流形上的几何深度学习(Geometric Deep Learning on Graphs and Manifolds):http://www.geometricdeeplearning.com/
一个可以提供帮助的MOOC:https://www.edx.org/course/advanced-algorithmics-and-graph-theory-with-python
斯坦福图学习入门课程cs224w——图网络机器学习算法：http://cs224w.stanford.edu/
cs224w课程视频可在https://www.bilibili.com/video/av30039828

参考材料：
https://blog.csdn.net/xjxgyc/article/details/100175930
https://maelfabien.github.io/
https://maelfabien.github.io/machinelearning/graph_4/
https://maelfabien.github.io/machinelearning/graph_5/
A Comprehensive Guide to Graph Algorithms in Neo4j, Mark Needham & Amy E. Hodler
Networkx documentation, https://networkx.github.io/documentation/stable/
Graph Theory courses at Telecom Paris
Learning in Graphs with Python (Part 3)