算法竞赛进阶指南读书笔记——0x11栈

栈

定义：“先进后出”的线性数据结构，只能在栈顶添加或删除元素

性质：

1. 只能在栈顶添加或删除元素，支持$O(1)$入栈、出栈
2. 有且只有一个栈顶

存储：

数组模拟+变量记录栈顶位置，如图：

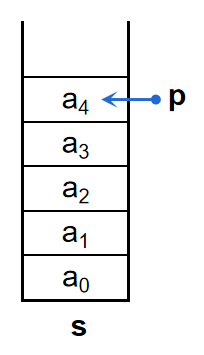
操作：

1. 建栈$initialize()$:

   新建数组，令$p=-1$（此时栈顶无元素）

2. 入栈$push(x)$:

   更新栈顶，将$x$放入新栈顶处

3. 栈顶$top()$:

   返回栈顶元素$s[p]$

4. 出栈$pop()$:

   （返回栈顶元素，）更新栈顶

实现：

int s[N], p = -1; // initialize

s[++p] = x; // push

x = s[p]; // top

x = s[p--]; // pop

例1 $O(1)$查询栈最小值。

思路：

由于栈顶只有一个，栈的最小值也只有一个，我们考虑用另一个栈来维护原栈($s_0$)当前的最小值，且该最小值位于新栈($s_1$)的栈顶。

元素$x$入栈$s_0$时，将$\min (top(s_1),x)$压入栈$s_1$，若$x⩾top(s_1)=\min (s_0)$，则$x$对$s_0$最小值无影响；若$x<top(x_1)=\min (s_0)$，则实现对$s_0$最小值的更新。由于在每一时刻$s_1.top()$都是$\min (s_0)$，故$s_1[n]=\underset{1⩽i⩽n}{\min }{s}_0[i]$.

元素$x$出栈时，直接同步对$s_1$执行$pop()$即可，新栈顶将是出栈前$s_0$子栈的最小值——即当前出栈后的$s_0$的最小值。

实现：

void push(int x) { s0[++p0] = x, s1[++p1] = min(s1[p1], x); }

void pop(int x) { p0--, p1--; }

int getMin() { return s1[p1]; }

例2 Editor

思路：对顶栈

当我们需要维护区间中位置相对固定的点时，可以采用“对顶”的思想。比如动态维护中位数时，我们同样利用了“对顶”的思想，结合堆维护有序数据的性质，设计出对顶堆的算法。

同样地，由于后输入的文字在退格时先被删除，符合栈“后进先出”的性质，我们可以采用对顶栈来实现这样的编辑器，并将对顶的位置设在光标（前的一个字符）$p$处，让栈$A$维护$[0,p]$的序列，栈$B$维护$[p+1,n]$的序列，如图：

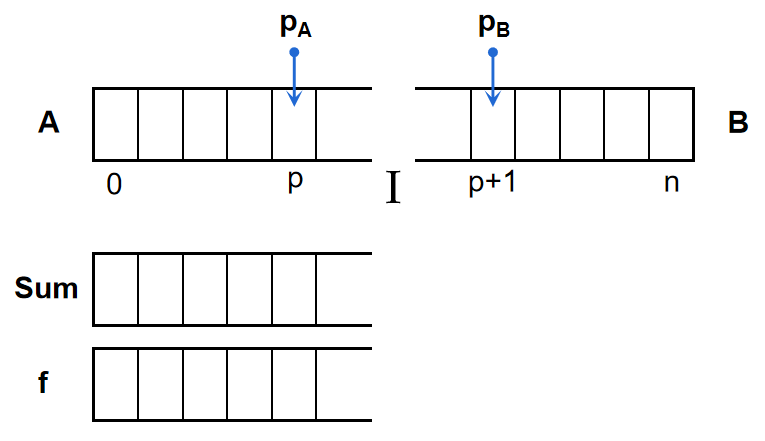
当我们向栈$A$中加数时，同时维护它的前缀和（共用$p_A$，结构类似栈），并利用例1的思路维护前缀和的最大值。

对于5种操作，步骤如下：

• $Ix$：$A.push(x)$，更新前缀和，维护前缀和的最大值
• $D$：$A.pop()$（原先的前缀和自然覆盖）
• $L$：$B.push(A.pop())$
• $R$：$A.push(B.pop())$，此时向$A$中加数，需同步更新前缀和与前缀和的最大值
• $Qk$：同例1，$f[k]$

实现：

pa = pb = 0, f[0] = -INF; // 涉及求前缀和,栈从下标1开始存; 前缀和可能为负,初始化为负无穷
cin >> q;
while (q--) {
  cin >> op;
  switch (op) {
  case 'I':
    cin >> x;
    a[++pa] = x;
    s[pa] = s[pa - 1] + a[pa];
    f[pa] = max(f[pa - 1], s[pa]);
    break;
  case 'D':
    if (pa)
      pa--;
    break;
  case 'L':
    if (pa)
      b[++pb] = a[pa--];
    break;
  case 'R':
    if (pb) {
      a[++pa] = b[pb--];
      s[pa] = s[pa - 1] + a[pa];
      f[pa] = max(f[pa - 1], s[pa]);
    }
    break;
  case 'Q':
    cin >> x;
    cout << f[x] << endl;
    break;
  }
}

例3 进出栈序列问题

思路1：暴搜

边界是栈空或所有元素均已入栈，有两种选择：

1. 将下一个数入栈
2. 出栈

时间复杂度$O(2^n)$.

实现：

void dfs(int dep, int in) { // 操作次数, 已入栈的数的个数
  if (cnt == 20)
    return;
  if (dep == n << 1) {
    for (int i = 0; i < n; i++)
      cout << a[i];
    cout << endl;
    cnt++;
    return;
  }
  if (p) {
    a[dep - in] = s[p--];
    dfs(dep + 1, in);
    s[++p] = a[dep - in]; // 回溯,入栈
  }
  if (in < n) {
    s[++p] = in + 1;
    dfs(dep + 1, in + 1);
    p--; // 回溯,出栈
  }
}

dfs(0, 0);

思路2：递推+高精

设$n$个元素$(1,\cdots ,n)$按序进栈方案数为$S_n$.考虑出栈序列中的1，最终将排在$k$号位$(1⩽k⩽n)$，共有$n$种情况。

对于每一种情况，都是前$k-1$个元素先入栈出栈，然后1入栈出栈，接着剩余的$n-k$个元素入栈出栈。由于$S_n$仅与$n$有关，而与序列中具体元素无关，故由乘法原理得
$$S_n=\sum _{k=1}^n{S}_{k-1}{S}_{n-k}$$
实际递推时，边界$S_0=1$，从$S_1$开始逐步算至$S_n$；计算$S_n$时，需保证$S_1,\cdots ,S_{n-1}$已经计算好。

复杂度$O(n^2)$，显然6e4过不了$n^2$，加之高精常数巨大，交付OJ过不了500，本地O2能过700.

实现：

高精：

struct number {
  int len;
  vector<int> n;
  number &operator=(const char *);
  number &operator=(int);
  number();
  number(int);
  number operator*(const number &) const;
  number operator+(const number &) const;
  number &operator+=(const number &);
} s[N];

number &number::operator=(const char *c) {
  n.clear();
  len = 1;
  int l = strlen(c), k = 1, tmp = 0;
  for (int i = 1; i <= l; i++) {
    if (k == 10000) {
      n.push_back(tmp);
      len++, k = 1, tmp = 0;
    }
    tmp += k * (c[l - i] - '0');
    k *= 10;
  }
  n.push_back(tmp);
  return *this;
}

number &number::operator=(int a) {
  char s[15];
  sprintf(s, "%d", a);
  return *this = s;
}

number::number() {
  n.clear();
  n.push_back(0);
  len = 1;
}

number::number(int n) { *this = n; }

number number::operator+(const number &b) const {
  if (len > b.len)
    return b + *this;
  number c;
  c.len = b.len;
  for (int i = 0; i < c.len; i++)
    c.n.push_back(0);
  c.n.push_back(0);
  for (int i = 0; i < c.len; i++) {
    if (i >= len)
      c.n[i] += b.n[i];
    else
      c.n[i] += n[i] + b.n[i];
    if (c.n[i] >= 10000) {
      c.n[i] -= 10000;
      c.n[i + 1]++;
    }
  }
  if (c.n[c.len])
    c.len++;
  else
    c.n.pop_back();
  return c;
}

number number::operator*(const number &b) const {
  number c;
  c.len = len + b.len + 1;
  for (int i = 0; i < c.len; i++)
    c.n.push_back(0);
  for (int i = 0; i < len; i++)
    for (int j = 0; j < b.len; j++) {
      c.n[i + j] += n[i] * b.n[j];
      c.n[i + j + 1] += c.n[i + j] / 10000;
      c.n[i + j] %= 10000;
    }
  while (c.n[c.len - 1] == 0 && c.len > 1) {
    c.len--;
    c.n.pop_back();
  }
  return c;
}

number &number::operator+=(const number &b) { return *this = *this + b; }

ostream &operator<<(ostream &o, number &a) {
  o << a.n[a.len - 1];
  for (int i = a.len - 2; i >= 0; i--) {
    o.width(4);
    o.fill('0');
    o << a.n[i];
  }
  return o;
}

算法主体：

s[0] = 1;
for (int i = 1; i <= n; i++)
  for (int j = 1; j <= i; j++)
    s[i] += s[j - 1] * s[i - j];
cout << s[n] << endl;

思路3：DP

当一个元素已经出栈后，我们无法通过任何操作来改变它的位置了，它对答案已没有贡献。所以我们能把握的只能是当前仍未入栈的元素以及栈中的元素，调整它们的顺序可以给答案带来贡献。

设状态$f_{i,j}\triangleq i$个数未入栈，$j$个数在栈中的方案总数，我们要么出栈、要么入栈，转移方程为

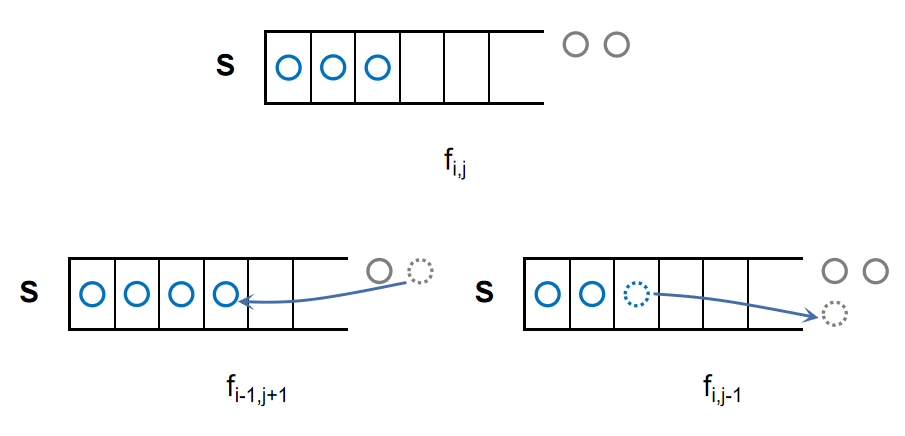
$$f_{i,j}=f_{i-1,j+1}+f_{i,j-1}(j⩾1)$$
边界$f_{0,0}=1$，即$n=0$的情形；$f_{i,0}=f_{i-1,1}$，无法再出栈；$f_{0,j}=f_{0,j-1}$，无法再入栈。最终答案为$f_{n,0}$.

由于等号右边$i-1$小于等号左边的$i$，我们先$i$后$j$进行转移；由于最终要求$f_{n,0}$，只需转移到$f_{i,n-i}$即可。

时空复杂度均$O(n^2)$，由于不涉及高精度乘法，常数小于上一种解法，OJ能跑过500，本地O2能过1500，但空间复杂度奇高，开6e5*6e5会CE，1e3*1e3会MLE.

实现（高精同上）：

for (int i = 0; i <= n; i++)
  f[0][i] = 1;
for (int i = 1; i <= n; i++)
  for (int j = 0; j <= n - i; j++)
    f[i][j] = j ? f[i - 1][j + 1] + f[i][j - 1] : f[i - 1][j + 1];
cout << f[n][0] << endl;

思路4：数学

将入栈视作0，出栈视作1，问题转化为求前缀0多于前缀1的0-1串个数。结合组合数学知识知，即求第$n$项卡特兰数
$$Ca{t}_n=\frac{C_{2n}^n}{n+1}$$
实现1：暴力计算

我们将组合数代入，原始进一步化简为
$$Ca{t}_n=\frac{\prod _{i=n+2}^{2n}i}{n!}$$
分别算出分子分母，再做除法。由于高精乘未采用FFT优化，复杂度爆炸，交付OJ大概能过5000.

高精度除法（二分优化）：

number number::operator/(const number &b) const {
  number c, tmp;
  c.len = len;
  for (int i = 0; i < c.len; i++)
    c.n.push_back(0);
  for (int i = len - 1; i >= 0; i--) {
    tmp = tmp * 10000 + n[i];
    int l = 0, r = 9999, mid;
    while (l < r) {
      mid = (l + r) >> 1;
      if (b * (number)mid <= tmp)
        l = mid + 1;
      else
        r = mid;
    }
    c.n[i] = --l;
    tmp -= b * (number)l;
  }
  while (c.n[c.len - 1] == 0 && c.len > 1) {
    c.len--;
    c.n.pop_back();
  }
  return c;
}

number &number::operator/=(const number &b) { return *this = *this / b; }

依赖（高精乘同上）：

bool number::operator>(const number &b) const {
  if (len != b.len)
    return len > b.len;
  for (int i = len - 1; i >= 0; i--)
    if (n[i] != b.n[i])
      return n[i] > b.n[i];
  return false;
}

bool number::operator<=(const number &b) const { return !(*this > b); }

number number::operator-(const number &b) const {
  number c;
  c.len = len;
  for (int i = 0; i < len; i++)
    c.n.push_back(0);
  for (int i = 0; i < len; i++) {
    c.n[i] += n[i] - b.n[i];
    if (c.n[i] < 0) {
      c.n[i] += 10000;
      c.n[i + 1]--;
    }
  }
  while (c.n[c.len - 1] == 0 && c.len > 1) {
    c.len--;
    c.n.pop_back();
  }
  return c;
}

number &number::operator-=(const number &b) { return *this = *this - b; }

算法主体：

number a = 1, b = 1;
int n;
cin >> n;
for (int i = 2; i <= n; i++) a *= i;
for (int i = n + 2; i <= n << 1; i++) b *= i;
b /= a;
cout << b << endl;

实现2：质因数分解

在上一个实现中，我们减少计算次数的主要思路是对分子分母进行约分，但由于约分不彻底导致我们进行了数次“无效计算”。事实上，最终答案应该是一个整数，从质因数分解的角度来说，如果我们能把最终的答案化成$\prod p_i^{c_i}$的形式，配合快速幂，我们将极大的减少重复的无效计算，同时也能避免编写繁琐的高精度除法。

为此，我们将分子分母同时进行质因数分解，即
$$Ca{t}_n=\frac{(2n)!}{n!(n+1)!}=\frac{(2n)!}{(n+1)(n!{)}^2}=\frac{\prod p_{1i}^{c_{1}i}}{\prod p_{2i}^{c_{2}i}(\prod p_{3i}^{c_{3}i}{)}^2}$$

在质因数分解之前，我们需要先筛素数，然后再利用Legendre公式($v_p(n!)=\sum _{k=1}^{+\infty }\lfloor \frac{n}{p^k}\rfloor$)求出阶乘的质因数分解。对于$n+1$的处理，我们直接对它进行多次除法到除不尽即可。

但由于本题过于毒瘤，我们还需对高精的常数进行优化。由于$n⩽6e4$，所有的质数都落在int范围内，所以我们可以把高精乘写作高精乘低精版本将其复杂度降到稳定$O(n)$；由于输出量偏大，我们采用putchar进行快输。

高精（优化）：

inline number number::operator*(const int &b) const {
  long long tmp = 0, cur;
  number c;
  c.len = len;
  for (int i = 1; i < c.len; i++) // 1.
    c.n.push_back(0);
  for (int i = 0; i < len; i++) {
    cur = n[i] * b + tmp;
    tmp = cur / 10000, c.n[i] = cur % 10000;
  }
  while (tmp) {
    c.n.push_back(tmp % 10000);
    c.len++, tmp /= 10000;
  }
  return c;
}

inline void print(int x, int i = 4) { // 借递归形式保持固定输出位数
  if (!i)
    return;
  print(x / 10, i - 1);
  putchar(x % 10 ^ 48);
}

细节：

1. 事实上，笔者在之前的高精板子中无意留下了这个瑕疵。由于初始时c.len为1，所以不需要从0开始循环；但由于之前的板子在末尾进行了删0操作，保证了正确性，而此处并没有类似操作而导致错误。麻烦读者自行更正。

算法主体：

inline int qpow(int a, int b) { // 1.
  int res = 1;
  for (; b; b >>= 1) {
    if (b & 1)
      res *= a;
    a *= a;
  }
  return res;
}

int main() {
  int n;
  number ans = 1;
  scanf("%d", &n);
  for (int i = 2; i <= n << 1; i++) {
    if (!nt_prime[i]) {
      p[++cnt] = i;
      for (int j = (n << 1) / i; j; j /= i) // 分解(2n)!
        c[cnt] += j;
      for (int j = n / i; j; j /= i) // 分解(n!)^2
        c[cnt] -= j << 1;
      for (int j = n + 1; !(j % i); j /= i) // 分解n+1
        c[cnt]--;
    }
    for (int j = 1; p[j] <= (n << 1) / i; j++) { // 线性筛素数
      nt_prime[p[j] * i] = true;
      if (!(i % p[j]))
        break;
    }
  }
  for (int i = 1; i <= cnt; i++)
    if (c[i])
      ans *= qpow(p[i], c[i]); // 快速幂累计答案
  printf("%d", ans.n[ans.len - 1]); // 最高位直接输出
  for (int i = ans.len - 2; i >= 0; i--)
    print(ans.n[i]);
  return 0;
}

细节：

1. 事实证明，因子幂次不会太高，int足够使用
2. 由于基于vector的压位高精常数偏大，仍需加入pragma指令注入氧气或臭氧

表达式计算

分类

表达式类型	定义
中缀表达式	A op B
前缀表达式	op A B
后缀表达式	A B op

后缀表达式求值

根据后缀表达式的定义，我们可以将一个后缀表达式做如下划分：

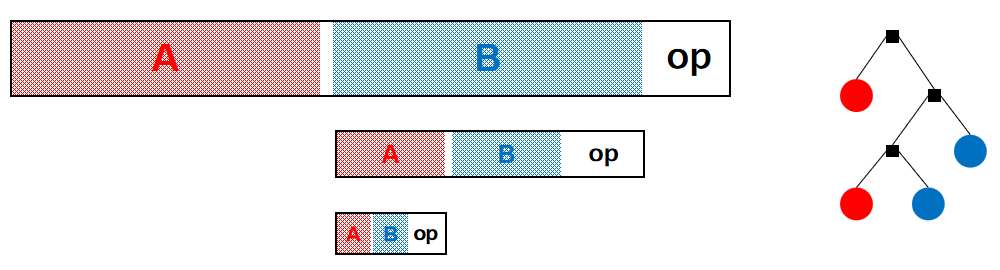我们可以将计算后缀表达式的基本单位$ABop$看作一个函数$f(a,b,op)$，并将嵌套的计算看作一种递归的形式，例如将上图看作$f(a,f(f(a,b,op),b,op),op)$.

接着，我们用栈来模拟递归的实现。

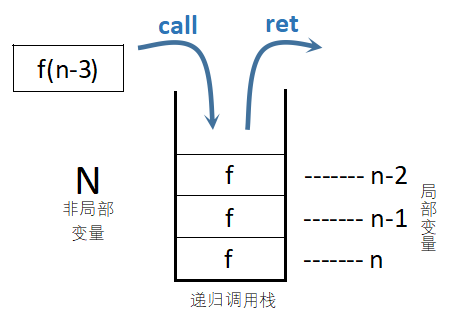
当读到$A$时，我们进入该层的函数调用；而读到操作符后我们完成计算，执行返回。按照先后顺序，我们依次将后缀表达式的操作数入栈，以模拟函数的层层调用操作；当我们读到操作符后，我们取出当前位于栈顶的两个变量（即当前调用函数作用域中的变量）完成计算，将其出栈实现返回，接着将结果再次以操作数的身份入栈，即$f(a,f(a,b,op),op)$中的$f(a,b,op)$的值作为参数传入外层函数调用中。

步骤：

1. 逐一扫描表达式中的元素
2. 如果遇到数字，将数字入栈
3. 如果遇到运算符，将栈顶两个数出栈并计算，将计算结果入栈
4. 最后栈中所剩的一个数即答案（最外层调用返回）

中缀表达式转后缀表达式

由于乘除与加减的运算优先级不同，为了简化考虑，我们将所有乘除的运算优先级与同级运算符从左到右的计算顺序用括号进行表达。例如对于表达式$(3+4)\ast 2-1$，我们添加括号使之成为$((3+4)\ast 2)-1$，以突出$2$与$(3+4)$结合的优先级。

在添完括号后，我们便将各种运算符一视同仁，只考虑操作符$op$与括号。

回顾中缀表达式与后缀表达式的定义，中缀表达式为$AopB$，后缀表达式为$ABop$，可见各操作数的相对位置并没有发生改变，我们只需要决定$op$所在的位置即可。

按照上文的思路，我们依旧将表达式计算看作递归调用的形式。以表达式$((3\circ 4)\circ 2)\circ (1\circ 5)$为例，递归形式可以写作$f(f(f(3,4,op),2,op),f(1,5,op),op)$.

与上文类似的，由于数字的相对位置并没有发生改变，我们只需要判断函数何时应执行返回，并将操作符放置在调用的末尾位置，这样后缀表达式才能通过符号来正确的意识到递归调用的终点所在。观察表达式本身，我们不难发现，递归调用的结束标志为’)'。

在一次递归调用结束之前，我们不能将符号直接给出，而且在后续调用的函数还未返回时，也不能给出该符号，只用当两个操作数都完整给出后，我们才可以输出对应的运算符。这与递归调用（或栈）的行为一致。而左括号标记了该层调用的起点，同样需要入栈，以将该调用完整的返回；否则，当遇到右括号执行出栈操作时，并不知道该层调用的边界在哪里，便无从决定出栈的符号应有多少个。

这样，对于完整添加括号的表达式，我们可以按照这样的流程来进行转换：(1)逐一扫描表达式的元素，如果碰到数字，直接输出 (2)若碰到’(‘，将其入栈 (3)若碰到’)‘，不断执行出栈操作直到当前栈顶为’(‘，并将’('出栈 (4)如果碰到运算符，直接入栈 (5)最后将所有符号出栈（最外层调用返回，即将表达式理解为$(((3\circ 4)\circ 2)\circ (1\circ 5))$的形式）

而事实情况并非如此，原始表达式通过运算顺序与优先级减少括号数。先解决同级运算符的问题。表达式$(1+2)+3$与$1+2+3$的区别在于没有右括号来帮助1,2之间的加号出栈。这时候，由于运算的优先级相同，后进来的运算符需要帮助位于同层调用的运算符出栈。如此例中，第二个‘+’进栈前，需要将当前栈中所有的符号（恰位于同级）出栈，接着再将其入栈，以实现$1\circ 2\circ \cdots \circ n\to (((1\circ 2)\circ 3)\circ \cdots )\circ n$的效果。

落实到实现中，我们只需要对(4)进行修正：如果碰到运算符，先执行出栈操作，直到栈顶为’(‘（’(‘不出栈，凡’(‘必有帮助其出栈的’)'（相匹配的括号），无需运算符帮助（步骤(3)）），接着将新操作符入栈。

再解决运算优先级的问题。通过对比表达式$((3+4)\ast 2)-1$与$(3+4)\ast 2-1$可以看出，在出现了高优先级运算符与低优先级运算符与同一个数字进行连接时，我们需要右括号来帮助高优先级运算符出栈，即$\bullet a)\circ$（其中$\bullet >\circ$）的基本结构。

因此，低优先级的加减符号除了需要帮助同优先级的运算符出栈，还需承担此处右括号的工作，帮助高优先级的运算符出栈，以实现$\bullet a\circ \to \bullet a)\circ$的效果。

对(4)进行进一步的修正，我们得到转换步骤如下：

1. 逐一扫描表达式的元素，如果碰到数字，直接输出
2. 若碰到’('，将其入栈
3. 若碰到’)‘，不断执行出栈操作直到当前栈顶为’(‘，并将’('出栈
4. 如果碰到运算符，若栈顶运算符优先级不低于自身，则不断执行出栈操作，最后将该符号入栈（优先级：$\ast />+-$）
5. 最后将所有符号出栈（最外层调用返回）

中缀表达式递归求值

设$f(l,r)$对表达式$S[l,r]$进行求值，我们来考虑其与子问题的关系。

原问题$S[l,r]$有这样几种形式：

1. $()\circ \cdots \circ ()$（有不被括号包裹的运算符）：此时我们只需要选定一个括号外符号（不妨设选最后一个），分成两半递归求解，再利用$op$运算两部分来合并子问题即可
2. $(\cdots )$（没有不被括号包裹的运算符，且首尾是括号）：此时我们应执行去括号操作，递归求解$f(l+1,r-1)$
3. $\cdots$（没有运算符）：直接返回该数字即可

这样便可以在$O(n^2)$的时间完成中缀表达式的递归求值。

单调栈

例4 Largest Rectangle in a Histogram

思路：单调栈

顾名思义，单调栈中的元素具有一定的单调性，此题中，我们用单调栈来维护这些矩形的高，使得从栈底到栈顶存放的矩形高度依次递增。

维护单调性（不妨设单调递增）的意义在于，矮矩形无法容纳高矩形的延伸，而高矩形总可以容纳矮矩形的延伸，且最长的延伸为对应高度的最优解。又由于矩形高度具有单调性，我们只需考虑向后延伸即可，如图：

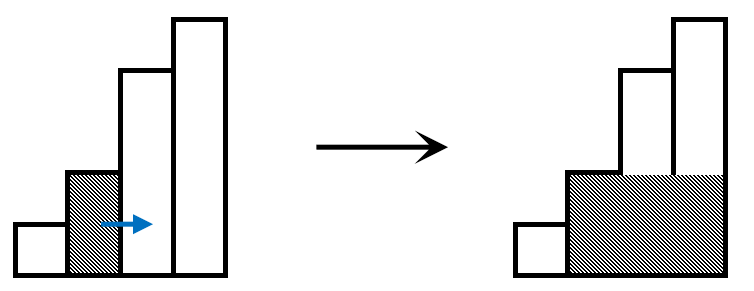
按照这样的想法，我们依次考虑每一个高度，若当前高度高于栈顶高度，我们将它的最大宽度初始化为1，并将它入栈。初始化宽度为1的因为它是当前最右侧的矩形，并没有可以延伸的空间，故对应的宽度仅仅是它自身的宽度而已；并且我们并没有对已经在栈中的矩形进行宽度的更新，因为根据上图的想法，我们仍然在持续延伸矩形的宽度，当前还并没有得到最终的宽度，并不急着更新。

而如果当前的高度低于栈顶的高度，部分矩形将无法继续延伸，我们进入宽度统计与答案统计的环节，如图：

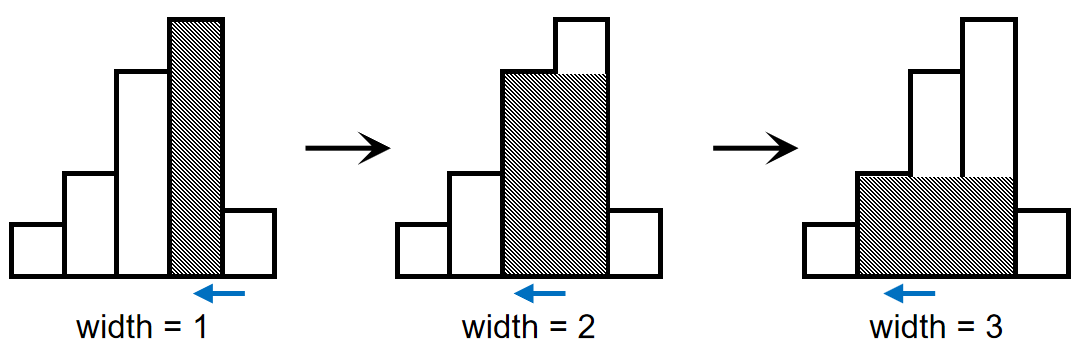
由于矩形高度满足单调性，后一个矩形总能容纳前一个矩形的延伸，所以我们依次累加每个矩形的宽度，即可在出栈的同时计算出该高度对应的最大宽度。同时，由于我们已经拿到了该高度的最大宽度，这个高度的矩形的计算已经完成，我们直接利用得到的宽度来更新答案。

由于单调栈的性质，出栈操作将在栈顶高度再次小于当前高度时停止，这时已经出栈的矩形已经完成了计算，它们的高度信息已失去作用，我们直接将新矩形的延伸看作一个完整的矩形并将其入栈，如图：

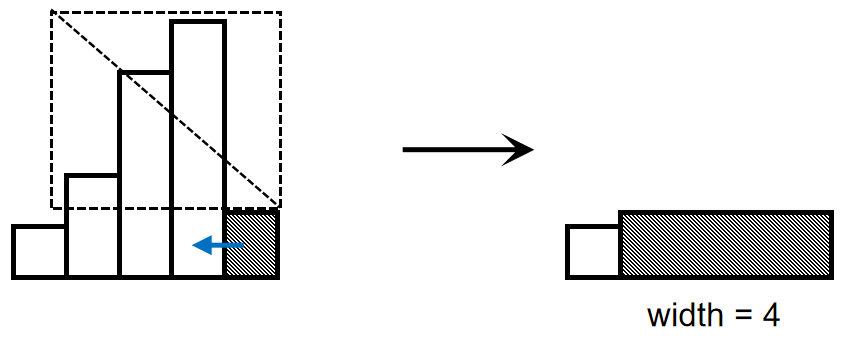
这样，在后续再次执行出栈操作时，我们直接累加它的总宽度，即可将其看作整体而存在，如图：

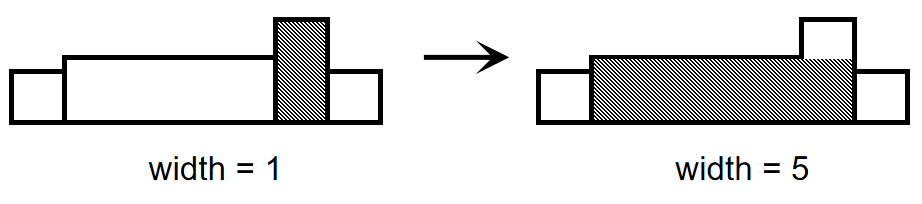
借助单调性处理问题的思想在于及时排除不可能的选项，保持策略集合的高度有效性和秩序性

实现：

while ((cin >> n) && n) {
p = -1, a[n] = ans = 0; // 1. 2.
for (int i = 0; i <= n; i++) {
  if (i != n) cin >> a[i];
  if (p == -1 || a[i] >= s[p])
    s[++p] = a[i], w[p] = 1; // 3.
  else {
    int width = 0;
    while (p != -1 && s[p] > a[i]) {
      width += w[p];
      ans = max(ans, (long long)s[p--] * width);
    }
    s[++p] = a[i], w[p] = width + 1;
  }
}
cout << ans << endl;

细节：

1. 只有当当前高度小于栈顶时才会触发答案的更新，因此，当所有高度遍历完成后，答案并不会自发地完成所有的更新。为了触发答案更新，我们可以在最后添加一个高度为0的柱子，以便在最后对所有的答案进行更新，如图：

   

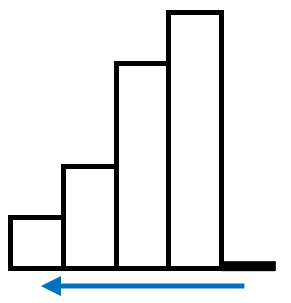
2. 尽管是取最大值，ans需初始化为0以应对最终答案为0的情形

3. w[]与s[]同步变化，类似于用多个数组来维护对象的不同属性，即可将s[i]看作a[i].h，w[i]看作a[i].w