树链剖分 求 最近公共祖先（LCA)

该文章用于记录个人在学习算法中的笔记

最近公共祖先问题（LCA）

        该问题是树论基本问题之一。

        求树上两点p和q的最近公共祖先，就是求在p和q的所有公共祖先中，离根最远的那个（又称为深度最大的那个）节点。注：p和q的最近公共祖先也有可能是p或q本身。

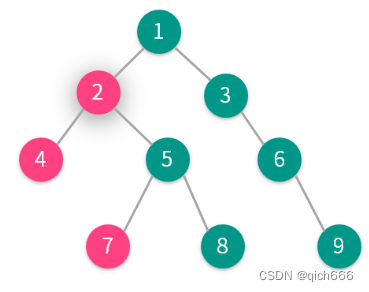
上图中，点4与点7的最近公共祖先为点2。

---

树链剖分（重链剖分）

        我将一步步分析该算法的具体原理（个人向）

1. 将树拆分为链

        该算法的核心思想是将一棵树拆解成若干条链。

        假设我们对一棵树进行了如下的刨分。

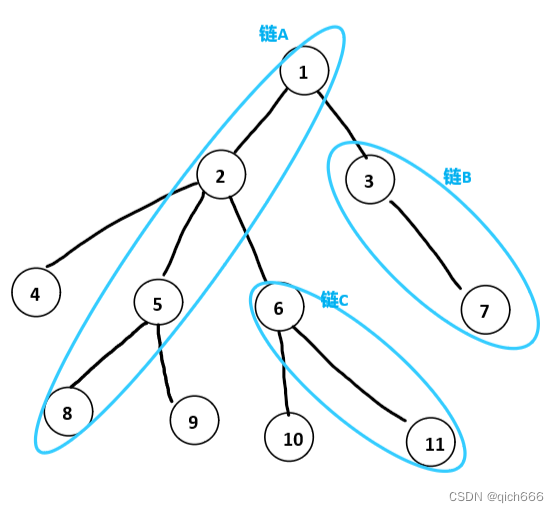
        我们将这棵树拆分成了一共有三条长度大于1的链（链ABC），另外该图中未被划分进链中的单独节点我们也可以视为他是一个长度为1的链。

进行了拆分后我们可以得知到什么信息？

        1）如果两个点都处于同一条链上，那么他们的最近公共祖先就是他们两个点中深度最小的那个。

        例如上图中的点8和点2，他们属于同一个链（链A），所以他们的最近公共祖先就是深度最小的点2。

         2）如果两个点不处于同一个链上，那么其所在链的头部深度较大的那个节点可以跳跃到他所在链的头部， 然后再往上跳跃一步就会进入另外一条链中，重复此做可以把情况转变为1）。

        这一点可能有点难以理解。我们还是举例说明。

        例如上图中，我们需要求解点5和点11的最近公共祖先。

        我们发现点5和点11不在同一条链上，且点11的深度更大。那么我们可以让点11直接跳跃到他所在链（链C）的头部，即点6。此时只需要再往上跳跃一步，就一定能进入新的一条链（链A）中。此时我们停留在点2上。

        做完如上跳跃操作后的新点就可以代替点11，我们的问题可以转变为求点5与点2的最近公共祖先。由1）可知，点5与点2在同一条链上，所以深度较小的点2是最近公共祖先。

        于是我们便找到了点11和点5的最近公共祖先，即点2。

        为什么要强调是  “所在链的头部深度较大”  的节点进行向上跳跃？

        想象一下上述例子中，我们如果先跳跃了点5，将其跳跃到了链A的头部，即点1上。

        由于还是不在同一条链上，我们还会继续进行跳跃，由于点1无法向上再跳，我们只能跳点11，将其跳到了点2上。

        现在我们发现点1和点2是在同一条链上，于是我们得出结果：深度最小的节点。这边我们得到了错误的结论“点1是点5和点11的最近公共祖先”。

        所以，如果不强调“所在链的头部深度较大”  的节点进行向上跳跃，我们可能会直接跳跃过正确结果，得出错误结论。可以理解为，我们尽可能的要少跳一点，以防错过正解。

2. 如何进行拆分

        我们知道了可以通过把树拆分为链的方式来寻找最近公共祖先。

        现在的问题变成，我们如何对一棵树进行拆分，使得最终的效果最好。

        想象一下如果我们只是随意的进行拆分，极端情况下，我们认为每个点都是一个各自的一条长为1的链，那么我们通过上述跳跃方法进行求解最近公共祖先问题时，我们每步跳跃都只会跳跃一个节点的距离。那么我们的这种算法和一步步向上求解的暴力做法无异。

        所以我们希望每条链都尽可能的长。这样每次跳跃就可以多跳跃几个节点。

        链尽可能长也就代表节点需要足够的多，所以我们在建链的时候可以尽量选择其子树最大的节点。

        下面引入几个概念

重儿子

我们对上面的树做了如下处理

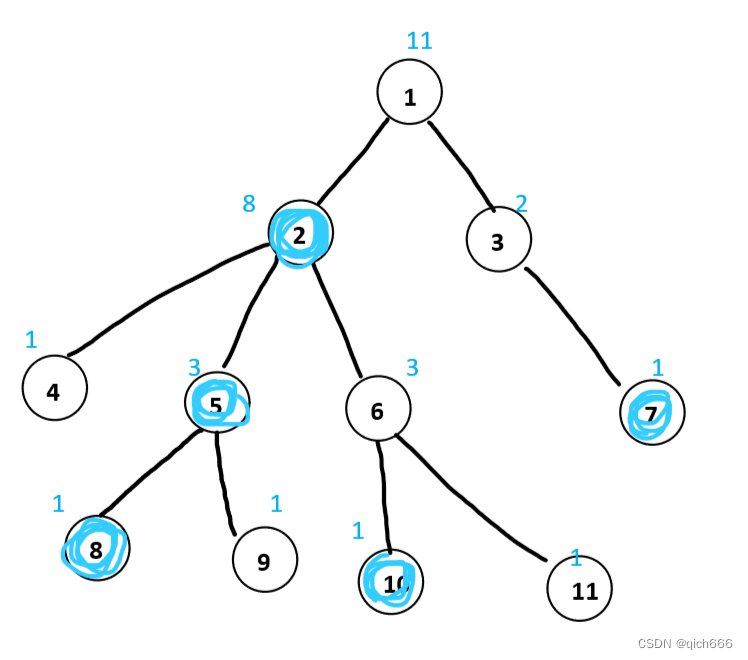
        我们算出了以所有节点为根的子树大小，标注在了节点上方（蓝色字）。

        然后对于每个节点，我们考虑：在所有他的儿子节点中，找到子树大小最大的节点（相同选择其中一个即可），标注出来（标为了蓝色），称其为重儿子。注：每个节点只能有一个重儿子。

重边、重链

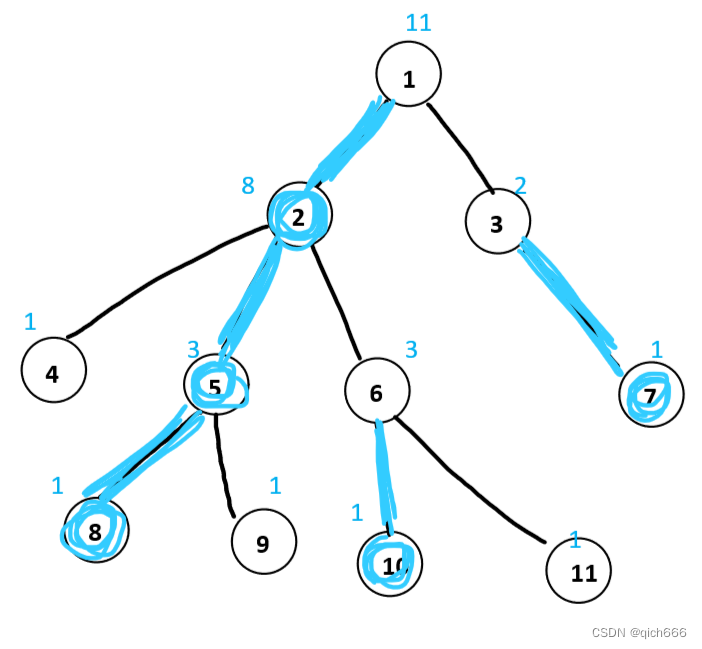
        我们把所有重儿子连接他的父亲节点的边成为重边（图中标蓝的边）。而所有重边构成的链就是重链。单独节点也可看为是一个长度为1的重链。

        如此做我们就完成了对整棵树的剖分。由于我们规定：重儿子是子树最大的子节点。所以我们可以保证所组成的重链足够长，且沿着重链向上每跳跃一步都能略过至少一半的节点。

        相对应的，不是重边的其他边我们称之为轻边。

---

3. 具体实现

        有了以上思考过程，我们就可以开始coding了。

        总结我们所需要的所有参数：

        fa[x]：记录点x的父亲节点

        dep[x]：记录点x的深度

        siz[x]：记录以点x为根的子树大小

        son[x]：记录点x的重儿子

        top[x]：记录点x所在重链的头节点

---

第一次预处理DFS1

对于fa[x]、dep[x]、siz[x]、son[x]信息我们可以用一次预处理实现：

void dfs1(int u) {
  son[u] = -1;
  siz[u] = 1;             //节点u的子树至少包含他自己
  dep[u] = dep[fa[u]] +1;  //记录深度
  for (int e = firste[u]; e!=0; e = nexte[e])  //链式前向星遍历边，可以用自己喜欢的方式更改
    int v = end[e];             //链式前向星 获得边终点
    if (v!=fa[u]) {                  
      fa[v] = u;                //记录父节点
      dfs1(v);                  //递归
      siz[u] += siz[v];         //递归结束后 把儿子的子树大小添加到点u的子树大小中
      if (son[u] == -1 || siz[v] > siz[son[u]]) son[u] = v;   //更新重儿子
    }
}

第二次预处理DFS2

 有了如上信息，我们可以求出各重链的头结点

void dfs2(int u, int t) {    //当前dfs的节点为u，当前重链的头节点为t
  top[u] = t;                //记录重链头节点

  //----------DFS序内容可以添加在这里------------

  if (son[u] == -1) return;  //递归结束

  dfs2(son[u], t);           //优先对重儿子进行 DFS
  for (int e = firste[u]; e!=0; e = nexte[e]){  //链式前向星遍历
    int v = end[e];
    if (v != son[u] && v != fa[u]) dfs2(v, v);
  }  //递归
}

查找最近公共祖先LCA 

        同上述思路一样，对于所在重链头节点深度更小的节点 进行向上跳跃的操作。 一次跳跃为：跳到所在重链头结点，然后再往上跳跃一次，到新重链。

        直到两点处于同一重链，返回深度较小的节点。

int lca(int a, int b) {
  while (top[a] != top[b]) {         //一直跳跃到a和b在同一条链上
    if (dep[top[a]] > dep[top[b]])   //重链头节点深度大的先跳
      a = fa[top[a]];                //跳到所在重链头节点后再向上跳跃一次
    else
      b = fa[top[b]];
  }
  return dep[a] < dep[b] ? a : b;
}

---

时间复杂度分析

两次预处理都使用了DFS，都需要遍历各个节点，O(n)

单次查询LCA，从根节点到各个节点的路径上至多经过logn个重链，O(logn)

综上，树链剖分的时间复杂度为O(n+logn) 其中预处理为O(n)，查询为O(logn)

树链剖分的常数十分小，很难被卡掉。

---

拓展

因为树链刨分可以保证划分出的每条链上的节点 DFS 序连续，因此可以方便地用一些维护序列的数据结构（如线段树）来维护树上路径的信息。

俺还没学到这么多T_T

---

LCA的价值

目前以我个人浅薄的算法积累来说，在树论中有很多算法都需要用到LCA，例如：树上前缀和、树上差分、Kruskal重构树等。

洛谷P3379【模板】最近公共祖先 完整代码

洛谷P3379

#include <bits/stdc++.h>
using namespace std;
#define endl '\n'

const int MAXN = 5e5+20,MAXM = 1e6+20;
int N,M,S;

int firste[MAXN],nexte[MAXM],eend[MAXM];
int cnt = 1;
void addEdge(int u,int v){
    nexte[cnt] = firste[u];
    eend[cnt] = v;
    firste[u] = cnt++;
}


int fa[MAXN],dep[MAXN],siz[MAXN],son[MAXN],top[MAXN];
void dfs1(int u){
    son[u] = -1;
    siz[u] = 1;
    dep[u] = dep[fa[u]] +1;
    for(int e=firste[u];e;e=nexte[e]){
        int v = eend[e];
        if(v!=fa[u]){
            fa[v] = u;
            dfs1(v);
            siz[u] +=siz[v];
            if(son[u]==-1||siz[v]>siz[son[u]]) son[u] = v;
        }
    }
}

void dfs2(int u, int t){
    top[u] = t;

    if(son[u]==-1) return;
    dfs2(son[u],t);
    for(int e=firste[u];e;e=nexte[e]){
        int v = eend[e];
        if(v!=son[u]&&v!=fa[u]) dfs2(v,v);
    }
}

int lca(int a,int b){
    while(top[a]!=top[b]){
        if(dep[top[a]]>dep[top[b]]){
            a = fa[top[a]];
        }
        else{
            b = fa[top[b]];
        }
    }
    return dep[a]<dep[b]? a:b;
}

signed main(){

    cin>>N>>M>>S;
    for(int i=1;i<N;i++) {
        int u,v;
        cin>>u>>v;
        addEdge(u,v); addEdge(v,u);
    }

    
    dfs1(S);
    dfs2(S,S);

    for(int i=1;i<=M;i++){
        int a,b;
        cin>>a>>b;
        cout<<lca(a,b)<<endl;
    }

    return 0;
}