指数平滑算法主要是为了预测一组数据后面若干值。
主要公式:
t=a*yt+(1-a)*St-1 式中,
St--时间t的平滑值;
yt--时间t的实际值;
St-1--时间t-1的平滑值;
a--平滑常数,其取值范围为[0,1]
一次平滑
yt+1'=a*yt+(1-a)*yt' 直接按照公式计算就可以
二次平滑
需要在一次平滑的基础上算出所有数据再平滑一次的结果
再代入数学模型算出a(和取值a不同)和b
三次平滑
思路和二次平滑差不多,在二次平滑数组的基础上,加一次平滑得到一组新的数据
代入数学模型算出a,b和c
/**
* 指数平滑算法
* @param array $datas 数据样本 [225.2,249.9,263.2,293.6,318.9,356.7,363.3,424.4,466.5,582,750]
* @param int $a 平滑常数,其取值范围为[0,1],指数平滑法对实际序列具有平滑作用,权系数(平滑系数) 越小,平滑作用越强,但对实际数据的变动反应较迟缓。
* @param int $step 后面n值,预测的数量
* @param int $n 平均值长度 平均值要大于数组长度
* @return array 预测数据
*/
function exp_smooth($data,$a=0.5,$step=3,$n=3){
$arr=$data;
$s0=0;
for ($i=0; $i < $n; $i++) {
$sum+=$arr[$i];
}
$s0=round($sum/$n,2);
$one_num[]=$s0;
//一次平滑
foreach ($arr as $k => $v) {
$one_num[]=round($a*$v,2)+round((1-$a)*$one_num[$k],2);
}
unset($one_num[0]);
$one_num=array_values($one_num);
$count=count($arr);
//二次平滑
$two_num[]=$one_num[0];
for ($i=1; $i < count($one_num); $i++) {
$two_num[]=round($a*$one_num[$i],2)+round((1-$a)*$two_num[$i-1],2);
}
unset($two_num[0]);
$two_num=array_values($two_num);
/* $e_arr=[];
$two_a=round(2*$one_num[$count-1]-$two_num[$count-2]);
$two_b=($a/(1-$a))*($one_num[$count-1]-$two_num[$count-2]);
for ($i=0; $i <$step ; $i++) {
$j=$i+1;
$e_arr[]=$two_a+round($j*$two_b,2);
}
return $e_arr;*/
//三次平滑
$three_num[]=$two_num[0];
for ($i=1; $i < count($one_num)-1; $i++) {
$three_num[]=round($a*$two_num[$i])+round((1-$a)*$three_num[$i-1],2);
}
unset($three_num[0]);
$three_num=array_values($three_num);
$three_a=3*$one_num[$count-1]-3*$two_num[$count-2]+$three_num[$count-3];
$three_b=round($a/(2*(1-$a)*(1-$a))*((6-5*$a)*$one_num[$count-1]-2*(5-4*$a)*$two_num[$count-2]+(4-3*$a)*$three_num[$count-3]),2);
$three_c=round($a*$a/(2*(1-$a)*(1-$a))*($one_num[$count-1]-2*$two_num[$count-2]+$three_num[$count-3]),2);
$t_arr=[];
for ($i=0; $i <$step ; $i++) {
$j=$i+1;
$t_arr[]=$three_a+$three_b*$j+$three_c*$j*$j;
}
return $t_arr;
}如若有误或者有其他问题请与我交流:2359582968(微信qq同号)










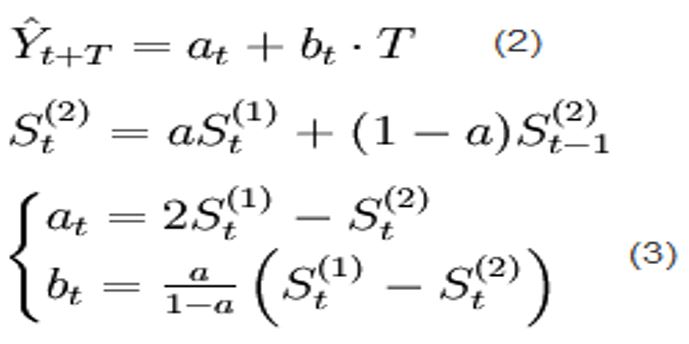
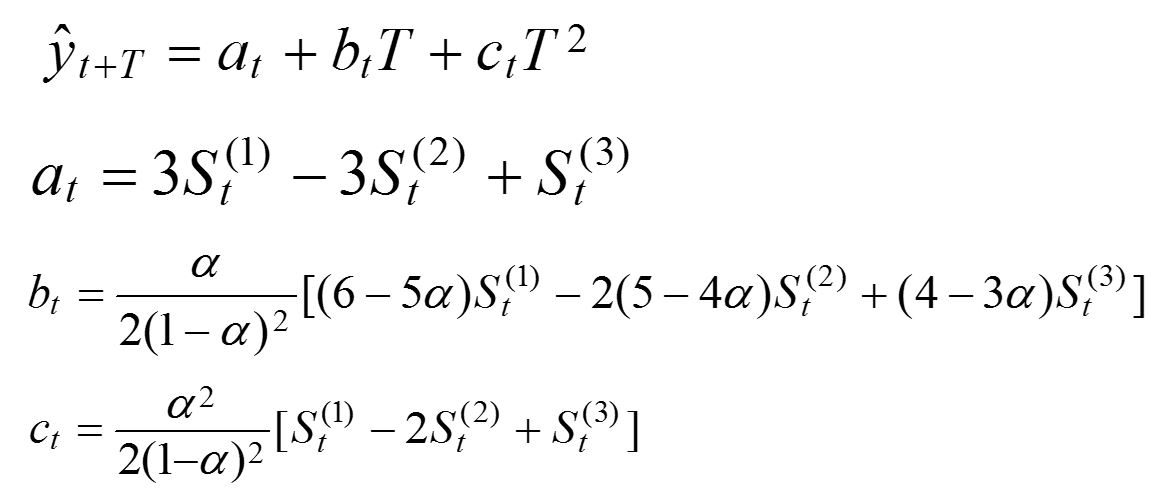














 71
71

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








