优化算法总结

最新推荐文章于 2024-03-27 15:52:49 发布

沐雨金鳞

最新推荐文章于 2024-03-27 15:52:49 发布

阅读量2k

点赞数

分类专栏： Machine learning 文章标签：优化算法总结

本文链接：https://blog.csdn.net/qq_38262266/article/details/102717576

版权

Machine learning 专栏收录该内容

32 篇文章 2 订阅

订阅专栏

好久就想写一篇有关优化算法的文章，今天下定决心一定要把优化算法弄的明明白白。

一、梯度

想学习优化算法首先就要知道什么是梯度。

1、微积分中：梯度表示函数增长最快的方向。神经网络中：采用负梯度表示目标函数下降最快的方向。

2、梯度仅仅指示了每个参数各自增长最快的方向，仅对每个参数而言，无法保证方向是全局最大(小)的方向。

3、梯度具体的计算方法：反向传播。

4、参数(负)梯度的大小表明参数对函数值变化的影响程度。

二、基本梯度下降->全部训练样本的平均损失

通过计算参数的梯度，从而更新参数，不断迭代，以使得目标函数达到最值的方法为梯度下降法。

1、梯度下降是一种优化算法，通过迭代寻找模型的最优参数。

2、最优参数：使目标函数达到最小值的参数。

3、目标函数是凸函数时，梯度下降的解=全局最优解。一般情况下不是。

4、缺点：1、每次更新参数遍历所有数据。2、训练样本量大时，耗费大量计算资源。

5、案例：

'''
一维梯度下降法示例
目标函数为：f(x) = x^2 + 1
当x为0时，目标函数取值最小
'''

# 目标函数
def func_1d(x):
    return x ** 2 + 1

# 目标函数梯度
def grad_1d(x):
    return x * 2

# 梯度下降法
def gradient_descent_1d(grad, cur_x=1, learning_rate=0.01, precision=0.0001, max_iters=10000):
    '''
    :param grad: 目标函数梯度
    :param cur_x: 当前x值
    :param learning_rate: 学习旅
    :param precision:  收敛精度
    :param max_iters:  最大迭代次数
    :return:  局部最小值
    '''
    for i in range(max_iters):
        grad_cur = grad(cur_x)
        # 当梯度趋于0时，视为收敛
        if abs(grad_cur) < precision:
            break
        cur_x = cur_x - grad_cur * learning_rate
        print('第',i,'次迭代：x值为：',cur_x)

gradient_descent_1d(grad_1d, cur_x=10, learning_rate=0.2, precision=0.000001, max_iters=10000)

第 0 次迭代：x值为： 6.0
第 1 次迭代：x值为： 3.5999999999999996
第 2 次迭代：x值为： 2.1599999999999997
第 3 次迭代：x值为： 1.2959999999999998
第 4 次迭代：x值为： 0.7775999999999998
第 5 次迭代：x值为： 0.46655999999999986
第 6 次迭代：x值为： 0.2799359999999999
第 7 次迭代：x值为： 0.16796159999999993
第 8 次迭代：x值为： 0.10077695999999996
第 9 次迭代：x值为： 0.06046617599999997
第 10 次迭代：x值为： 0.036279705599999976
第 11 次迭代：x值为： 0.021767823359999987
第 12 次迭代：x值为： 0.013060694015999992
第 13 次迭代：x值为： 0.007836416409599995
第 14 次迭代：x值为： 0.004701849845759997
第 15 次迭代：x值为： 0.002821109907455998
第 16 次迭代：x值为： 0.0016926659444735988
第 17 次迭代：x值为： 0.0010155995666841593
第 18 次迭代：x值为： 0.0006093597400104956
第 19 次迭代：x值为： 0.0003656158440062973
第 20 次迭代：x值为： 0.0002193695064037784
第 21 次迭代：x值为： 0.00013162170384226703
第 22 次迭代：x值为： 7.897302230536021e-05
第 23 次迭代：x值为： 4.7383813383216124e-05
第 24 次迭代：x值为： 2.8430288029929674e-05
第 25 次迭代：x值为： 1.7058172817957805e-05
第 26 次迭代：x值为： 1.0234903690774682e-05
第 27 次迭代：x值为： 6.1409422144648085e-06
第 28 次迭代：x值为： 3.684565328678885e-06
第 29 次迭代：x值为： 2.210739197207331e-06
第 30 次迭代：x值为： 1.3264435183243986e-06
第 31 次迭代：x值为： 7.958661109946391e-07
第 32 次迭代：x值为： 4.775196665967835e-07

'''
二维梯度下降法示例
目标函数为：f(x) = -e^(-(x^2+y^2))
当x为0,y为0时，目标函数取值最小
'''

import math
import numpy as np

# 目标函数
def func_2d(x):
    return -math.exp(-(x[0]**2 + x[1]**2))

# 目标函数的梯度
def grad_2d(x):
    deriv0 = 2 * x[0] * math.exp(-(x[0]**2 + x[1]**2))
    deriv1 = 2 * x[1] * math.exp(-(x[0]**2 + x[1]**2))
    return np.array([deriv0, deriv1])

def gradient_descent_2d(grad, cur_x=np.array([0.1,0.1]), learning_rate=0.01, precision=0.0001, max_iter=10000):
    print(f'{cur_x}作为初始值开始迭代...')
    for i in range(max_iter):
        grad_cur = grad(cur_x)
        # 范数：两个值的平方和的平方根
        if np.linalg.norm(grad_cur, ord=2) < precision:
            break
        cur_x = cur_x - grad_cur * learning_rate
        print('第',i,'次迭代的值为',cur_x)
    print('局部最小值为：',cur_x)
    return cur_x

gradient_descent_2d(grad_2d, cur_x=np.array([1,-1]), learning_rate=0.2, precision=0.000001, max_iter=10000)

[ 1 -1]作为初始值开始迭代...
第 0 次迭代的值为 [ 0.94586589 -0.94586589]
第 1 次迭代的值为 [ 0.88265443 -0.88265443]
第 2 次迭代的值为 [ 0.80832661 -0.80832661]
第 3 次迭代的值为 [ 0.72080448 -0.72080448]
第 4 次迭代的值为 [ 0.61880589 -0.61880589]
第 5 次迭代的值为 [ 0.50372222 -0.50372222]
第 6 次迭代的值为 [ 0.3824228 -0.3824228]
第 7 次迭代的值为 [ 0.26824673 -0.26824673]
第 8 次迭代的值为 [ 0.17532999 -0.17532999]
第 9 次迭代的值为 [ 0.10937992 -0.10937992]
第 10 次迭代的值为 [ 0.06666242 -0.06666242]
第 11 次迭代的值为 [ 0.04023339 -0.04023339]
第 12 次迭代的值为 [ 0.02419205 -0.02419205]
第 13 次迭代的值为 [ 0.01452655 -0.01452655]
第 14 次迭代的值为 [ 0.00871838 -0.00871838]
第 15 次迭代的值为 [ 0.00523156 -0.00523156]
第 16 次迭代的值为 [ 0.00313905 -0.00313905]
第 17 次迭代的值为 [ 0.00188346 -0.00188346]
第 18 次迭代的值为 [ 0.00113008 -0.00113008]
第 19 次迭代的值为 [ 0.00067805 -0.00067805]
第 20 次迭代的值为 [ 0.00040683 -0.00040683]
第 21 次迭代的值为 [ 0.0002441 -0.0002441]
第 22 次迭代的值为 [ 0.00014646 -0.00014646]
第 23 次迭代的值为 [ 8.78751305e-05 -8.78751305e-05]
第 24 次迭代的值为 [ 5.27250788e-05 -5.27250788e-05]
第 25 次迭代的值为 [ 3.16350474e-05 -3.16350474e-05]
第 26 次迭代的值为 [ 1.89810285e-05 -1.89810285e-05]
第 27 次迭代的值为 [ 1.13886171e-05 -1.13886171e-05]
第 28 次迭代的值为 [ 6.83317026e-06 -6.83317026e-06]
第 29 次迭代的值为 [ 4.09990215e-06 -4.09990215e-06]
第 30 次迭代的值为 [ 2.45994129e-06 -2.45994129e-06]
第 31 次迭代的值为 [ 1.47596478e-06 -1.47596478e-06]
第 32 次迭代的值为 [ 8.85578865e-07 -8.85578865e-07]
第 33 次迭代的值为 [ 5.31347319e-07 -5.31347319e-07]
第 34 次迭代的值为 [ 3.18808392e-07 -3.18808392e-07]
局部最小值为： [ 3.18808392e-07 -3.18808392e-07]

可以发现，如果将初始值设置为：[3, -3]

[ 3 -3]作为初始值开始迭代...
局部最小值为： [ 3 -3]

这就是梯度下降法的缺点所在，当目标函数是凸函数时，梯度下降法的解才是全局最优解。

三、随机梯度下降(SGD)->单个训练样本的损失

背景：基本梯度下降法采用所有训练样本的平均损失来更新参数。

SGD：每次使用单个样本的损失来代替平均损失。

缺点：每次使用一个训练样本的损失，方差大，迭代不稳定。

四、小批量梯度下降->一批训练样本的损失

背景：基本梯度下降的缺点、SGD缺点。

方法：使用一批随机训练样本的损失代替平均损失。

其他目的：利用高度优化的矩阵运算和并行计算框架。

更新过程：

在训练集上抽取指定大小（batch_size）的一批数据 {(x,y)}
【前向传播】将这批数据送入网络，得到这批数据的预测值 y_pred
计算网络在这批数据上的损失，用于衡量 y_pred 和 y 之间的距离
【反向传播】计算损失相对于所有网络中可训练参数的梯度 g
将参数沿着负梯度的方向移动，即 W -= lr * g

‘批’的大小对优化结果的影响：

较大的批能得到更精确的梯度估计。
较小的批能带来更好的泛化误差，泛化误差通常在批大小为 1 时最好。
- 原因可能是由于小批量在学习过程中带来了噪声，使产生了一些正则化效果 (Wilson and Martinez, 2003)
- 但是，因为梯度估计的高方差，小批量训练需要较小的学习率以保持稳定性，这意味着更长的训练时间。
当批的大小为 2 的幂时能充分利用矩阵运算操作，所以批的大小一般取 32、64、128、256 等。

五、梯度下降存在什么问题

随机梯度下降（SGD）放弃了梯度的准确性，仅采用一部分样本来估计当前的梯度；因此 SGD 对梯度的估计常常出现偏差，造成目标函数收敛不稳定，甚至不收敛的情况。
无论是经典的梯度下降还是随机梯度下降，都可能陷入局部极值点；除此之外，SGD 还可能遇到“峡谷”和“鞍点”两种情况
- 峡谷类似一个带有坡度的狭长小道，左右两侧是“峭壁”；在峡谷中，准确的梯度方向应该沿着坡的方向向下，但粗糙的梯度估计使其稍有偏离就撞向两侧的峭壁，然后在两个峭壁间来回震荡。
- 鞍点的形状类似一个马鞍，一个方向两头翘，一个方向两头垂，而中间区域近似平地；一旦优化的过程中不慎落入鞍点，优化很可能就会停滞下来。

六、改进方法

SGD改进的两个方向：惯性保持和环境感知。

惯性保持：加入动量的SGD算法。

环境感知：根据不同参数的一些经验性判断，自适应的确定每个参数的学习速率。

七、动量(Momentum)算法之带动量的SGD

引入动量（Momentum）方法一方面是为了解决“峡谷”和“鞍点”问题。

一方面也可以用于SGD 加速，特别是针对高曲率、小幅但是方向一致的梯度。

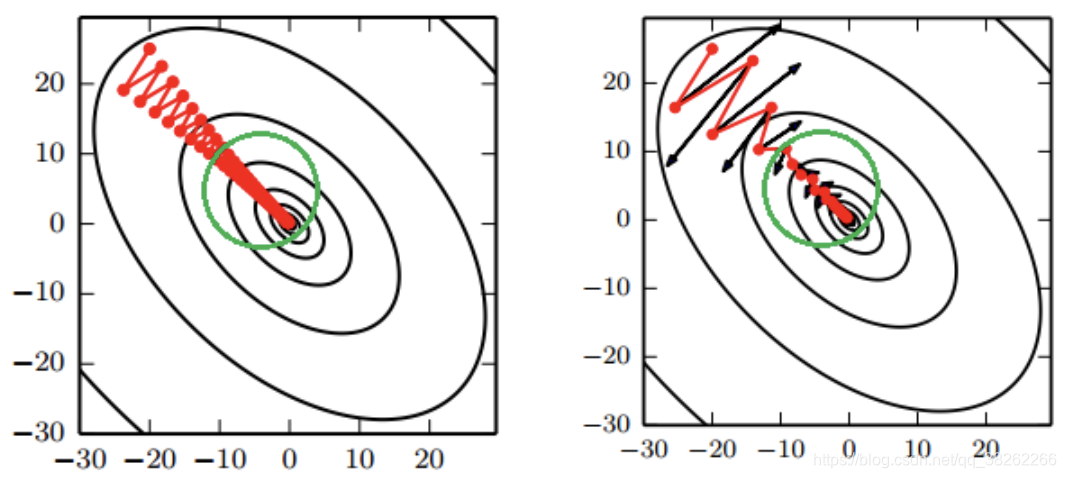
如果把原始的 SGD 想象成一个纸团在重力作用向下滚动，由于质量小受到山壁弹力的干扰大，导致来回震荡；或者在鞍点处因为质量小速度很快减为 0，导致无法离开这块平地。
动量方法相当于把纸团换成了铁球；不容易受到外力的干扰，轨迹更加稳定；同时因为在鞍点处因为惯性的作用，更有可能离开平地。
动量方法以一种廉价的方式模拟了二阶梯度（牛顿法）

参数更新公式：

从形式上看，动量算法引入了变量 v 充当速度角色，以及相相关的超参数 α。
原始 SGD 每次更新的步长只是梯度乘以学习率；现在，步长还取决于历史梯度序列的大小和排列；当许多连续的梯度指向相同的方向时，步长会被不断增大；

动量算法描述：

如图所示：其实就是在原有的梯度更新的基础上增加了a和v两个参数，用来控制梯度更新的速度。

如果动量算法总是观测到梯度 g，那么它会在 −g 方向上不断加速，直到达到最终速度。

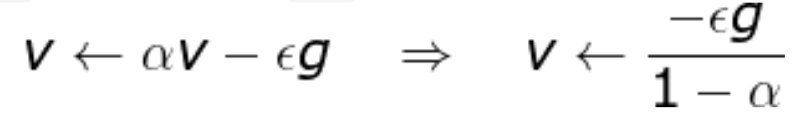
在实践中， α 的一般取 0.5, 0.9, 0.99，分别对应最大 2 倍、10 倍、100 倍的步长
和学习率一样，α 也可以使用某种策略在训练时进行自适应调整；一般初始值是一个较小的值，随后会慢慢变大。

八、动量算法之NAG算法(Nesterov动量)

NAG 把梯度计算放在对参数施加当前速度之后。
这个“提前量”的设计让算法有了对前方环境“预判”的能力。Nesterov 动量可以解释为往标准动量方法中添加了一个修正因子。
NAG 算法描述

如图所示，在动量算法的基础上，更新参数前的速度计算中的梯度并不是原梯度，而是经过参数临时更新后重新计算出的梯度。

九、自适应学习率的优化算法之AdaGrad-2011

该算法的思想是独立地适应模型的每个参数：具有较大偏导的参数相应有一个较大的学习率，而具有小偏导的参数则对应一个较小的学习率。

具体来说，每个参数的学习率会缩放各参数反比于其历史梯度平方值总和的平方根。

AdaGrad 算法描述：

注意：全局学习率 ϵ 并没有更新，而是每次应用时被缩放。

AdaGrad 存在的问题：

学习率是单调递减的，训练后期学习率过小会导致训练困难，甚至提前结束。
需要设置一个全局的初始学习率。

十、自适应学习率的优化算法之RMSProp-2012

RMSProp 主要是为了解决 AdaGrad 方法中学习率过度衰减的问题—— AdaGrad 根据平方梯度的整个历史来收缩学习率，可能使得学习率在达到局部最小值之前就变得太小而难以继续训练；

RMSProp 使用指数衰减平均（递归定义）以丢弃遥远的历史，使其能够在找到某个“凸”结构后快速收敛；此外，RMSProp 还加入了一个超参数 ρ 用于控制衰减速率。

具体来说（对比 AdaGrad 的算法描述），即修改 r 为：

其中 E 表示期望，即平均；δ 为平滑项，具体为一个小常数，一般取 1e-8 ~ 1e-10（Tensorflow 中的默认值为 1e-10）。

RMSProp 建议的初始值：全局学习率 ϵ=1e-3，衰减速率 ρ=0.9。

RMSProp 算法描述：

带 Nesterov 动量的 RMSProp：

经验上，RMSProp 已被证明是一种有效且实用的深度神经网络优化算法。

RMSProp 依然需要设置一个全局学习率，同时又多了一个超参数（推荐了默认值）。

先写到这里，以后再加...

沐雨金鳞

关注

0
点赞
踩
18

收藏

觉得还不错? 一键收藏
0
评论
优化算法总结

好久就想写一篇有关优化算法的文章，今天下定决心一定要把优化算法弄的明明白白。一、梯度想学习优化算法首先就要知道什么是梯度。1、微积分中：梯度表示函数增长最快的方向。神经网络中：采用负梯度表示目标函数下降最快的方向。2、梯度仅仅指示了每个参数各自增长最快的方向，仅对每个参数而言，无法保证方向是全局最大(小)的方向。3、梯度具体的计算方法：反向传播。4、参数(负)梯度的大小表明...
复制链接

扫一扫