深度优先遍历
深度优先遍历(Depth-First Traversal)简称DFS。
算法思想:
- 首先以一个未被访问过的顶点作为起始顶点,沿当前顶点的边走到未访问过的顶点;
- 当没有未访问过的顶点时,则回到上一个顶点,继续试探别的顶点,直到所有的顶点都被访问过。
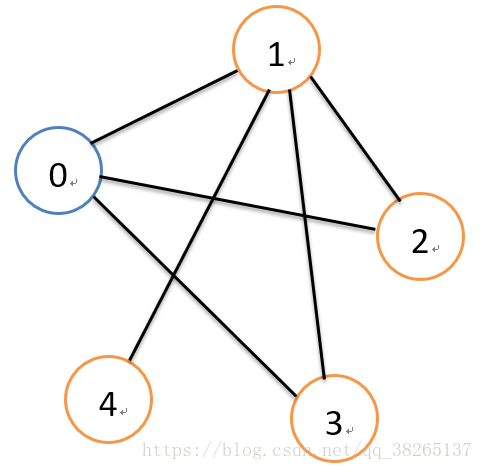
如上图,采用图的深度优先遍历的话,从0号节点遍历的顺序应该是:0,1,2,3,4.
程序源代码示例:
public class DeepTravel {
public static void main(String[] args) {
//图的邻接矩阵表示
int[][] a = {
{0,1,1,1,0},
{1,0,1,1,1},
{1,1,0,0,0},
{1,1,0,0,0},
{0,1,0,0,0}};
//需要一个数字,来记录染色信息,染色的节点代表已经遍历
int[] color = new int[a.length];
System.out.println("深度优先遍历的结果为:");
dfs(a, color, 0);
}
//用递归的方法进行遍历
private static void dfs(int[][] a, int[] color, int k) {
System.out.print(k + " ");//打印出k号节点
color[k] = 1;//给k号节点标记为1
for(int i = 0; i < a[k].length; i++)
if(a[k][i] == 1 && color[i] == 0)
dfs(a, color, i);
}
}程序运行结果:
深度优先遍历的结果为:
0 1 2 3 4 广度优先遍历
广度优先搜索算法(英语:Breadth-First-Search,缩写为BFS)。
其过程检验来说是对每一层节点依次访问,访问完一层进入下一层,而且每个节点只能访问一次。
程序示例:
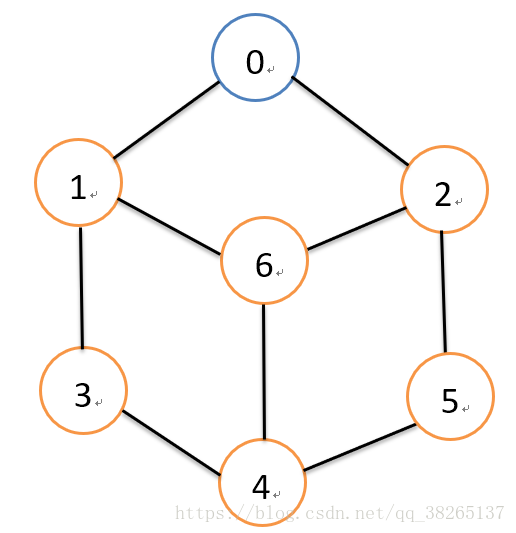
如上图,,采用图的广度优先遍历的话,从0号节点遍历的顺序应该是:0,1,2,3,6,5,4
程序源代码:
import java.util.ArrayList;
import java.util.HashSet;
import java.util.Set;
public class BreadthTravel {
public static void main(String[] args) {
//图的邻接定义
int[][] g = {
{0,1,1,0,0,0,0},
{1,0,0,1,0,0,1},
{1,0,0,0,0,1,1},
{0,1,0,0,1,0,0},
{0,0,0,1,0,1,1},
{0,0,1,0,1,0,0},
{0,1,1,0,1,0,0}};
//广度优先遍历
System.out.println("广度优先遍历的结果:");
bfs(g);
}
private static void bfs(int[][] g) {
ArrayList<Integer> list = new ArrayList<Integer>();//等待遍历的节点
Set<Integer> set = new HashSet<Integer>();//已经遍历的节点
list.add(0);//从0号节点开始遍历
while (true) {
//如果列表为空,则遍历完成
if(list.isEmpty())
break;
int node = list.get(0);
System.out.print(node + " ");
set.add(node);
list.remove(0);
for(int i = 0; i < g[node].length; i++) {
if(g[node][i] == 1 && set.contains(i) == false && list.indexOf(i)<0)
list.add(i);
}
}
}
}程序运行结果:
广度优先遍历的结果:
0 1 2 3 6 5 4 最短路径树
迪杰斯特拉算法简介
迪杰斯特拉算法是由荷兰计算机科学家狄克斯特拉于1959 年提出的,因此又叫狄克斯特拉算法。是从一个顶点到其余各顶点的最短路径算法,解决的是有向图中最短路径问题。迪杰斯特拉算法主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止。
程序示例:
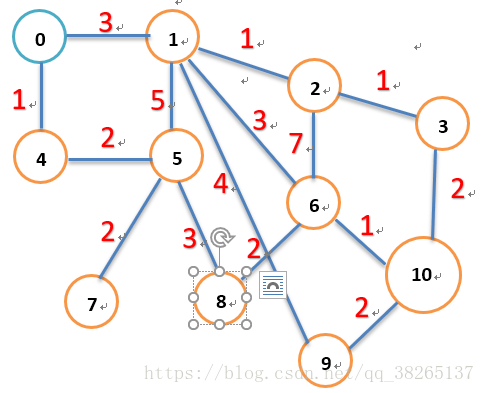
如上图,从求0号节点开始到所有节点的最短路径。
程序源代码:
import java.util.ArrayList;
import java.util.HashMap;
import java.util.Iterator;
import java.util.Map;
public class 最短路径树 {
static class Cell{
int node; //连接到哪个节点
int weight; //边的权值
public Cell(int node, int weight) {
this.node = node;
this.weight = weight;
}
}
@SuppressWarnings("unchecked")
public static void main(String[] args) {
//图的邻接表
ArrayList[] g = new ArrayList[11];
for(int i = 0; i < g.length; i++)
g[i] = new ArrayList();
g[0].add(new Cell(1, 3));
g[0].add(new Cell(4, 1));
g[1].add(new Cell(2, 1));
g[1].add(new Cell(6, 3));
g[1].add(new Cell(5, 5));
g[1].add(new Cell(0, 3));
g[1].add(new Cell(9, 4));
g[2].add(new Cell(1, 1));
g[2].add(new Cell(3, 1));
g[2].add(new Cell(6, 7));
g[3].add(new Cell(2, 1));
g[3].add(new Cell(10, 2));
g[4].add(new Cell(0, 1));
g[4].add(new Cell(5, 2));
g[5].add(new Cell(4, 2));
g[5].add(new Cell(1, 5));
g[5].add(new Cell(7, 2));
g[5].add(new Cell(8, 3));
g[6].add(new Cell(1, 3));
g[6].add(new Cell(2, 3));
g[6].add(new Cell(8, 2));
g[6].add(new Cell(10, 1));
g[7].add(new Cell(5, 2));
g[8].add(new Cell(5, 3));
g[8].add(new Cell(6, 2));
g[9].add(new Cell(1, 4));
g[9].add(new Cell(10, 2));
g[10].add(new Cell(3, 2));
g[10].add(new Cell(6, 1));
g[10].add(new Cell(9, 2));
//求0号节点开始的所有最小路径
Dijkstra(g);
}
public static void Dijkstra(ArrayList[] g) {
//节点号-->最小路径值
Map<Integer, Integer> map = new HashMap<Integer, Integer>();
while(true) {
int min = Integer.MAX_VALUE; //最小路径值
int min_no = -1; //对应的节点号
//所有与0号节点邻接,并且不在集合map中的点
for(int i = 0; i < g[0].size(); i++) {
Cell t = (Cell) g[0].get(i);
if(map.get(t.node) == null && t.weight < min) {
min_no = t.node;
min = t.weight;
}
}
//与map中点邻接的所有不在map中的点
Iterator it = map.keySet().iterator();
while(it.hasNext()) {
int k = (int)it.next();
//集合中的点对应的最小路径的值
int v = (int)map.get(k);
for(int i = 0; i < g[k].size(); i++) {
Cell t = (Cell)g[k].get(i);
if(map.get(t.node) == null && t.weight + v < min) {
min_no = t.node;
min = t.weight + v;
}
}
}
if(min < Integer.MAX_VALUE)
map.put(min_no, min);
else
break;
}
System.out.println(map);
}
}程序运行结果:
{0=2, 1=3, 2=4, 3=5, 4=1, 5=3, 6=6, 7=5, 8=6, 9=7, 10=7}






















 228
228











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








