带妹妹学密码系列三 ----分组密码（一）

橘橘的成长日记

已于 2022-07-29 19:41:20 修改

阅读量2.4k

点赞数 1

分类专栏：密码学分组密码文章标签：密码学分组密码

于 2022-07-29 00:05:09 首次发布

本文链接：https://blog.csdn.net/qq_38324605/article/details/125898322

版权

密码学同时被 2 个专栏收录

11 篇文章

订阅专栏

分组密码

2 篇文章

订阅专栏

本文介绍了分组密码的概念，包括其基本原理如代换、扩散与混淆，以及经典的Feistel加密结构。重点讨论了DES、AES和SM4这三种分组密码算法，并提到了分组密码的运行模式如ECB、CBC等。此外，还探讨了非平衡Feistel结构在应对大分组长度时的作用。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

带妹妹学密码系列三 ——分组密码（一）

经典密码：http://t.csdn.cn/bj95q。
分组密码算法（Block Cipher Algorithm）是将输入数据划成固定长度的组进行加密和解密的一类对称密码算法。安全性依赖于密钥安全，在这里我们将主要介绍DES,AES以及SM4算法

分组密码概述

利用分组密码对明文加密时，首先需要对明文进行分组，每组长度相同，然后最每组密文分别加密得到密文。在这里插入图片描述
其中，x为明文，k为密钥，y为密文。E为加密算法，D为解密算法。
注：分组密码与流密码均为对称密码，区别在于分组密码输出的每一位数字不是只与对应时刻输入的明文数字有关，而是与一组长为n的明文数字有关。通常x,y等长，在存在数据扩展与数据压缩的情况下数据不等。

分组密码基本原理

代换
定义：明文分组到密文分组的可逆变换称为代换
为了满足加密算法的可逆性，即加密后可正确解密，每组明文都会产生唯一的一组密文，这样的变换是可逆的。
典型代表：S盒
在这里插入图片描述
该S盒为DES使用的S盒，该S盒为DES算法中唯一的非线性部件，是整个算法的安全性所在。该S盒为6bit输入4bit输出的变换。若给定该S盒的输入 $b_{0}b_{1}b_{2}b_{3}b_{4}b_{5}$ ，其输出对应该矩阵第L行n列对应数的二进制数。L为由 $b_{0}b_{5}$ 形成的十进制数表示，n为由 $b_{1}b_{2}b_{3}b_{4}$ 形成的十进制数表示，这样每个S盒可用一个4×16矩阵来表示。例如， $S_{1}$ 的输入为011001，行选为01(第1行)，列选为1100(第12列)，行列交叉位置的数为9，其4位二进制数表示为1001，所以S的输出为1001。
扩散与混淆
目的：扩散(Diffusion)和混淆(Confusion)是由Shannon提出的设计密码系统的两种基本方法，目的是抗击攻击者对密码系统的统计分析。如果攻击者知道明文的某些统计特性，如消息中不同字母出现的频率、可能出现的特定单词或短语，而且这些统计特性以某种方式在密文中反映出来，那么攻击者就有可能得出加密密钥或其中一部分，或者得出包含加密密钥的一个可能的密钥集合。在被 Shannon称为理想密码的密码系统中，密文的所有统计特性都与所使用的密钥独立。
扩散：扩散是将明文的统计特性散布到密文中去，使明文的每位影响密文中多位的值，等价于密文中每位均受明文中多位的影响，即从密文中不能获得明文的统计特性。当然，理想的情况是让明文中的每位影响密文中的所有位，或者说让密文的每位受明文中的所有位的影响。
扩散的目的：使明文和密文之间的统计关系变得尽可能复杂，以使攻击者无法得到密钥。
混淆：使密文和密钥之间的统计关系变得尽可能复杂，以使攻击者无法得到密钥。

分组密码结构

Feistel加密结构
1：平衡的Feistel结构
在这里插入图片描述
设x为长度为2m的明文，其加密过程为：将x分为长度为m的两部分，分别记为 $L_{0},R_{0}$ ,即 $x=L_{0}R_{0}$ ，对于 $1\leqslant i\leqslant r$ 有：
$\left\{\begin{matrix} L_{i}=R_{i-1} \\ R_{i}=L_{i-1}\oplus F\left ( R_{i-1},K_{i} \right ) \end{matrix}\right.$
其中，F为一个加密函数，称为圈函数， $K_{i}$ 是由密钥K产生的长度为tbit的子密钥，r为迭代次数，最后密文为 $y=R_{r}L_{r}$ 。
解密过程为加密过程的逆过程。
2：非平衡的Feistel结构
Feistel结构同样存在弊端。众所周知，过去的分组密码都是64bit分组长度，而随着计算能力的提高，现在设计的分组密码都要求至少128bit分组长度。对于传统的Feistel网络，分组长度的增加意味着轮函数f规模的增加，而构造大规模的轮函数又是比较困难的，因此便提出了采用非平衡Feistel网络对较大的明文分组进行加密的方法。将明文分为n个运算字，进行n次迭代就能将明文全部覆盖一遍。

在这里插入图片描述
设x为长度为2m的明文，其加密过程为：将x分为长度为 $n_{1},n_{2}$ 的两部分,满足 $n_{1}+n_{2}=2m$ ，分别记为 $L_{0},R_{0}$ ,即 $x=L_{0}R_{0}$ ，对于 $1\leqslant i\leqslant r$ 有：
$\left\{\begin{matrix} X_{i}^{L}=R_{i-1} \\ X_{i}^{R}=L_{i-1}\oplus F\left ( R_{i-1},K_{i} \right ) \\ X_{i}=X_{i}^{L}X_{i}^{R} \end{matrix}\right.$
其中， $L_{i}$ 为 $n_{1}$ bit， $R_{i}$ 为 $n_{2}$ bit。 $K_{i}$ 是由密钥K产生的长度为tbit的子密钥，r为迭代次数；F为一个加密函数，称为圈函数,为 $GF(2)^n_{2}$ X $GF(2)^t$ 到 $GF(2)^n_{1}$ 的函数，最后密文为 $y=X_{r}^{L}X_{r}^{R}$ 。
Feistel型分组密码的优点是加密过程与解密过程相似。在Feistel型分组密码的加密过程的最后一轮没有进行“左右交换”，目的就是可以利用同一个算法来实现加密和解密。
第一种非平衡Feistel网络如图所示
在这里插入图片描述
第二种非平衡Feistel网络如图所示，SM4分组密码算法所采用的网络结构与第二种非平衡Feistel 网络类似。

SP网络

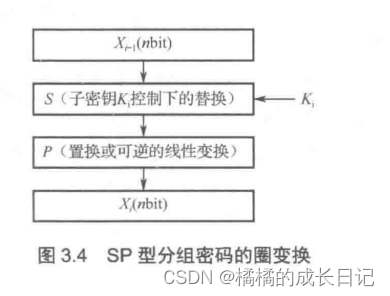
SP型分组密码的圈变换如图所示。其中，x为长度为nbit的明文， $K_{i}$ 为子密钥，首先对明文做非线性S变换，然后做线性变换P变换，共进行r轮迭代。在SP型分组密码中，代换S一般被称为混淆层，主要起混淆作用;置换或可逆的线性变换Р一般被称为扩散层，主要起扩散作用。
SP网络可以看作 Feistel网络的推广，但SP型分组密码的加密过程与解密过程一般不相似，即不能用同一个算法来实现加密和解密。（可以根据加解密过程是否相似来判断设计结构）
在后面章节中，我将介绍DES,AES以及SM4分组密码，欢迎指教！
补充：分组密码运行模式
分组密码在加密时，明文分组的长度是固定的，而在实际应用中待加密消息的数据量是不固定的，数据格式可能多种多样。为了能在各种应用场合使用DES，1980年NIST公布了DES的4种工作模式:电子密码本(Electronic Code Book，ECB)模式、密码分组链接(Cipher BlockChaining，CBC)模式、密码反馈(Cipher Feedback,CFB）模式和输出反馈(Output Feedback,OFB）模式。2000年3月，NIST为 AES公开征集工作模式，并在2001年12月公布了AES的5种工作模式，即 ECB、CBC、CFB、OFB和CTR（计数器模式，Counter Mode)。