数据分析中正态分布的作用
正态分布的作用
正态分布准确地说什么是标准离差?它用最标准方式表达的期望值(标准差)的离差。
第一步是收集一系列教据和决定你的期望值是多少。
例如找们讨论的抛两个般子的情况.你可能期望得到一个综合值等于7点的结果。然而你可能得到的不是7。我们抛般子50次并记录结果,最后得到期望分布。
再比如说你要对班级成绩的数据进行抽样调查,得到的就是班级成绩的一个整体分布,学的特别好的人肯定是少数,学的不好的人肯定也是少数,所有学的一般的肯定占据这个班上人数的一大半,所以在一个大的区间还是一个小的区间都是可以从一定的程度上反应出班级的整体的收教育的程度的。
如果得到的是这个班级的成绩主要都是在70到80分之间(100的满分),和主要成绩在60到90之间,这样就可以得到不同的结论。

从这样一个正态分布曲线,我们可以看出最高点就是这份数据的平均值,正态曲线的陡峭或扁平程度则是由标准差决定的,标准差越小,曲线越陡峭;标准差越大,曲线越扁平。
正态分布具有以下几个特性:
集中性:曲线的最高峰位于正中央,且位置为均数所在的位置。
对称性:正态分布曲线以均数所在的位置为中心左右对称且曲线两段无线趋近于横轴。
均匀变动性:正态分布曲线以均数所在的位置为中心均匀向左右两侧下降。
面积恒等:曲线与横轴间的面积总等于1。
正态分布公式详解

从公式上可以看出,正态分布有平均数和标准差决定的
这里提一个容易混淆的两个概念,平均值和期望,很多时候我们都会认为这是同一个东西,实际上平均值属于数理统计,期望则是属于概率论,但是二者都是对总体趋势的一种度量。
数学期望常称为“均值”,即“随机变量取值的平均值”之意,当然这个平均,是指以概率为权的加权平均。数学期望是由随机变量的分布完全决定。
大数定理:当样本量N趋近无穷大的时候,样本的平均值无限接近数学期望
标准正态分布面积比例计算
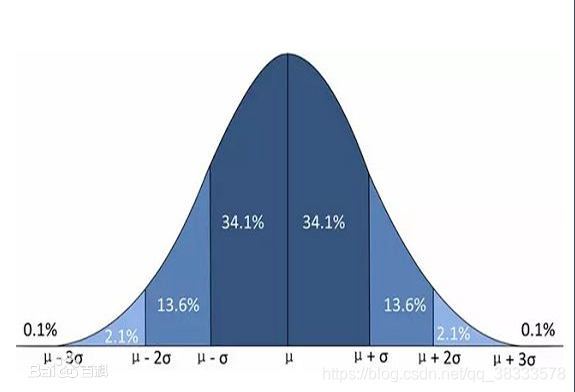

首先我们要知道的是轴与正态曲线之间的面积恒等于1,然后我们对x轴上的值做标准化处理
(x-均值)/标准差=x的标准化(标准正态分布的x值)。
然后将标准化的值拿到标准正态分布表里去查对应的值,最后1-表对应值得到x所占整个数据的比例。
标准正态分布是正态分布的一种,平均数为0,标准差为1。
中心极限定理
中心极限定理的概念:中心极限定理指的是给定一个任意分布的总体。我每次从这些总体中随机抽取 n 个抽样,一共抽 m 次。 然后把这 m 组抽样分别求出平均值。 这些平均值的分布接近正态分布。
举个简单的例子:现在我们要统计全国的人的成年男性身高,看看我国平均成年男性身高是多少。但是我们把全国所有人的成年男性身高都调查一遍是不现实的。所以我们打算一共调查1000组,每组50个人。 然后,我们求出第一组的成年男性身高平均值、第二组的成年男性身高平均值,一直到最后一组的成年男性身高平均值。
根据中心极限定理说:这些平均值是呈现正态分布的。并且,随着组数的增加,效果会越好。最后,当我们再把1000组算出来的平均值加起来取个平均值,这个平均值会接近全国平均成年男性身高。
中心极限定理有几点需要注意:总体本身的分布不要求正态分布,但是最后算出来的平均值却会接近正态。
还有就是样本每组要足够大,但也不需要太大,一般认为,每组大于等于30个,即可让中心极限定理发挥作用。
离散型随机变量与连续型随机变量
离散型随机变量与连续型随机变量都是由随机变量取值范围(取值)确定。
变量取值只能取离散型的自然数,就是离散型随机变量。例如,一次掷20个骰子,k个骰子面朝6,k是随机变量。k的取值只能是自然数0,1,2,…,20,而不能取小数3.5、无理数,因而k是离散型随机变量。
如果变量可以在某个区间内取任一实数,即变量的取值可以是连续的,这随机变量就称为连续型随机变量。例如,地铁每5分钟一班,某人在站台等车时间x是个随机变量,x的取值范围是[0,5),它是一个区间,从理论上说在这个区间内可取任一实数3.5、无理数等,因而称这随机变量是连续型随机变量
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








