数据结构17————树,森林转化为二叉树(孩子兄弟表示法)

数据结构17————树,森林转化为二叉树(孩子兄弟表示法)

一. 内容

1. 树转换二叉树
2. 森林转换为二叉树
3. 二叉树转森林和树
4. 森林和树的遍历
5. 二叉森林树的应用

二.树转为二叉树

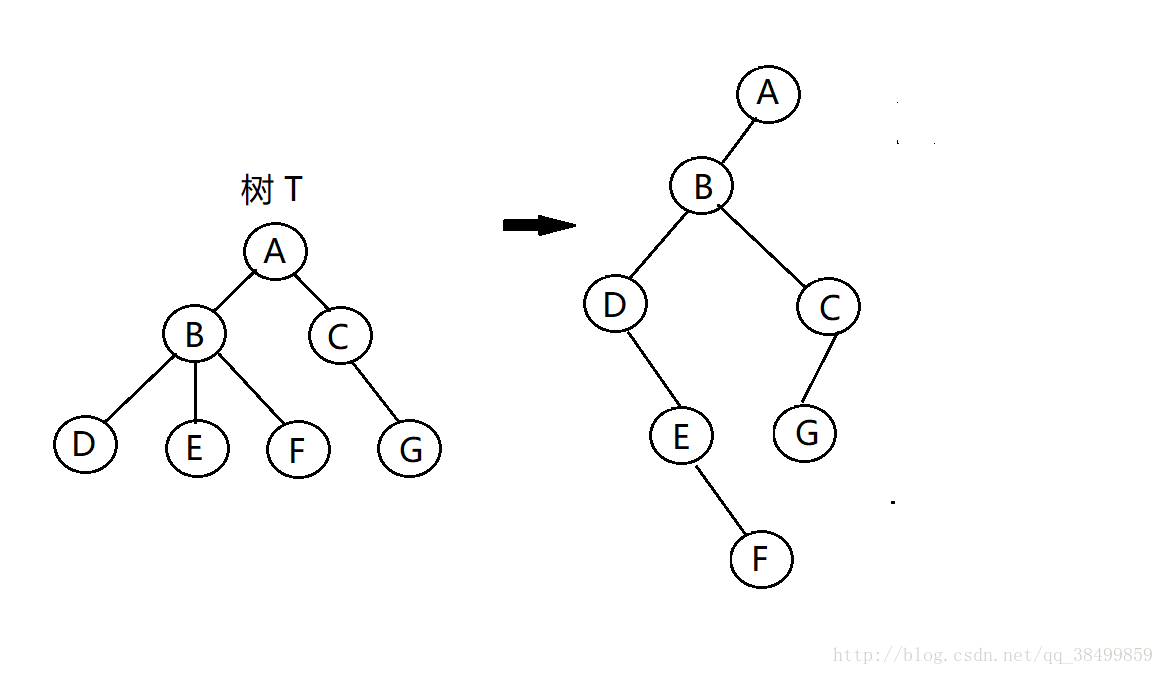
1.思路

整体思路就是我前面的一篇博客提到的树的孩子兄弟法。
就是对于一个节点:

• 左指针指向它的第一个孩子
• 右指针指向它的右兄弟

2.例子

三.森林转二叉树

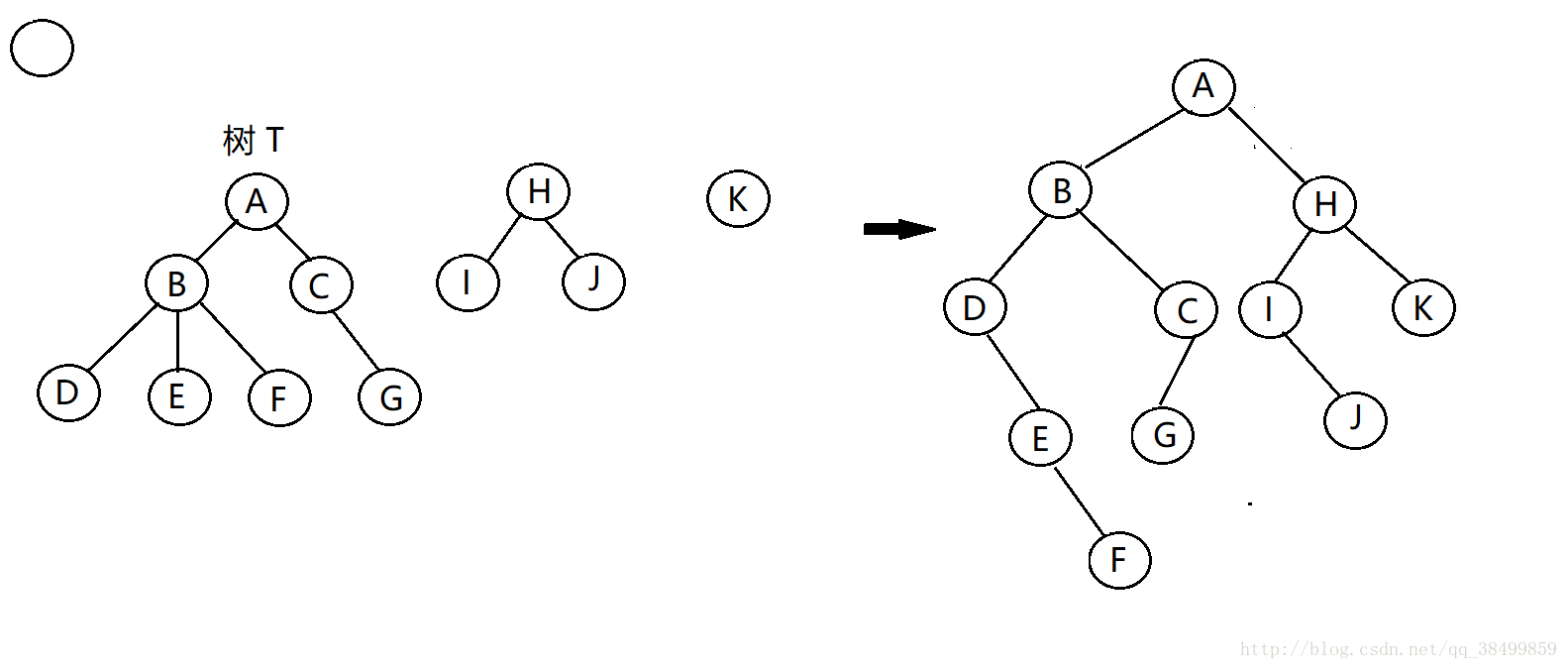
1.思路

和树的兄弟节点很想，只是把树的左边的树也当做根节点的兄弟
就是对于任一个节点：

• 左指针指向它的第一个孩子
• 右指针指向它的兄弟/旁边的树

2.例子

四.二叉树转换为树或森林

二叉树转树和森林就是上面过程的逆过程。即
对于任意一个节点:

• 左子树转换为它的子树
• 如果是根节点,右子树转换为另一颗树,如果不是，右子树转换为该节点的兄弟

五.树和森林的遍历

1.树的遍历

a.先根遍历

• 即先访问树的根节点，然后依次访问根的每颗子树。
• 以前面的那个树T为例，它的先根遍历为ABDEFCG
• 很显然树的先根遍历 = 转换后二叉树的先序遍历

b.后根遍历

• 即先访问树的每颗子树，在访问根节点
• 以前面那个树为例,它的先根遍历为DEFBCGA
• 很显然树的后跟遍历 = 转换后二叉树的中序遍历

2.森林的遍历

a.先序遍历

• 即先访问第一个树的根节点，然后依次遍历这颗树的子树,然后依次访问剩下的树
• 以前面的森林为例，它的先序遍历序列为ABDEFCGHIJK
• 很显然森林的先序遍历 = 转换后二叉树的先序遍历

b.后序遍历

• 即先访问第一棵树的各个子树,然后访问根节点，然后依次访问剩下的树
• 以前面那个森林为例，它的后序遍历序列为DEFBGCAIJHK
• 很显然森林的后序遍历 = 转换后二叉树的中序遍历

六.二叉森林的应用

1.求树叶子节点个数。

具体要求：编写算法，在以孩子兄弟二叉链表存储的树中,求树(森林)叶子节点个数。
思路: 使用二叉树的遍历算法，遍历所有节点,如果左子树为空，则说明在这个树中，该节点为叶子节点。

int Statistics(BiTree	root){
	static int count;
	if(root==NULL)
		return ;
	if(root->lChild==NULL)
		count++;
		
	Statistics(root->lChild);
	Statistics(root->rChild);

	return count;
} 

2.求树的深度。

具体要求：编写算法,在以孩子兄弟二叉链表存储的树中,求树(或森林)的深度。
思路:树的深度=左子树深度+1和右子树深度中大者。

int Depth(BiTree root){
	int hchild,hsibling;
	
 	if(root==NULL)
		return 0;
		
	hchild=Depth(root->lChild);
	hsibling =Depth(root->rChild);
	
	if(hchild+1>hsibling){
		return hchild+1;
	}else{
		return hsibling;
	}
}

text14中