【运筹学】

最新推荐文章于 2024-08-08 14:03:17 发布

yangbocsu

最新推荐文章于 2024-08-08 14:03:17 发布

阅读量2.3k

点赞数

分类专栏： 00 CSU学习生活

本文为博主原创文章，未经博主允许不得转载。

本文链接：https://blog.csdn.net/qq_38689263/article/details/109082371

版权

00 CSU学习生活专栏收录该内容

205 篇文章

订阅专栏

运筹学主要解决最优化问题，通过数学建模和约束条件分析来寻找函数的最大值和最小值。在面对强约束时，使用拉格拉日乘数法；弱约束条件下，则应用KKT定理。高等数学基础中，多元函数的最值问题涉及到黑塞矩阵。博客深入探讨了这些概念及其在实际问题中的应用。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

【运筹学】

第1讲导学与绪论

线性代数就是通过一系列的手段“折腾”方程组，提取系统信息。

总结：《运筹学》要解决的是一般视觉下的最优化问题，就是寻找一般函数的最大值和最小值问题；怎么操作？

①抽象实际问题，数学建模；

②求解这个数学模型；然后怎么解呢？

③首先研究这个函数，看它的约束条件是强约束条件还是弱约束条件；

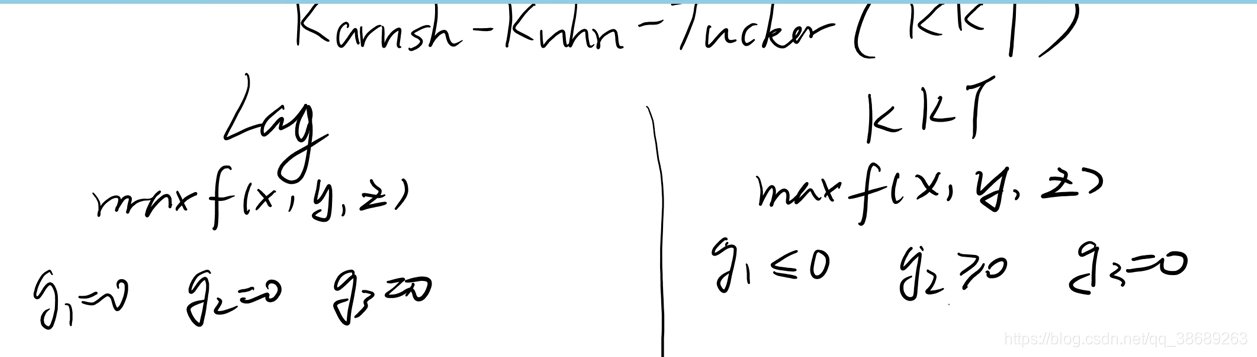
④如果受到的是强约束条件，我们可以用拉格拉日乘数法；如果是弱约束条件，我们可以用KKT定理；我们还要注意我们所求解的实际问题的自然定义域和真实定义域

---------------------------------------------------------------------------------------------------------------------------------------------------------

第2讲高等数学基础

一、最值与极值

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------

多元函数真正极值问题：

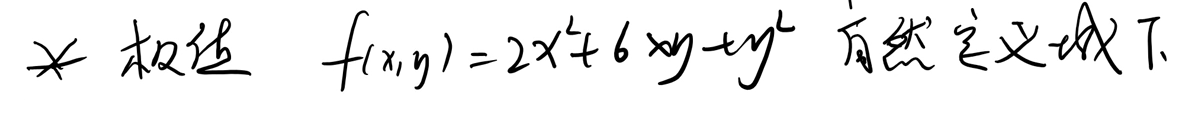
黑塞矩阵（Hessian Matrix）：

---------------------------------------------------------------------------------------------------------------------------------------------------------------------

-------------------------------------------------------------------------------------------------------------------------------------------------------------------------