第7讲 线性规划与单纯形法(标准型、基、基解、基可行解、可行基)
线性规划问题的标准形式
将约束条件由弱约束变为强约束,将不等式组变为了方程组,降低了求解的难度。
对于一般的线性规划问题,容易得到:
目标函数 max ( min ) z = c 1 x 1 + c 2 x 2 + ⋯ + c n x n \quad \max (\min ) z=c_{1} x_{1}+c_{2} x_{2}+\cdots+c_{n} x_{n} max(min)z=c1x1+c2x2+⋯+cnxn
约束条件 { a 11 x 1 + a 12 x 2 + ⋯ + a 1 n x n ⩽ ( = , ⩾ ) b 1 a 21 x 1 + a 22 x 2 + ⋯ + a 2 n x n ⩽ ( = , ⩾ ) b 2 ⋮ a m 1 x 1 + a m 2 x 2 + ⋯ + a m n x n ⩽ ( = , ⩾ ) b m x 1 , x 2 , ⋯ , x n ⩾ 0 } \left\{\begin{array}{c}a_{11} x_{1}+a_{12} x_{2}+\cdots+a_{1 n} x_{n} \leqslant(=, \geqslant) b_{1} \\ a_{21} x_{1}+a_{22} x_{2}+\cdots+a_{2 n} x_{n} \leqslant(=, \geqslant) b_{2} \\ \vdots \\ a_{m 1} x_{1}+a_{m 2} x_{2}+\cdots+a_{m n} x_{n} \leqslant(=, \geqslant) b_{m} \\ x_{1}, \quad x_{2}, \cdots, \quad x_{n} \geqslant 0\end{array}\right\} ⎩⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎧a11x1+a12x2+⋯+a1nxn⩽(=,⩾)b1a21x1+a22x2+⋯+a2nxn⩽(=,⩾)b2⋮am1x1+am2x2+⋯+amnxn⩽(=,⩾)bmx1,x2,⋯,xn⩾0⎭⎪⎪⎪⎪⎪⎬⎪⎪⎪⎪⎪⎫
通过恒等变形将一般形式化为标准形式,以方便之后的求解。
- 目标函数需要化为 m a x max max。若原本的目标函数是 m i n min min,则令 z ′ = − z z^{'}=-z z′=−z,然后求 m a x z ′ max z^{'} maxz′。
- b i b_i bi需要化为 > 0 >0 >0。如果 b i < 0 b_i<0 bi<0则不等式两边同时添负号。如果 b i = 0 b_i=0 bi=0则表示出现了退化,一般不会遇到。
- 约束条件需要化为 = = =。若原本的约束条件是 ≤ \leq ≤,则约束条件变为原本的约束条件减去一个新的非负变量(松弛变量)。若原本的约束条件是 ≥ \geq ≥,则约束条件变为原本的约束条件加上一个新的非负变量(剩余变量)。(这一步的目的是将弱约束条件变为强约束条件,便于求解方程,代价是引入了额外的变量,提高了方程的维数。)
- 变量需要化为 ≥ 0 \ge0 ≥0。若原本的变量是 = 0 =0 =0,则直接改为 ≥ 0 \ge0 ≥0,但实际上这种情况并不会出现,因为如果变量 = 0 =0 =0,那么改变量就不会在目标函数和约束条件中出现。若原本的变量是 ≤ 0 \le0 ≤0,则令 x i ′ = − x i x_i^{'}=-x_i xi′=−xi,并令 x i ′ ≥ 0 x_i^{'}\ge0 xi′≥0,同时目标函数和约束条件中进行替换。若原本的变量没有约束( ∈ \in ∈R),则令 x i = x i ′ − x i ′ ′ x_i=x_i^{'}-x_i^{''} xi=xi′−xi′′,并令 x i ′ ≥ 0 x i ′ ′ ≥ 0 x_i^{'}\ge0\ x_i^{''}\ge0 xi′≥0 xi′′≥0,同时目标函数和约束条件中进行替换。
- 规范书写目标函数。在形式上调整目标函数,把新引入的变量写回目标函数中。虽然其价值系数为0,但是也要写出来。
线性规划的解的讨论
首先将线性规划问题的标准形式写成矩阵形式。
A = ( a 11 a 12 ⋯ a 1 n ⋮ ⋮ ⋮ a m 1 a m 2 ⋯ a m n ) = ( P 1 , P 2 , ⋯ , P n ) ; O = [ 0 0 ⋮ 0 ] \boldsymbol{A}=\left(\begin{array}{cccc}a_{11} & a_{12} & \cdots & a_{1 n} \\ \vdots & \vdots & & \vdots \\ a_{m 1} & a_{m 2} & \cdots & a_{m n}\end{array}\right)=\left(\boldsymbol{P}_{1}, \boldsymbol{P}_{2}, \cdots, \boldsymbol{P}_{n}\right) ; \quad \boldsymbol{O}=\left[\begin{array}{c}0 \\ 0 \\ \vdots \\ 0\end{array}\right] A=⎝⎜⎛a11⋮am1a12⋮am2⋯⋯a1n⋮amn⎠⎟⎞=(P1,P2,⋯,Pn);O=⎣⎢⎢⎢⎡00⋮0⎦⎥⎥⎥⎤
X = [ x 1 x 2 ⋮ x n ] ; b = [ b 1 b 2 ⋮ b m ] \boldsymbol{X}=\left[\begin{array}{c}x_{1} \\ x_{2} \\ \vdots \\ x_{n}\end{array}\right] ; \quad \boldsymbol{b}=\left[\begin{array}{c}b_{1} \\ b_{2} \\ \vdots \\ b_{m}\end{array}\right] X=⎣⎢⎢⎢⎡x1x2⋮xn⎦⎥⎥⎥⎤;b=⎣⎢⎢⎢⎡b1b2⋮bm⎦⎥⎥⎥⎤ ; C = ( c 1 , c 2 , ⋯ , c n ) ; \quad \boldsymbol{C}=\left(c_{1}, c_{2}, \cdots, c_{n}\right) ;C=(c1,c2,⋯,cn)
线性规划问题可以用矩阵描述为:
max
z
=
C
X
\max z=\boldsymbol{C}\boldsymbol{X}
maxz=CX
A
X
=
b
\boldsymbol{A} \boldsymbol{X}=\boldsymbol{b}
AX=b
X
⩾
0
\boldsymbol{X} \geqslant 0
X⩾0
可行解
满足约束条件式 A X = b \boldsymbol{A} \boldsymbol{X}=\boldsymbol{b} AX=b、 X ⩾ 0 \boldsymbol{X} \geqslant 0 X⩾0的解称为线性规划的可行解,其中使目标函数达到最大值的可行解称为最优解。
基
设 A A A是约束方程组的 m × n ( m < n ) m \times n(m<n) m×n(m<n)维系数矩阵,其秩为 m m m。 B B B是矩阵 A A A中 m × m m \times m m×m阶子矩阵,其中 B B B的列向量都是线性独立的,且 ∣ B ∣ = 0 |B|=0 ∣B∣=0,则称矩阵 B B B是线性规划问题的一个基。
B B B中的 P i P_i Pi称为基向量,不在 B B B中的 P i P_i Pi称为非基向量。假设前 m m m个变量的系数列向量是线性独立的,用这些向量构成矩阵 B B B,那么约束条件 A X = b \boldsymbol{A} \boldsymbol{X}=\boldsymbol{b} AX=b可以写成:
( a 11 a 21 ⋮ a m 1 ) x 1 + ( a 12 a 22 ⋮ a m 2 ) x 2 + ⋯ + ( a 1 m a 2 m ⋮ a m m ) x m = ( b 1 b 2 ⋮ b m ) − ( a 1 , m + 1 a 2 , m + 1 ⋮ a m , m + 1 ) x m + 1 − ⋯ − ( a 1 n a 2 n ⋮ a m n ) x n \begin{aligned} &\left(\begin{array}{c}a_{11} \\ a_{21} \\ \vdots \\ a_{m 1}\end{array}\right) x_{1}+\left(\begin{array}{c}a_{12} \\ a_{22} \\ \vdots \\ a_{m 2}\end{array}\right) x_{2}+\cdots+\left(\begin{array}{c}a_{1 m} \\ a_{2 m} \\ \vdots \\ a_{m m}\end{array}\right) x_{m}=\left(\begin{array}{c}b_{1} \\ b_{2} \\ \vdots \\ b_{m}\end{array}\right)-\left(\begin{array}{c}a_{1, m+1} \\ a_{2, m+1} \\ \vdots \\ a_{m, m+1}\end{array}\right) x_{m+1}-\cdots-\left(\begin{array}{c}a_{1 n} \\ a_{2 n} \\ \vdots \\ a_{m n}\end{array}\right) x_{n} \end{aligned} ⎝⎜⎜⎜⎛a11a21⋮am1⎠⎟⎟⎟⎞x1+⎝⎜⎜⎜⎛a12a22⋮am2⎠⎟⎟⎟⎞x2+⋯+⎝⎜⎜⎜⎛a1ma2m⋮amm⎠⎟⎟⎟⎞xm=⎝⎜⎜⎜⎛b1b2⋮bm⎠⎟⎟⎟⎞−⎝⎜⎜⎜⎛a1,m+1a2,m+1⋮am,m+1⎠⎟⎟⎟⎞xm+1−⋯−⎝⎜⎜⎜⎛a1na2n⋮amn⎠⎟⎟⎟⎞xn
现若令上式的非基变量 x m + 1 = x m + 2 = ⋯ = x n = 0 x_{m+1}=x_{m+2}=\cdots=x_{n}=0 xm+1=xm+2=⋯=xn=0,这时变量的个数等于线性方程的个 数。用高斯消去法,可以求出一个解 X = ( x 1 , x 2 , ⋯ , x m , 0 , ⋯ , 0 ) T \boldsymbol{X}=\left(x_{1}, x_{2}, \cdots, x_{m}, 0, \cdots, 0\right)^{\mathrm{T}} X=(x1,x2,⋯,xm,0,⋯,0)T,将这个解称为基解(注意基解是 n n n维的,而不是 m m m维的。)。由此可见有一个基就可以求出一个基解。
基可行解
满足非负条件约束 X ⩾ 0 \boldsymbol{X} \geqslant 0 X⩾0的基解称为基可行解。
可行基
可行解对应的基称为可行基。
基解和基可行解的几何意义
基解的几何意义是:强约束方程的交点。
基可行解的几何意义是:强约束方程的交点(基解),并且是可行域中的点。(换言之即可行域的顶点。)
此处读者可以自行举一个例子,并在图中画出来,然后在图中找出可行解、基可行解、基解和非可行解分别是哪一部分。
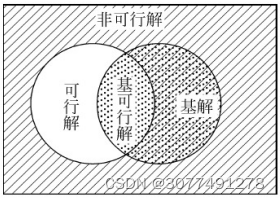
基解、可行解和基可行解的关系
上述几种解之间的包含关系可以用下图表示:
由基可行解求最优解
综上所述,找出所有的基,然后得到所有的基可行解,其对应的函数值中最大的就是最优解。当然,这种方法属于枚举法,而在之后的学习中可以通过一定的顺序比较基可行解对应的函数值,也就是单纯形法,这样就可以用比较少的对比次数找出最优解。
总结
为了方便寻找可行解,需要先把线性规划问题化为标准型,主要需要对目标函数、自由项、弱约束条件、自变量进行处理。
对于约束方程组,可以用线性代数的思想进行处理,找到系数矩阵的基,令非基变量为0,可以得到一个由基变量构成的方程组,可以解出唯一解,然后据此得到基解。一个系数矩阵可能有若干个基,每一个基都可以得到一个基解,若基解满足 X ⩾ 0 \boldsymbol{X} \geqslant 0 X⩾0,则该基解还是基可行解,可行解对应的基称为可行基。基可行解对应的函数值中最大的就是最优解。
基可行解的几何意义是可行域的顶点。
可行解和基解的交集为基可行解。
在之后的学习中可以通过一定的顺序比较基可行解对应的函数值,这样就可以用比较少的对比次数找出最优解。





















 3万+
3万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








