【图论】Laplacian matrix

原文阅读

Laplacian matrix

Laplacian matrix是图论数学领域的一个概念，又名graph Laplacian, admittance matrix, Kirchhoff matrix或discrete Laplacian，是一个图的矩阵表示。

Definition

Laplacian matrix for simple graphs

给定一个有$n$个节点的简单图$G$，它的Laplacian矩阵${\mathbf{L}}_{\mathbf{n}\times \mathbf{n}}$可以定义为
$$\mathbf{L}=\mathbf{D}-\mathbf{A},$$
其中，$\mathbf{D}$是一个degree矩阵，$\mathbf{A}$是一个adjacency矩阵。对于simple图，$\mathbf{A}$是一个对角线上元素为0的二值矩阵。

对于directed图，indegree或outdegree都可能用到，完全取决于应用。

$\mathbf{L}$元素为
$${\mathbf{L}}_{i,j}:=\{\begin{array}{rl}\mathrm{deg}(v_i)& \text{if}i=j\\ -1& \text{if}i\ne j\text{and}{v}_i\sim v_j\\ 0& \text{otherwise}\end{array},$$
其中，$\sim$表示$v_i$与$v_j$邻接。

Symmetric normalized Laplacian

对称归一化Laplacian矩阵被定义为
$${\mathbf{L}}^{\text{sys}}:={\mathbf{D}}^{-\frac{1}{2}}\mathbf{L}{\mathbf{D}}^{-\frac{1}{2}}=\mathbf{I}-{\mathbf{D}}^{-\frac{1}{2}}\mathbf{A}{\mathbf{D}}^{-\frac{1}{2}}.$$
${\mathbf{L}}^{\text{sys}}$元素为
$${\mathbf{L}}_{i,j}^{\text{sys}}:=\{\begin{array}{rl}1& \text{if}i=j\text{and}\mathrm{deg}(v_i)\ne 0\\ -\frac{1}{\sqrt{\mathrm{deg}(v_i)\mathrm{deg}(v_j)}}& \text{if}i\ne j\text{and}{v}_i\sim v_j\\ 0& \text{otherwise}\end{array}.$$

Random walk normalized Laplacian

随机游走归一化Laplacian矩阵定义为
$${\mathbf{L}}^{\text{rw}}:={\mathbf{D}}^{-1}\mathbf{L}=\mathbf{I}-{\mathbf{D}}^{-1}\mathbf{A}.$$
${\mathbf{r}\mathbf{w}}^{\text{sys}}$元素为
$${\mathbf{L}}_{i,j}^{\text{rw}}:=\{\begin{array}{rl}1& \text{if}i=j\text{and}\mathrm{deg}(v_i)\ne 0\\ -\frac{1}{\sqrt{\mathrm{deg}(v_i)}}& \text{if}i\ne j\text{and}{v}_i\sim v_j\\ 0& \text{otherwise}\end{array}.$$

Generalized Laplacian

广义Laplacian被定义为
$${\mathbf{Q}}_{i,j}^{\text{rw}}:=\{\begin{array}{rl}<0& \text{if}i=j\text{and}\mathrm{deg}(v_i)\ne 0\\ =0& \text{if}i\ne j\text{and}{v}_i\sim v_j\\ \text{any number}& \text{otherwise}\end{array}.$$

Notice the ordinary Laplacian is a generalized Laplacian.

Example

Labelled graph

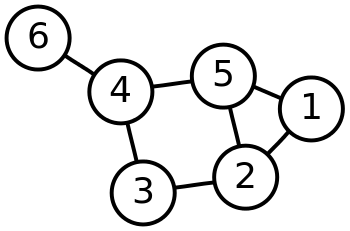
Degree matrix

$$\left(\begin{array}{cccccc}2& 0& 0& 0& 0& 0\\ 0& 3& 0& 0& 0& 0\\ 0& 0& 2& 0& 0& 0\\ 0& 0& 0& 3& 0& 0\\ 0& 0& 0& 0& 3& 0\\ 0& 0& 0& 0& 0& 1\end{array}\right)$$

Adjacency matrix

$$\left(\begin{array}{cccccc}0& 1& 0& 0& 1& 0\\ 1& 0& 1& 0& 1& 0\\ 0& 1& 0& 1& 0& 0\\ 0& 0& 1& 0& 1& 1\\ 1& 1& 0& 1& 3& 0\\ 0& 0& 0& 1& 0& 0\end{array}\right)$$

Laplacian matrix

$$\left(\begin{array}{cccccc}2& -1& 0& 0& -1& 0\\ -1& 3& -1& 0& -1& 0\\ 0& -1& 2& -1& 0& 0\\ 0& 0& -1& 3& -1& -1\\ -1& -1& 0& -1& 3& 0\\ 0& 0& 0& -1& 0& 1\end{array}\right)$$

Properties

对于无向图$G$，其Laplacian矩阵为$\mathbf{L}$，$\mathbf{L}$特征值为${\lambda }_0\le {\lambda }_1\le \cdots {\lambda }_{n-1}$，则有：

• $\mathbf{L}$是对称的；

• $\mathbf{L}$是正定的（${\lambda }_i\ge 0,\forall i$）；

• ${\sum }_{i=0}^{n-1}{\mathbf{L}}_{i,j}={\sum }_{j=0}^{n-1}{\mathbf{L}}_{i,j}=1$；

• ${\lambda }_0=0,{v\text{v}v}_0=(1,1,\cdots ,1)$；

• Laplacian是$n$维向量空间上的函数算子$f:V\to \mathbb{R}$；

  $$\mathbf{L}f(v_i)=\sum _{v_j\sim v_i}{w}_{i,j}(f(v_i)-f(v_j)$$

• 二次型：

  $$f^T\mathbf{L}f(v_i)=\frac{1}{2}\sum _{e_{i,j}}{w}_{i,j}(f(v_i)-f(v_j)$$

• ……

Incidence matrix

Incidence matrix刻画了两类对象之间的关系，在graph theory中有广泛的应用。

Undirected and directed graphs

对于图$G=(V,E)$，$n$个顶点，$m$条边（$|V| \times |E| = m \times n $），有两种incidence矩阵：

• Unoriented incidence matrix

  • 对于无向图

  $${\mathbf{B}}_{i,j}:=\{\begin{array}{rl}1& v_i-e_j\\ 0& \text{otherwise}\end{array}.$$

  • 对于有向图

  $${\mathbf{B}}_{i,j}:=\{\begin{array}{rl}1& v_i\to e_j\\ 1& v_i\leftarrow e_j\\ 0& \text{otherwise}\end{array}.$$

• Oriented incidence matrix

  • 对于无向图：无向图的有向关联矩阵是图的任何方向的关联矩阵。

  • 对于有向图

  $${\mathbf{B}}_{i,j}:=\{\begin{array}{rl}1& v_i\to e_j\\ -1& v_i\leftarrow e_j\\ 0& \text{otherwise}\end{array}.$$

Boundary operator

图的boundary operator定义为：
$$\vartheta :E(G)\to V(G)$$
而图的co-boundary operator定义为：
$$\pi :V(G)\to E(G)$$

Discrete differential operator

Incidence矩阵是离散的微分算子。

• $f\to \mathbf{B}f$是一个co-boundary mapping；

• 特别地，$(\mathbf{B}f)(e_{i,j})f(v_j)-f(v_i)$

• Example：
  $$\left(\begin{array}{c}f(2)-f(1)\\ f(1)-f(3)\\ f(3)-f(2)\\ f(4)-f(2)\end{array}\right)=\left(\begin{array}{cccc}-1& 1& 0& 0\\ 1& 0& -1& 0\\ 0& -1& 1& 0\\ 0& -1& 0& 1\end{array}\right)\left(\begin{array}{c}f(1)\\ f(2)\\ f(3)\\ f(4)\end{array}\right)$$

Laplacian & incidence

$$\mathbf{L}=\mathbf{B}{\mathbf{B}}^T$$