Leetcode-1091. 二进制矩阵中的最短路径（Java）

给你一个 n x n 的二进制矩阵 grid 中，返回矩阵中最短 畅通路径 的长度。如果不存在这样的路径，返回 -1 。

二进制矩阵中的 畅通路径 是一条从 左上角 单元格（即，(0, 0)）到 右下角 单元格（即，(n - 1, n - 1)）的路径，该路径同时满足下述要求：

路径途经的所有单元格都的值都是 0 。
路径中所有相邻的单元格应当在 8 个方向之一 上连通（即，相邻两单元之间彼此不同且共享一条边或者一个角）。
畅通路径的长度 是该路径途经的单元格总数。

示例 1：
 

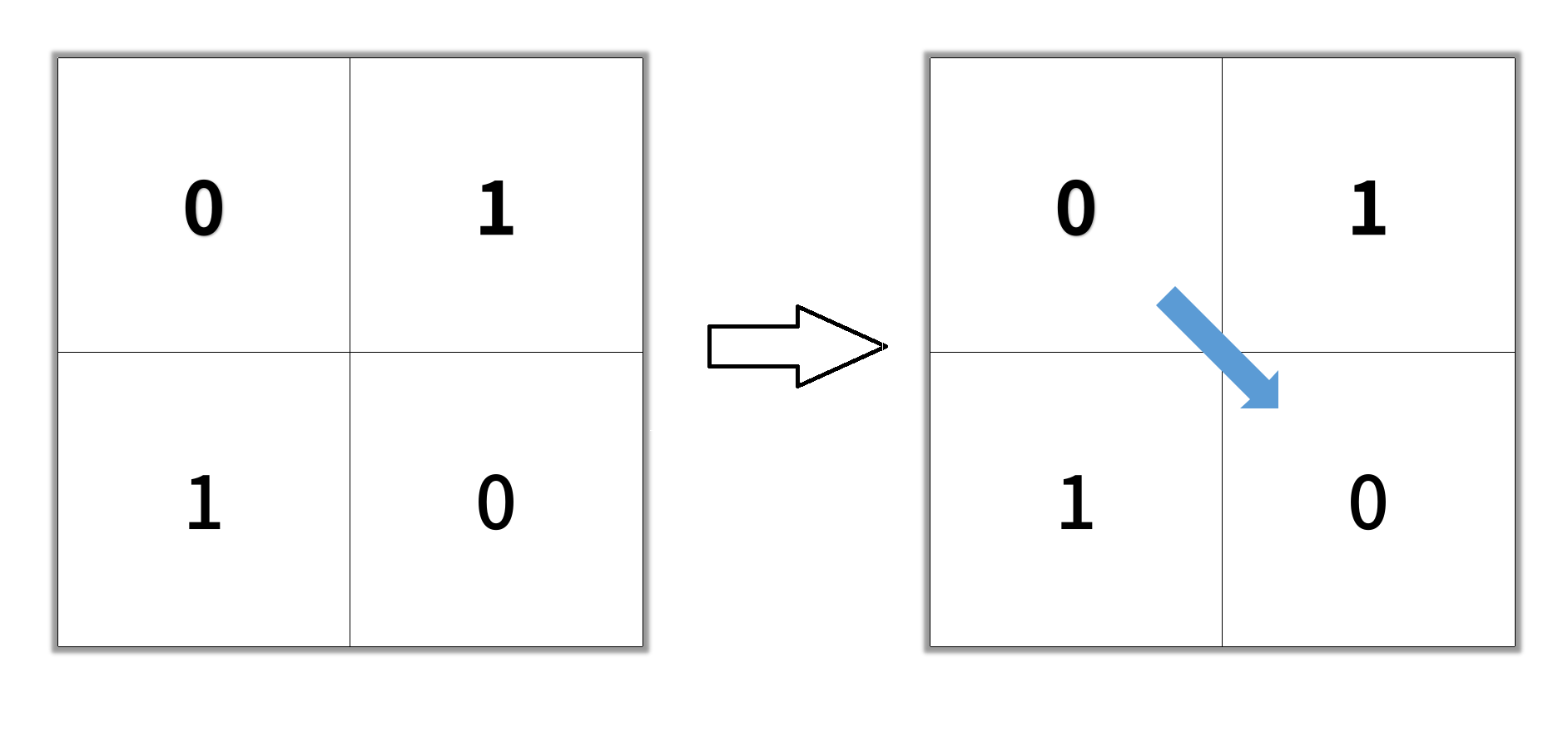
输入：grid = [[0,1],[1,0]]
输出：2

示例 2：

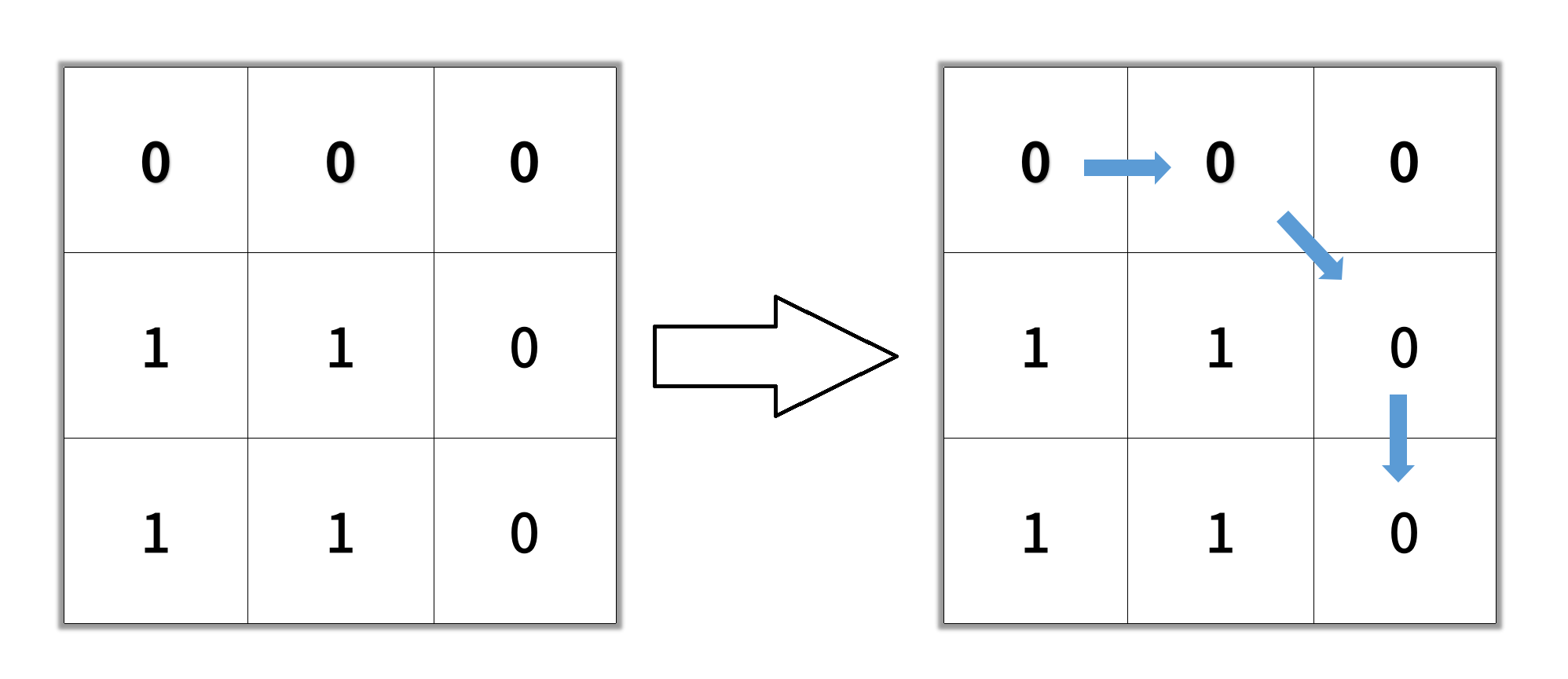
输入：grid = [[0,0,0],[1,1,0],[1,1,0]]
输出：4
示例 3：

输入：grid = [[1,0,0],[1,1,0],[1,1,0]]
输出：-1
 

提示：

n == grid.length
n == grid[i].length
1 <= n <= 100
grid[i][j] 为 0 或 1

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/shortest-path-in-binary-matrix

class Solution {
    public int shortestPathBinaryMatrix(int[][] grid) 
    {
        if(grid==null) return -1;

        int row = grid.length;
        int col = grid[0].length;
        boolean[][] visited = new boolean[row][col];
        int count=0;

        int[][] dir={{0,-1},{-1,-1},{-1,0},{-1,1},{0,1},{1,1},{1,0},{1,-1}};

        Queue<int[]> queue = new LinkedList<>();
        
        if(grid[0][0] == 0) 
        {
            queue.offer(new int[]{0,0});
            visited[0][0] = true;
        }

        while(!queue.isEmpty())
        {
            int size = queue.size();
            for(int i=0;i<size;i++)
            {
                int[] point = queue.poll();
                if(point[0]==row-1 && point[1]==col-1) 
                {
                    visited[point[0]][point[1]]=true;
                    return count+1;
                }
                for(int j=0;j<8;j++)
                {
                    int x = point[0] + dir[j][0];
                    int y = point[1] + dir[j][1];

                    if(x < 0  || x >= row || y < 0 || y >= col 
                        || visited[x][y] || grid[x][y] == 1)                 
                    {
                        continue;
                    }
                    else
                    {
                        queue.offer(new int[]{x,y});
                        visited[x][y] = true;
                    }         
                }
            }
            count++;
        }
    
        return -1;
    }
}