中缀表达式与后缀表达式的转换及后缀表达式的计算

一.后缀表达式的计算
后缀表达式：
指的是不包含括号，运算符放在两个运算对象的后面，所有的计算按运算符出现的顺序，严格从左向右进行。（不再考虑运算符的优先规则）。

中缀表达式：
也就是我们日常最容易见到的表达式，从左至右考虑运算符的优先原则。

首先，我们以电脑的思维计算后缀表达式，这里必须用到栈的知识，栈通俗来讲就像一个桶，它里边存放的东西必须满足先进后出的原则。

我们以表达式1 2 4 8 2 - 7 4 - / * + *为例讲解。

         **后缀表达式用栈计算的原则就是遇到数字就入栈，遇到运算符就把栈顶两数字计算，再把计算结果入栈，这样反复直到栈空。**

具体过程如下：
第一步：1，2，4，8，2按顺序进栈，遇减号，栈顶2做减数，8做被减数，相减得6入栈

第二步：7，4按顺序进栈，遇减号 ，栈顶4做减数，7做被减数，相减得3入栈

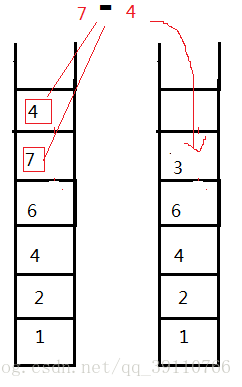
第三步： 遇除号，栈顶3作为除数，6作为被除数，运算得2入栈

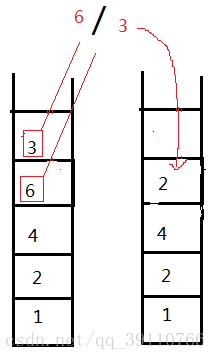
第四步：遇乘号，栈顶元素2，4相乘得8入栈

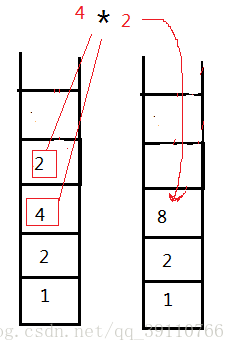
第五步：遇加号，栈顶元素8，2相乘得10入栈

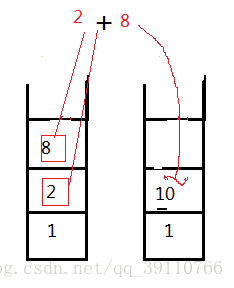
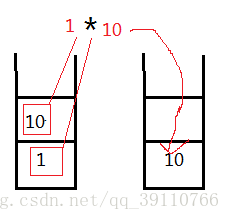
第六步：遇乘号，栈顶元素10，1相乘得10入栈

第七步：输出栈底元素10，即该后缀表达式结果为10

以上就是后缀表达式求解的思想
二.中缀表达式与后缀表达式的转换

对于中缀表达式与后缀表达式的转换有一个简便方法，就是先用括号按运算符优先级把中缀表达式一层一层括起来，每遇到一个括号，就把括号里面的运算符放在本层括号外边,直到把所有的运算符都都放在括号外边，再把括号去掉，得到的表达式就是对应的后缀表达式。

例如：x=a+b*(c-d)/e

        x = a + ( b * ( c - d) ) / e

        x = a + （ (b * ( c - d ) ) / e )

        x = (  (a + ( ( b * ( c - d ) ) / e ) )

       x = (  (a + ( b * (c d )- ) ) / e ) )

       x = ( (  a  + ( b (c d)- ) * ) / e) )

         x = ( ( a  ( b (c d) - ) * ) e ) / )+

       ( x  ( ( a ( b) c d ) - ) * ) e ) / ) + ) =

最后把括号去掉：x a b c d - * e / + =  

其实按这个方法真的是既简单又不容易错，希望可以帮助到大家，如果有什么错误，也欢迎大家指出，谢谢。