矩阵论-线性空间与线性映射

WALL-SQ

已于 2022-01-31 22:54:08 修改

阅读量4.3k

点赞数 7

分类专栏：矩阵论文章标签：矩阵

于 2022-01-08 18:17:15 首次发布

本文链接：https://blog.csdn.net/qq_39304630/article/details/122378723

版权

矩阵论专栏收录该内容

1 篇文章 0 订阅

订阅专栏

0.导言

矩阵论真难啊QaQ，做个笔记，以哈工大严质彬老师的讲解为例，很推荐，讲的非常不错~

传送门：矩阵论_哔哩哔哩_bilibili

1.线性空间与线性映射

给定非空集合V和域F，若存在映射：

$V\ X\ F->V \\(V_1,F_1)|->\zeta (V_1,F_1)$

则称 $\sigma$ 为V上的加法；

若存在映射：

$V\ X\ V->V \\(V_1,V_2)|->\sigma(V_1,V_2)$

则称 $\zeta$ 为V上的数乘。

1)注1：

域：是一个系统，其中定义了两种运算-加法和乘法，若这两个运算在这个系统上满足一些比较好的性质，是的+的逆运算-可以在该系统上能进行，*的逆运算/也可以在该系统上进行，则称该运算系统为域。换句话说，域是一个满足+、-、*、/四种运算的系统。

举例：

1.所有非负整数集合 $Z_+$ ，可以满足+和*，即两个非负整数经过+和*之后还是一个非负整数，但是-可能会产生负数，/可能会产生分数，因此这就不能称之为一个域。

2.所有整数集合Z，可以满足+、-和*，但是满足不了/。

3.有理数集合Q，我们知道任何两个整数的比就是有理数，因此在有理数集合上/也封闭了。该运算系统就是一个域（值得0作为分母时除法无意义，但不在我们的考虑范围内）。

4.实数域R

5.复数域C

上面例子告诉我们，实际上域的要求就是运算封闭，即运算后的结果仍然在这个集合规定的范围内。

2)注2：

上述的X表示的是集合之间的笛卡尔积，而不是乘法。对笛卡尔积的定义如下：

我们存在两个集合 $S_1,S_2$ ，则

$S_1\ X\ S_2=\{[s_1\ s_2]^T,s_1\epsilon S_1,s_2\epsilon S_2\}$

笛卡尔积是一种带顺序的运算，即 $S_1\ X\ S_2!=S_2\ X\ S_1$ 。

3)映射：

映射就是代表着我们可以讲某一集合上的元素通过某一种变化变成另一个集合上的元素，可能存在维度变化。即原始的n维向量经过映射变为了m维向量。因此我们定义映射如下：

$f:A->B$

另一种映射记号：

$f: a\ |->\ b$

->表示的是集合之间的映射，而|->是针对单个元素来说的映射。

举个例子：假设我们存在映射 f=sin(.)，那么

$f:(-\infty,+\infty)->(-1,1)$

$f:1\ |->\ sin1$

现在我们回过头来看我们上面的定义

给定非空集合V和域F，若存在映射：

$V\ X\ V->V \\(V_1,V_2)|->\sigma(V_1,V_2)$

则称 $\sigma$ 为V上的加法。

也就是说我们从V中集合取两个元素，经过一种映射后，得到另一个仍旧属于V的元素，我们称这个运算为集合V上的加法。

若存在映射：

$V\ X\ V->V \\(V_1,V_2)|->\sigma(V_1,V_2)$

则称 $\zeta$ 为V上的数乘。

也即是所我们从集合V中取一个元素，从数域F中取一个元素，经映射后得到一个仍旧属于V的元素，就称这个运算为集合V上的数乘。

这里的概念一定要理解并且接受，因为整个矩阵论会颠覆我们对传统运算的认知，后面我们会大批重新定义我们以前见过的一些运算；所有的运算都是人为规定的，因此我们重新在不同的域上定义运算的具体方式也未尝不可呀~

4)线性空间

当我们上述的加法和数乘满足通常的运算规则，则称V关于加法和数乘法构成F上的线性空间。有时候线性空间也被称之为向量空间，V中的元素有时也称为向量。

通常的运算规则：以下使用+和*替代符号 $\sigma,\zeta$

关于加法的部分

1)加法交换律 $V_1+V_2=V_2+V_1$

2)加法结合律 $(V_1+V_2)+V_3=V_1+(V_2+V_3)$

3)有零元存在e∈V，满足 $e+v=v$

4)有负元对任意v∈V，存在a∈V，使得 $v+a=e$ ，记 a = -v

关于数乘法的部分

5)分配率A $(V_1+V_2)*k=V_1*k+V_2*k$

6)分配率B $V*(k_1+k_2)=V*k_1+V*k_2$ ，注意等式两边的加法是不一样的，左边的加法是数域F中的加法，右边的是V集合中定义的加法

7)与数域F中元素的乘法关系 $V*(kl)=(V*k)*l$ ，注意等式两边乘法也不同，左边是数域F中的乘法，右边是V集合中的元素与数域中的元素的数乘

8)与数域F中1的关系 $V*1=V$

注：V实际上是一个集合，而我们之所以将其称之为空间是为了通过以几何的方式来理解它。

严老师课外话题：数乘法为什么写在右边而不是在左边

以列向量的数乘法为例，将数字写在右边就可以将数乘法理解为矩阵乘法。

也就是说，对列向量来说，数乘法的数应写在右边，而对于行向量则应该写在左边。通过这种方式将数乘法和矩阵乘法看成同一个东西。

例1：数域F上的标准线性空间 $|F^n$ ， $V:=|F^n=F\ X\ F\ X...X\ F$

加法： $[v_1\ v_2\ ......\ v_n]^T+[w_1\ w_2\ ......\ w_n]^T=[v_1+w_1\ v_2+w_2\ ......\ v_n+w_n]^T$

数乘法： $[v_1\ v_2\ ......\ v_n]^T*k=[v_1*k\ v_2*k\ ......\ v_n*k]^T$

从一个数域出发，按照如上方式，我们可以造一个标准线性空间

现在我们来证明这是个线性空间：验证上述8条运算律即可

1)加法交换律

$v+w \\=[v_1\ v_2\ ...\ v_n]^T+[w_1\ w_2\ ...\ w_n]^T \\=[v_1+w_1\ v_2+w_2\ ......\ v_n+w_n]^T \\=[w_1\ w_2\ ...\ w_n]^T+[v_1\ v_2\ ...\ v_n]^T \\=w+v$

2)加法结合律

$v+w+x \\=[v_1\ v_2\ ...\ v_n]^T+[w_1\ w_2\ ...\ w_n]^T+[x_1\ x_2\ ...\ x_n]^T \\=[v_1+w_1+x_1\ v_2+w_2+x_2\ ......\ v_n+w_n+x_n]^T \\=[x_1\ x_2\ ...\ x_n]^T+[w_1\ w_2\ ...\ w_n]^T+[v_1\ v_2\ ...\ v_n]^T \\=x+w+v$

3)有零元

设 $e=[0\ 0\ ...\ 0]^T$ ，则有

$v+e \\=[v_1\ v_2\ ...\ v_n]^T+[0\ 0\ ...\ 0]^T \\=[v_1+0\ v_2+0\ ......\ v_n+0]^T \\=[v_1\ v_2\ ...\ v_n]^T \\=v$

4)有负元

设 $w=[-v_1\ -v_2\ ...\ -v_n]^T$ ，则有

$v+w \\=[v_1\ v_2\ ......\ v_n]^T+[-v_1\ -v_2\ ...\ -v_n]^T \\=[v_1-v_1\ v_2-v_2\ ......\ v_n-v_n]^T \\=[0\ 0\ ...\ 0]^T$

5)分配率A

$(v+w)*k \\=([v_1\ v_2\ ......\ v_n]^T+[w_1\ w_2\ ......\ w_n]^T)*k \\=[v_1+w_1\ v_2+w_2\ ......\ v_n+w_n]^T*k \\=[v_1*k+w_1*k\ v_2*k+w_2*k\ ......\ v_n*k+w_n*k]^T \\=[v_1*k\ v_2*k+\ ......\ v_n*k]^T+[w_1*k\ w_2*k\ ...\ w_n*k]^T \\=[v_1\ v_2\ ......\ v_n]^T*k+[w_1\ w_2\ ......\ w_n]^T*k \\=v*k+w*k$

6)分配率B

$v*(k_1+k_2) \\=[v_1\ v_2\ ......\ v_n]^T*(k_1+k_2) \\=[v_1*(k_1+k_2) \ v_2*(k_1+k_2) \ ......\ v_n*(k_1+k_2) ]^T \\=[v_1*k_1+v_1*k_2\ v_2*k_1+v_2*k_2\ ......\ v_n*k_1+v_n*k_2]^T \\=[v_1*k_1\ v_2*k_1\ ......\ v_n*k_1]^T+[v_1*k_2\ v_2*k_2\ ......\ v_n*k_2]^T \\=v*k_1+v*k_2$

7)与数域F中元素的乘法关系

$v*(k*l) \\=[v_1\ v_2\ ......\ v_n]^T*(k*l) \\=[v_1*k*l \ v_2*k*l \ ......\ v_n*k*l ]^T \\=[v_1*k\ v_2*k\ ......\ v_n*k]^T*l \\=(v*k)*l$

8)与数域F中1的关系

$v*1\\=[v_1\ v_2\ ...\ v_n]^T*1\\=[v_1*1\ v_2*1\ ...\ v_n*1]^T\\=[v_1\ v_2\ ...\ v_n]^T\\=v$

例2：将几何空间作为线性空间(因此才会将线性空间称之为空间，将线性空间中的元素称为向量)

步骤一：定义

定义集合：V={所有有向线段的全体}

注：在有限线段的定义中，我们只考虑线段的长度和方向，不考虑起点和终点，即经过评议后可以重合的视为同一个有向线段。

定义数域：F=实数域R

定义加法：平行四边形法则

当然也可以用等价的三角形法则--

定义数乘法：使得线段同向或者反向伸缩

步骤二：验证8条运算律

1)加法交换律

2)加法结合律 (A+B)+C=A+(B+C) 利用三角形法则进行证明

3)有零元

我们知道，0向量与任意向量平行，并且长度为0，因此对于几何空间中任意一个有向线段，加上0向量后不发生任何变化。

4)有负元

取与A向量同长度却反向的有向线段为-A，则二者的和为A+(-A)，以图可以表示为如下形式：

可以看到A加上它的负元后，得到的新向量的起点和终点一致，即为0向量。

5)分配率A (A+B)*k=A*k+B*k(以k=2为例)

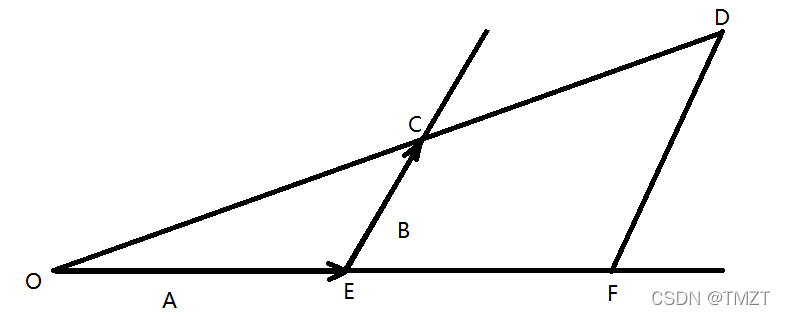
A=OE，延长OE两倍至点F，过F做FD//EC，交OC的延长线与点D，因FD//EC，因此有三角形相似：OEC～OFD。于是有OC//OD=EC//FD=OE//OF=1/2。因而有：

(A+B)*2=(OE+EC)*2=OC*2=OD

A*2+B*2=OE*2+EC*2

又因为FD//EC，且|FD|=2*|EC| (这里笔者用||表示取长度)，我们对V的定义中规定只看方向和长度，不关注起点和终点，因此有EC*2=FD，因而上式可以转化为：

A*2+B*2=OE*2+EC*2=OF+FD=OD

故可证明(A+B)*2=A*2+B*2

6)分配率B $A*(k_1+k_2)=A*k_1+A*k_2$

对于一个有向线段A来说， $A*(k_1+k_2)$ 是将A沿着原方向变为原来长度的 $(k_1+k_2)$ 倍， $A*k_1+A*k_2$ 是将在 $A*k_1$ 的基础上沿着原方向增长 $A*k_2$ ，显然二者是等价的。

7)与数域F中元素的乘法关系

对于一个有向线段A来说，A*(k*l)是将A沿着原方向变为原来长度的k*l倍，(A*k)*l是将A*k沿着原方向变为原来长度的l倍，显然二者是等价的。

8)与数域F中1的关系

很显然，对于任何一个有向线段A，A*1结果都是A本身。

例3：函数空间 $F(I,R^n)$

步骤一：定义

V： $V=F(I,R^n)$

F：是一组函数的集合，F中的每一个向量值函数可以将一个从定义域I中的数映射为一个n维向量。

例如 $F([0,1],R^2)$ ，那么属于它的一个向量值函数可以定义为如下

$f\epsilon F,F=[f_1(x)\ f_2(x)]^T=[sin(x)\ \frac{1}{2}x]^T,x\epsilon [0,1]$

注意，这一个f只是F中的一个元素而已，而F是很多个f的集合。

I：函数作用的定义区间，如I=(0,1)

R：实数域

+：加法

$f+g\\=[f_1(x)\ f_2(x)\ ...\ f_n(x)]^T+[g_1(x)\ g_2(x)\ ...\ g_n(x)]^T\\=[f_1(x)+g_1(x)\ f_2(x)+g_2(x)\ ...\ f_n(x)+g_n(x)]^T$

*：数乘

$f*k\\=[f_1(x)\ f_2(x)\ ...\ f_n(x)]^T*k\\=[f_1(x)*k\ f_2(x)*k\ ...\ f_n(x)*k]^T$

步骤二：验证8条运算律

1)加法交换律

$f+g \\=[f_1(x)\ f_2(x)\ ...\ f_n(x)]^T+[g_1(x)\ g_2(x)\ ...\ g_n(x)]^T \\=[f_1(x)+g_1(x)\ f_2(x)+g_2(x)\ ...\ f_n(x)+g_n(x)]^T \\=[g_1(x)\ g_2(x)\ ...\ g_n(x)]^T+[f_1(x)\ f_2(x)\ ...\ f_n(x)]^T \\=g+f$

2)加法结合律

$(f+g)+h \\=([f_1(x)\ f_2(x)\ ...\ f_n(x)]^T+[g_1(x)\ g_2(x)\ ...\ g_n(x)]^T)+[h_1(x)\ h_2(x)\ ...\ h_n(x)]^T \\=[f_1(x)+g_1(x)\ f_2(x)+g_2(x)\ ...\ f_n(x)+g_n(x)]^T+[h_1(x)\ h_2(x)\ ...\ h_n(x)]^T \\=[f_1(x)+g_1(x)+h_1(x)\ f_2(x)+g_2(x)+h_2(x)\ ...\ f_n(x)+g_n(x)+h_n(x)]^T \\=[f_1(x)\ f_2(x)\ ...\ f_n(x)]^T+[g_1(x)+h_1(x)\ g_2(x)+h_2(x)\ ...\ g_n(x)+h_n(x)]^T \\=[f_1(x)\ f_2(x)\ ...\ f_n(x)]^T+([g_1(x)\ g_2(x)\ ...\ g_n(x)]^T+[h_1(x)\ h_2(x)\ ...\ h_n(x)]^T) \\=f+(g+h)$

3)有零元

设 $e=[0\ 0\ ...\ 0]^T$ ，则有

$f+e \\=[f_1(x)\ f_2(x)\ ...\ f_n(x)]^T+[0\ 0\ ...\ 0]^T \\=[f_1(x)+0\ f_2(x)+0\ ...\ f_n(x)+0]^T \\=[f_1(x)\ f_2(x)\ ...\ f_n(x)]^T \\=f$

4)有负元

设 $g=[-f_1(x)\ -f_2(x)\ ...\ f_n(x)]^T$ ，则有

$f+g \\=[f_1(x)\ f_2(x)\ ...\ f_n(x)]^T+[-f_1(x)\ -f_2(x)\ ...\ -f_n(x)]^T \\=[f_1(x)-f_1(x)\ f_2(x)+-f_2(x)\ ...\ f_n(x)+-f_n(x)]^T \\=[0\ 0\ ...\ 0]^T \\=e$

5)分配率A

$(f+g)*k \\=([f_1(x)\ f_2(x)\ ...\ f_n(x)]^T+[g_1(x)\ g_2(x)\ ...\ g_n(x)]^T)*k \\=[f_1(x)+g_1(x)\ f_2(x)+g_2(x)\ ...\ f_n(x)+g_n(x)]^T*k \\=[f_1(x)*k+g_1(x)*k\ f_2(x)*k+g_2(x)*k\ ...\ f_n(x)*k+g_n(x)*k]^T \\=[f_1(x)*k\ f_2(x)*k\ ...\ f_n(x)*k]^T+[g_1(x)*k\ g_2(x)*k\ ...\ g_n(x)*k]^T \\=[f_1(x)\ f_2(x)\ ...\ f_n(x)]^T*k+[g_1(x)\ g_2(x)\ ...\ g_n(x)]^T*k \\=f*k+g*k$

6)分配率B

$f*(k_1+k_2) \\=[f_1(x)\ f_2(x)\ ...\ f_n(x)]^T*(k_1+k_2) \\=[f_1(x)*(k_1+k_2) \ f_2(x)*(k_1+k_2)\ ...\ f_n(x)*(k_1+k_2)]^T \\=[f_1(x)*k_1+f_1(x)*k\ f_2(x)*k_1+f_2(x)*k_2\ ...\ f_n(x)*k_1+f_n(x)*k_2]^T \\=[f_1(x)*k_1\ f_2(x)*k_2\ ...\ f_n(x)*k_n]^T+[f_1(x)*k_2\ f_2(x)*k_2\ ...\ f_n(x)*k_2]^T \\=[f_1(x)\ f_2(x)\ ...\ f_n(x)]^T*k_1+[f_1(x)\ f_2(x)\ ...\ f_n(x)]^T*k_2 \\=f*k_1+f*k_2$

7)与数域F中元素的乘法关系

$f*(k*l) \\=[f_1(x)\ f_2(x)\ ...\ f_n(x)]^T*(k*l) \\=[f_1(x)*(k*l) \ f_2(x)*(k*l)\ ...\ f_n(x)*(k*l)]^T \\=[f_1(x)*k*l\ f_2(x)*k*l\ ...\ f_n(x)k*l]^T \\=[f_1(x)*k\ f_2(x)*k\ ...\ f_n(x)*k]^T*l \\=([f_1(x)\ f_2(x)\ ...\ f_n(x)]^T*k)*l \\=(f*k)*l$

8)与数域F中1的关系

$f*1 \\=[f_1(x)\ f_2(x)\ ...\ f_n(x)]^T*1 \\=[f_1(x)*1 \ f_2(x)*1\ ...\ f_n(x)*1]^T \\=[f_1(x)\ f_2(x)\ ...\ f_n(x)]^T \\=f$

2.线性空间维数问题

定义：向量组及向量组拼成的抽象矩阵

设V是F上的线性空间，V中的有限序列 $v_1,v_2,...,v_n$ 称为V中的一个向量组，向量组按顺序排成的矩阵称为向量组拼成的抽象矩阵。

举个例子： $v_i=[x_i_1\ x_i_2\ ...\ x_i_n]^T$ ，可定义抽象矩阵 $A=[v_1\ v_2\ ...\ v_n]^T$ 。

2.1线性相关

线性相关性理论：我们上面的表示形式都是为了利用几何空间来研究线性空间，那么能不能类比几何空间的坐标系来得到一种东西，作为表示其他量的基础呢？

定义：向量组的线性相关性

(1)向量组 $\alpha_1,\alpha_2...,\alpha_p$ 线性相关的条件是，存在一组不全为0的数 $k_i\epsilon F,i=1,...,P$ ，使得

$\alpha_1k_1+\alpha_2k_2+...+\alpha_nk_n=0$

<=>

矩阵表述：存在 $K=[k_1\ k_2\ ...\ k_n]^T!=0$ ， $[k_1\ k_2\ ...\ k_n]^T\epsilon F^n$ ， $A=[\alpha_1\ \alpha_2\ ...\ \alpha_n]$ ，有

$AK=0$

即线性方程组有非零解

(2)向量组 $\alpha_1,\alpha_2...,\alpha_p$ 线性无关，则下式当且仅当 $k_1=k_2=...=k_n=0$ 时成立

$\alpha_1k_1+\alpha_2k_2+...+\alpha_nk_n=0$

<=>

矩阵表述：对于 $K=[k_1\ k_2\ ...\ k_n]^T!=0$ ， $[k_1\ k_2\ ...\ k_n]^T\epsilon F^n$ ， $A=[\alpha_1\ \alpha_2\ ...\ \alpha_n]$ ，当且仅当 $K=0$ 时有

$AK=0$

即线性方程组只有零解

2.2向量组之间的线性表示

A.向量的线性表示

若存在 $k_1,k_2,...,k_p\epsilon F$ ，使得

$\beta = \alpha_1k_1+\alpha_2k_2+...+\alpha_pk_p$

则称 $\beta$ 可由 $\alpha_1,\alpha_2,...,\alpha_n$ 线性表示。

矩阵形式：

$AX=[\alpha_1\ \alpha_2\ ...\ \alpha_p][x_1\ x_2\ ...\ x_p]^T=\beta$

即非齐次线性方程组存在解(是不是零解无所谓，有解就行)。

B.向量组之间的线性表示

如果每一个 $\beta_i$ 都可由 $\alpha_1,\alpha_2,...,\alpha_n$ 线性表示，则称 $\beta_1,\beta_2,...,\beta_q$ 可由 $\alpha_1,\alpha_2,...,\alpha_n$ 线性表示。

矩阵形式：

$AX\\=[\alpha_1\ \alpha_2\ ...\ \alpha_p][[x_{11}\ x_{21}\ ...\ x_{p1}]^T\ [x_{12}\ x_{22}\ ...\ x_{p2}]^T\ ...\ [x_{1q}\ x_{2q}\ ...\ x_{pq}]^T]\\=[\beta_1 \beta_2\ ...\ \beta_q]$

即上述矩阵方程有解(是不是零解无所谓，有解就行)。

**C.线性表示的传递性(设下述向量的维度均为t*1)**

$\alpha_1,\alpha_2,...,\alpha_p<=>\{\alpha_i\}$

$\beta_1,\beta_2,...,\beta_q<=>\{\beta_j\}$

$\gamma_1,\gamma_2,...,\gamma_r<=>\{\gamma_k\}$

若 $\{\beta_j\}$ 可由 $\{\alpha_i\}$ 线性表示，若 $\{\gamma_k\}$ 可由 $\{\beta_j\}$ 线性表示，则可以推出 $\{\gamma_k\}$ 可由 $\{\alpha_i\}$ 线性表示。

证明：设 $A=\{\alpha_1\ \alpha_2\ ...\ \alpha_m\},B=\{\beta_1\ \beta_2\ ...\ \beta_s\},C=\{\gamma_1\ \gamma_2\ ...\ \gamma_n\}$

若 $\{\beta_j\}$ 可由 $\{\alpha_i\}$ 线性表示，则

$A_{t*m}X_{m*s}=B_{t*s}......(1)$

上述矩阵方程有解。

同理，若 $\{\gamma_k\}$ 可由 $\{\beta_j\}$ 线性表示，则

$B_{t*s}Y_{s*n}=C_{t*n}......(2)$

上述矩阵方程有解。

现在我们要证明 $\{\gamma_k\}$ 可由 $\{\alpha_i\}$ 线性表示，即

$C_{t*n}=A_{t*m}Z_{m*n}......(3)$

有解。

将(2)带入(1)，有

$C_{t*n}=B_{t*s}Y_{s*n}=A_{t*m}X_{m*s}Y_{s*n}=A_{t*m}Z_{s*n},Z=XY$

得证。

D.向量组的极大线性无关子组(线性无关的生成子组)

子组：从母序列中挑出一个子序列(序列是要求在原来集合中可以不连续的)构成向量组，这个向量组就是原来母序列的子组。

设母组 $\{\alpha_1\ \alpha_2\ ...\ \alpha_n\}$ 子组 $\{\beta_1\ \beta_2\ ...\ \beta_s\}$

注1：对于一个向量组来说，如果交换两个向量的位置，那么交换前后就不是同一个向量组了，也就是说要考虑向量的顺序。

注2:这边只是对向量组的定义，没有其它约束，也就是说，可以两个位置的向量相同，也可以是有零向量。

极大线性无关子组：

1）是一个子组

2）满足线性无关

3）极大性：满足极大，即加一个任意向量都会变成相关

注：关于条件2）和3）可以做转化

2）+3）=2）+3‘），其中

3’）生成性：对于任意的 $\alpha_i\epsilon \{\alpha_1\ \alpha_2...\ \alpha_n\}$ ，都可由 $\{\beta_1\ \beta_2\ ...\ \beta_s\}$ 线性表示

充分性：

因为极大性，所以我们可以知 $\{\beta_1\ \beta_2\ ...\ \beta_s\ \alpha_i\}$ 线性相关，即任意 $\alpha_i$ 可由 $\{\beta_1\ \beta_2\ ...\ \beta_s\}$ 线性表示。

必要性：

因为生成性，所以任意 $\alpha_i$ 可由 $\{\beta_1\ \beta_2\ ...\ \beta_s\}$ 线性表示，也就是说加一个任意向量都会变成相关，即证明了极大性。

证毕。

笛卡尔坐标系就是空间的生成子组。

命题：母组可由其极大线性无关子组线性表示。(生成性)

E.极大线性无关组的秩

同一个母组可以有多个极大线性无关子组，但是总归要有某种不变的东西，就是子组所有的向量个数，称之为极大线性无关子组的秩。

定理：向量组的极大线性无关子组不是唯一的，但是不同的的子组拥有的向量个数是唯一的。

证明：设母组为 $\alpha_i\epsilon \{\alpha_1\ \alpha_2...\ \alpha_n\}$ (记为A)，从其中选取两个极大线性无关子组分别为 $\{\beta_1\ \beta_2\ ...\ \beta_s\}$ (记为B)，和 $\{\gamma_1\ \gamma_2\ ...\ \gamma_t\}$ (记为C)，向量均为m*1维。

反证法：不妨设s<t，那么，由于 $\{\beta_1\ \beta_2\ ...\ \beta_s\}$ 是极大无关子组，因此可以表示母组，那么可知

$BX=A$ 有解(这个由极大无关子组的性质保证)

其中X的每一列有如下对应关系

$x_{1j}\beta_1+x_{2j}\beta_2+...+x_{1s}\beta_s=\alpha_j,1<=j<=n$

同时，由于 $\{\gamma_1\ \gamma_2\ ...\ \gamma_t\}$ 是满足的子组，因此一定有

$AY=C$ 有解(这个由母组和子组的关系保证)

$y_{1j}\alpha_1+y_{2j}\alpha_2+...+y_{1n}\alpha_n=\gamma_j,1<=j<=t$

[注]：一个简单的理解方式就是我们将 $\{\gamma_1\ \gamma_2\ ...\ \gamma_t\}$ 对应到 $\alpha_i\epsilon \{\alpha_1\ \alpha_2...\ \alpha_n\}$ 中相同的向量系数设置为1，其他设置为0。也就是说，母组一定可以表示子组。

将 $BX=A$ 带入 $AY=C$ 则有

$BXY=BZ=C,Z=XY$

即

$B_{m*s}Z_{s*t}=C_{m*t}$ 有解

引理：扁的齐次线性方程组必有非零解

由条件s<t，即Z是长扁型矩阵(行数小于列数)，那么有BZ=C一定有非零解

从方程组角度看，行代表的是方程，列代表是的未知数，那么行数小于列数即等价于方程个数小于未知数个数，即为不定方程，即方程无法确定唯一的一组解，此处可以证明一下：用数学归纳法

1.当s=1，此时t>=2，即一个方程组，但有两个以上的未知数，即方程可以表示为如下形式

$ax+by+cz+...=0$

分情况讨论

A.a=0，可取x=1,y=0,z=0,...

B.a!=0，可取x=-b/a,y=1,z=0,...

2.假设s<=k成立，证s=k+1成立，此时t>=k+2

$ZW=\begin{bmatrix} z_{1,1} & z_{1,2} & ... & z_{1,t} \\ z_{2,1} & z_{2,2} & ... & z_{2,t} \\ ... & ... & ... & ...\\ z_{k+1,1} & z_{k+1,2} & ... & z_{k+1,t} \end{bmatrix}W=0$

分情况讨论

A.若 $z_{1,1}=z_{2,1}=...=z_{k+1,1}=0$ ，则根据上述，可取解

$w_1=1,w_2=w_3=...=w_t=0$

B.若 $z_{1,1},z_{2,1},...,z_{k+1,1}$ 不全为0，则至少有一个不为0，不妨设 $z_{i,1}!=0$ ，那么可利用高斯消元法使得 $z_{j,1}=0,j!=i$ ，再交换第1行和第i行，那么也就是说，从第二行到第k+1行只有 $w_2-w_t$ 的约束，那么就正好对应了s=k时的情况，根据数学归纳法的假设，我们可知一定存在一组解 $w_2,w_3,...,w_t$ 。此时回代第一个方程，即

$z_{1,1}w_1+z_{2,2}w_2+...+z_{1,t}w_t=0$ ，则可以解出 $x_1$ ，即可证是有解的。

通过上面的努力，我们已经证得ZW=0存在非零解。我们可以对BZ=C两边同乘W，则有BZW=CW。我们上面已经证明，ZW=0存在非零解，那么我们就取那个非零解，则有BZW=B(ZW)=0，更进一步，我们得到，CW=0且W是非零向量，而CW的含义就是C的各个列向量(即从母组中取出的一个极大无关子组)按照W的各个分量进行线性组合，由于这些列向量满足线性无关，因此当CW=0时应有W=0，与条件矛盾，即s<t不成立。同理也可推s>t也不成立。

[注]：高斯消元法是同解变化，即消元前后解的结果不变。

定义：向量组的秩rank就是向量组的极大线性无关组所含有向量的个数，它的大小并不依赖于无关组的挑选方式。

2.3基与坐标

现在我们可以考虑如何将代数转换到几何空间中去了。在几何空间中，我们描述位置常用的是笛卡尔坐标系，那么在代数空间中我们也需要定义这样一套标准，称之为基。

定义：有限维线性空间的基、坐标

V是数域F上的线性空间，如果有正整数n以及V中的向量组 $\alpha_1,\alpha_2,...,\alpha_n$ ，使得

1)向量组 $\alpha_1,\alpha_2,...,\alpha_n$ 线性无关

2)生成性-任意一个 $\alpha\epsilon V$ ，均可由 $\{\alpha_i\}$ 线性表示。即

$\alpha=\alpha_1k_1+\alpha_2k_2+...+\alpha_nk_n=[\alpha_1\ \alpha_2\ ...\ \alpha_n][k_1\ k_2\ ...\ k_n]^T$

则称V是n维线性空间，向量组 $\alpha_1,\alpha_2,...,\alpha_n$ 成为V的一个基(坐标系)， $[k_1\ k_2\ ...\ k_n]^T$ 称为 $\alpha\epsilon V$ 沿着基 $\alpha_1,\alpha_2,...,\alpha_n$ 的坐标向量，由基构成的矩阵 $[\alpha_1\ \alpha_2\ ...\ \alpha_n]$ 叫做基矩阵。

[抽象向量]=[基矩阵][坐标向量]

注：线性空间的维数与构成线性空间的向量的维数不是一回事，前者等价于空间的基的秩，后者则说的是空间的每一个向量有多少个分量。

命题：有限维线性空间维数的唯一性

设 $\alpha_1,\alpha_2,...,\alpha_n$ 以 $\beta_1,\beta_2\ ...\ \beta_m$ 分别是V的两个基，则有n=m。

借助同一个母组的极大线性无关子组具有相同的向量个数来证明，要证极大线性无关子组，只要证

以下证明把V看成母组，则

1)是子组：因为这两个组都是从V中挑选出来的向量构成的，因此一定是是子组

2)线性无关：由于这两个组都是基，因此本身就满足线性无关

3)极大性-不便证明也可以转换成生成性：基的定义中包含了V中所有向量都可以用基来表示

因此这两个组都是母组V的极大线性无关子组，因此自然有n=m。

定理(基或者说坐标系)实现抽象线性空间到标准线性空间之间的一一对应。

$\sigma:S_1->S_2$ ，称 $s_2$ 为 $s_1$ 的像， $s_1$ 为 $s_2$ 的原像。

1.满射-对任意的 $s_2\epsilon S_2$ ，存在 $s_1\epsilon S_1$ ，使得 $\sigma(s_1)=s_2$ ；即至少有一个 $s_1$ ，有 $s_1->s_2$

2.单射-若 $s_1\epsilon S_1,s_{1'}\epsilon S_1$ ，有 $\sigma(s_1)=s_2,\sigma(s_{1'})=s_2$ ，则必有 $s_1=s_{1'}$ ；对于一个 $s_1->s_2$ ， $s_1$

是确定的

也就是说，一一对应可以表述为如下形式：

满射：对于 $S_2$ 中的任意一个元素 $s_2$ ，在 $S_1$ 中都可以找到其原像 $s_1$ ；

单射：对于 $S_1$ 中的任何两个不同的元素，其在 $S_2$ 中的像也不可能相同。

方程解的角度：我们可以把 $\sigma(s)=t$ 看做一个方程， $t\epsilon S_2,s\epsilon S_1$ ，则对于任意一个 $t\epsilon S_2$ ，方程都有且仅有一个解。

逆映射的角度：存在一种映射 $\tau :S_2->S_1$ ，满足

A. $\tau(\sigma(s_1))=s_1$ 即是 $S_1$ 上的恒等映射

B. $\sigma(\tau(s_2))=s_2$ 即是 $S_2$ 上的恒等映射

则称 $\tau$ 是 $\sigma$ 的逆映射。

由于一一映射理论的存在，我们可以考虑把一种数据从一种形式迁移到另一种形式下，再来研究他们的关系，即用熟悉的形式研究不熟悉的数据。

证明：

V是n维线性空间， $\alpha_1,\alpha_2,...,\alpha_n$ 是V的一个基

构建一个映射 $\sigma:V->F^n$ ，用元素形式表述为 $v|->[k_1\ k_2\ ...\ k_n]^T$

这里， $k\epsilon F^n$ 是一个向量v在这组基下的坐标；即这里的映射为V中的向量映射成这个向量的坐标。

1.验证满射：对像找其原像，即任意一个 $k\epsilon F^n$ ，都至少能找到一个 $v\epsilon V$ 与之对应

不妨任取 $v\epsilon V$ ，则有

$v \\=AK \\=\alpha_1k_1+\alpha_2k_2+...+\alpha_nk_n \\=[\alpha_1\ \alpha_2\ ...\ \alpha_n][k_1\ k_2\ ...\ k_n]^T$

即任意一个n元数组都有资格成为坐标，对应的向量就是对这个基使用这个n元数组中与基向量对应的系数进行线性组合得到的向量。

2.验证单射：相同的像，他们的原像也相同

不妨设存在另一个 $v'$ ，相同的像说明 $v'$ 的坐标向量也是 $K$ ，那么现在就要证明 $v=v'$ 。

采用反证法，不妨设 $v!=v'$ ，则

$v=\alpha_1k_1+\alpha_2k_2+...+\alpha_nk_n$

$v'=\alpha_1k_1+\alpha_2k_2+...+\alpha_nk_n$

$v-v'=v=\alpha_1(k_1-k_1)+\alpha_2(k_2-k_2)+...+\alpha_n(k_1-k_1)=0$

显然假设 $v!=v'$ 是错误的。

2.3.1 $F^n$ 的标准基与一般基

标准基： $F^n$ 的标准基： $e_1=[1\ 0\ 0\ ...\ 0]^T,e_2=[0\ 1\ 0\ ...\ 0]^T,...,e_n=[0\ 0\ 0\ ...\ 1]^T$

证明：

1.无关性：若 $e_1k_1+e_2k_2+...+e_nk_n=0$ ，则

$e_1k_1+e_2k_2+...+e_nk_n=[k_1\ k_2\ ...\ k_n]^T=0$

也即

$k_1=k_2=...=k_n=0$

故这组基向量线性无关。

矩阵角度：即要证 $[e_1\ e_2\ ...\ e_n]X=0$ 只有零解

由于 $[e_1\ e_2\ ...\ e_n]=I_n$ 为单位矩阵，因此 $[e_1\ e_2\ ...\ e_n]X=I_nX=X$ ，又 $[e_1\ e_2\ ...\ e_n]X=0$ ，故

$X=0$

注：[1]标准基拼成的基矩阵是单位矩阵

[2]单位矩阵的列向量组是标注基向量组

2.可表示性：对于任意的 $v\epsilon F^n$ ， $v$ 都可以写成标准基向量的线性组合

不妨设 $v=[v_1\ v_2\ ...\ v_n]^T$ ，则显然

$v=e_1v_1+e_2v_2+...+e_nv_n$

矩阵角度：即要证 $[e_1\ e_2\ ...\ e_n]X=v$ 有解

由于 $[e_1\ e_2\ ...\ e_n]=I_n$ 为单位矩阵，因此

$I_nX=v=>X=v$

注：任意向量在标准基下的坐标就是它自己

任何一个抽象的有限维线性空间，经过建立坐标系(找一组基)，就可以同构于(一一映射)为坐标空间。

一般基： $\alpha_1,\alpha_2,...,\alpha_m\epsilon F^n$ 构成基础的充要条件是向量组的秩(极大线性无关组所含向量个数)为n<=>向量组中的向量线性无关。

$A=[\alpha_1\ \alpha_2\ ...\ \alpha_n]$

列秩=行秩=秩

行秩：行向量组的极大线性无关组所含向量个数。

列秩：列向量组的极大线性无关组所含向量个数。

证明：线性方程组Ax=b有解的充要条件是rank(系数矩阵)=rand(A)=rank(增广矩阵)=rank(A|b)

由于 $\alpha_1,\alpha_2,...,\alpha_m$ 是 $F^n$ 的一个基，因此秩应该与 $F^n$ 的标准基相同，为n，即m=n。

那么显然A是满秩方阵，(A|b)的大小为n*(n+1)，因为行秩最大为n，故rank(A|b)<=n，而rank(A|b)>=rank(A)=n，因此有rank(A|b)=n=rank(A)，因此方程组Ax=b有解。

现在我们从线性空间的角度看待方程组有解问题： $Ax=b$ 求解就是求b向量沿着A的列向量组展开的坐标向量。

2.3.2 例：无限维空间

F[x]={f| f ∈ Func(F,F) 且 f 可写成多项式}

Func(F,F)：表示函数空间，第一个F表示自变量从F中取值，第二个F表示因变量也落在F中。

Fn[x]={次数<n，以F中的数为系数的多项式}

F：数域

F[x]：数域F上的(系数全部来自于F)以x为未定元的多项式全体

Fn[x]：数域F上的(系数全部来自于F)以x为未定元的最高次数<n的多项式全体

多项式的全体构成的空间是线性空间：

A.对加法封闭

$f_=a_0x^0+a_1x^1+...+a_{n-1}x^{n-1}$

$g_=b_0x^0+b_1x^1+...+b_{m-1}x^{m-1}$

$f+g=f_=(a_0+b_0)x^0+(a_1+b_1)x^1+...+(a_m+b_m)x^{m-1}+...+a_{n-1}x^{n-1},m<n$

B.对数乘封闭

$f_=a_0x^0+a_1x^1+...+a_{n-1}x^{n-1}$

$k*f_=ka_0x^0+ka_1x^1+...+ka_{n-1}x^{n-1},k\epsilon F$

八条运算律验证：(多项式属于算式，算式一定符合这八条，笔者就不证了-。-)

1)加法交换律

2)加法结合律

3)有零元

4)有负元

5)分配率A

6)分配率B

7)与数域F中元素的乘法关系

8)与数域F中1的关系

为方便起见，我们将F取为实数域R，Rn[x]是n维的，但R[x]不是有限维的(我们称之为无限维)。

证明：Rn[x]是n维的，则可取"向量组"(也就是多项式组) $x^0,x^1,...,x^{n-1}$

注：此处选取的是多项式函数而不是单独一个数，即上面的多项式组的每一个元素对应一种映射

$\\x^0=1*x^0+0*x^1+...+0*x^{n-1}\\x^1=0*x^0+1*x^1+...+0*x^{n-1}\\...\\x^{n-1}=0*x^0+0*x^1+...+1*x^{n-1}$

$x^0,x^1,...,x^{n-1}$ 是Rn[x]的一个基

1.无关性

即证如果 $a_0x^0+a_1x^1+...+a_{n-1}x^{n-1}=0$ ，则

$a_i=0,i=0,1...,n-1$

注： $a_0x^0+a_1x^1+...+a_{n-1}x^{n-1}=0$ 表示的是左端部分等于右端的0函数，即x代入任意的值，左边式子得到的结果都是0。

由定义，可以任意地代入n个值(此处给x代入的是值而不是函数)， $x=1,2,...,n$ ，有

$\begin{bmatrix} 1^0 & 1^1 & ... & 1^{n-1}\\ 2^0 & 2^1 & ... & 2^{n-1}\\ ... & ... & ... & ...\\ n^0 & n^1 & ... & n^{n-1} \end{bmatrix}[a_0\ a_1\ ...\ a_{n-1}]^T=Xa=[0\ 0\ ...\ 0]^T$

根据范德蒙行列式的性质，有

$det|X|!=0$

因此X可逆，即 $a=X^-1[0\ 0\ ...\ 0]^T=0$ ，即 $a_i=0,i=0,1...,n-1$

2.可表示性

对于任意f∈Rn[x]，根据多项式的定义，有

$f=a_0x^0+a_1x^1+...+a_{n-1}x^{n-1}=[a_0\ a_1\ ...\ a_{n-1}][x^0\ x^1\ ...\ x^{n-1}]^T$

证明R[x]不是有限维的，首先回忆如何证明Rn[x]是有限维的，实际上就是找到一组基。那么我们可以这样证明R[x]不是有限维的，对于R[x]中的任意一个向量组，都不是基，即要么不满足无关性要么无法表示任意的向量。

取一组"向量组" $f_1,f_2,...,f_N$ ，记 $d_i=d(f_i),i=1,2,...,N$ 为函数 $f_i$ 中的最高次，再取 $d=max\{d_1,d_2,...,d_N\}$ ，可证明 $x^{d+1}\epsilon IF[x]$ 不能由这组向量线性表示，否则若

$x^{d+1}=a_1f_1(x)+a_2f_2(x)+...+a_Nf_N(x)$

按照x的次数整理右端可得

$x^{d+1}=b_0x^0+b_1x^1+...+b_dx^d$

于是可得

$b_0x^0+b_1x^1+...+b_dx^d-1x^{d+1}=0$

此处的0是常值0函数。

类似上面的推理，可以任取d+1个值带入给x，可证得所有的系数都为0，这显然与最后一个为-1的系数矛盾，因而不具有可表示性。

因而证明全体多项式构成的空间不是有限维空间。

注：向量是欧几里得空间对元素的叫法，但由于多项式空间是线性空间，因此我们也可以将它的元素叫做向量。

课外内容：如何从映射的角度理解加法

加法是一个映射，也就是一个二元函数，从集合中有顺序的取两个元素，也可以理解为从VxV的笛卡尔积集合中取一个元素，利用加法就可以算出另一个属于V中的元素，即定义如下：

$\sigma:V\ X\ V->V$

例如：定义二元函数

$z=f(x,y)=xy+\frac{1}{2}x^2$

这可以被视为一种映射

$(x,y)|->z,R^2->R$

因此加法就是一个二元映射。

同理，数乘法也可以理解为是 $V\ X\ F->V$ ，F是数域。

WALL-SQ

关注

7
点赞
踩
21

收藏

觉得还不错? 一键收藏
1
评论
矩阵论-线性空间与线性映射

0.导言矩阵论真难啊QaQ，做个笔记，以哈工大严质彬老师的讲解为例，很推荐，讲的非常不错~传送门：矩阵论_哔哩哔哩_bilibili1.线性空间与线性映射给定非空集合V和域F，若存在映射：则称为V上的加法；若存在映射：则称为V上的数乘。1)注1：域：是一个系统，其中定义了两种运算-加法和乘法，若这两个运算在这个系统上满足一些比较好的性质，是的+的逆运算-可以在该系统上能进行，*的逆运算/也可以在该系统上进行，则称该运算系统为域。换句话说，域是一个满足+、-、*、/
复制链接

扫一扫