贪心算法的应用

贪心算法：

贪心算法主要有贪心选择性质和最优子结构性质

贪心选择性质：

所求问题的整体最优解可以通过一系列局部最优的选择，在贪心算法中，仅在当前状态下做好最好选择，即局部最优选择。动态规划算法通常以自底向上的方式解各子问题,而贪心算法则通常以自顶向下的方式进行,以迭代的方式做出相继的贪心选择,每做出一次贪心选择就将所求问题简化为规模更小的子问题。

最优子结构性质：

当一个问题的最优解包含其子问题的最优解时,称此问题具有最优子结构性质。在活动安排问题中,其最优子结构性质表现为:若A是关于E的活动安排问题的包含活动1的一个最优解,则相容活动集合A'=A-{1}是关于E'={i∈E:si≥f}的活动安排问题的一个最优解。各个子问题的最优解之和构成了原问题的最优解。

活动安排问题

活动安排问题是可以用贪心算法有效求解的很好的例子。该问题要求高效地安排一系列争用某一公共资源的活动。贪心算法提供了一个简单、有效的方法,使得尽可能多的活动能兼容地使用公共资源。
设有n个活动的集合E一{1,2，…,n},其中,每个活动都要求使用同―资源,如演讲会场等,而在同一时间内只有一个活动能使用这一资源。

算法思想：

        用集合A存储所选择的活动。活动 i 在集合A中,当且仅当A[i]的值为true。变量 j 用以记录最近一次加入A的活动。由于输入的活动按其结束时间的非减序排列,Fj总是当前集合A中所有活动的最大结束时间
        贪心算法,开始选择活动1,并将 j 初始化为1。然后依次检查活动 i 是否与当前已选择的所有活动相容。若相容则将活动 i 加入已选择活动的集合A 中;否则，不选择活动 i ,而继续检查下一活动与集合A中活动的相容性。由于Fj总是当前集合A中所有活动的最大结束时间,故活动i与当前集合A中所有活动相容的充分且必要的条件是其开始时间Si，不早于最近加入集合A 的活动 j 的结束时间Fi ,即Sj≥Fi;。若活动i与之相容,则 i 成为最近加入集合A中的活动,并取代活动j的位置。

该算法的贪心选择的意义是使剩余的可安排时间段极大化,以便安排尽可能多的相容活动。

根本问题是在所给的活动集合中选出最大的相容活动子集合

public static int intgreedySelector(int []s,int []f,boolean []a){
        int n=s.length-1;
        a[1]=true;
        int j=1;
        int count=1;
        for (int i=2;i<=n;i++){
            if (s[i] > f[j]){
                a[i]=true;
                j=i;
                count++;
            }else {
                a[i]=false;
            }
        }
        return count;
    }

例如,设待安排的11个活动的开始时间和结束时间按结束时间的非减序排列如下:

选择了活动1后,原问题简化为对E中所有与活动1相容的活动进行活动安排的子问题。也就是说,若A是原问题的最优解,则A' = A - {1}是活动安排问题E'={i∈E:Si,≥Fi}的最优解。

背包问题

0-1背包问题（动态规划问题）与背包问题（贪心算法问题）的区别

给定n种物品和一个背包。物品i的重量是Wi,其价值为Vi,背包的容量为C。应如何选择装入背包的物品,使得装入背包中物品的总价值最大?
0-1背包问题：在选择装人背包的物品时,对每种物品i只有两种选择,即装入背包或不装入背包。不能将物品i装入背包多次﹐也不能只装入部分的物品i。

对于0-1背包问题,设A是能够装入容量为C的背包的具有最大价值的物品集合,则Aj=A - {j}是

n - 1个物品1,2，…,j - 1,j + 1,…,n可装入容量为C - Wj的背包的具有最大价值的物品集合。

---

背包问题：与0-1背包问题类似,所不同的是在选择物品i装入背包时,可以选择物品i的一部分,而不一定要全部装入背包,1 ≤ i ≤ n。
对于背包问题,若它的一个最优解包含物品 j ,则从该最优解中拿出所含的物品j的那部分重量w ,剩余的将是n - 1个原重物品1,2，…,j - 1,j+1,…,n以及重为Wj - w的物品 j 中可装入容量为C - w的背包且具有最大价值的物品。

算法步骤：

首先计算每种物品单位重量的价值Vi / Wi，然后依贪心选择策略,将尽可能多的单位重量价值最大的物品装入背包。若将这种物品全部装入背包后,背包内的物品总重量未超过C,则选择单位重量价值次高的物品并尽可能多地装入背包。若装入某一物品时背包的容量不够，则需要对最后装入的物品进行部分装入。依此策略一直地做下去,直到背包装满为止。

public static class Element{
        float w;
        float v;
        int i;

        public Element(float ww,float vv,int ii){
            w=ww;
            v=vv;
            i=ii;
        }

    }

    //x[]表示物品的放入状态
    public static float knaspack(float c,float []w,float []v,float []x){
        int n=v.length;
        Element []d = new Element[n];
        for (int i=0;i<n;i++){
            d[i] =new Element(w[i],v[i],i);
        }
        MergeSort.mergeSort(d);//对物品结构体根据v[i]/w[i]从大到小排序
        float opt=0;
        int i;
        for (i=0;i<n;i++) x[i]=0;//状态初始化
        for (i=0;i<n;i++){
            if (d[i].w>c) break;  //该放入的物品重量超过剩余容量，只能放入一部分，解决措施见下
            x[d[i].i] = 1;//该放入的物品能全部放入
            opt+=d[i].v;
            c-=d[i].w;
        }
        //此时i为无法整体放入的物品编号
        if (i<n){//该放入的物品重量超过剩余容量，只能放入一部分，解决措施见下
            x[d[i].i]=c/d[i].w;//放入部分的占比
            opt+=x[d[i].i]*d[i].v;
        }
        
        return opt;
    }

单源最短路径问题

给定带权有向图G=(V,E),其中每条边的权是非负实数。另外,还给定V中的一个顶点,称为源。现在要计算从源到所有其他各顶点的最短路长度。这里路的长度是指路上各边权之和。这个问题通常称为单源最短路径问题

Dijkstra算法是解单源最短路径问题的贪心算法。其基本思想是,设置顶点集合S并不断地做贪心选择来扩充这个集合。一个顶点属于集合S当且仅当从源到该顶点的最短路径长度已知。初始时,S中仅含有源。设u是G的某一个顶点,把从源到u且中间只经过S中顶点的路称为从源到u的特殊路径,并用数组dist记录当前每个顶点所对应的最短特殊路径长度。Dijkstra算法每次从V - S中取出具有最短特殊路长度的顶点u ,将u添加到s 中,同时对数组dist进行必要的修改。一旦S包含了所有V中顶点,dist就记录了从源到所有其他顶点之间的最短路径长度。

上述Dijkstra算法只计算出从源顶点到其他顶点间的最短路径长度。如果还要求相应的最短路径,可以用算法中数组 prev记录的信息找出相应的最短路径。算法中数组 prev[i] 记录的是从源到顶点的最短路径上i的前一个顶点。初始时,对所有i≠1,置prev[i]=v。在 Dijkstra算法中更新最短路径长度时,只要dist[u]+c[u][i]<dist[i]时，就置prev[i]=u。当Dijkstra算法终止时,就可以根据数组 prev找到从源到﹔的最短路径上每个顶点的前一个顶点,从而找到从源到i的最短路径。

//以下数组均从下表为1开始
    /*
    v 源点
    a[][]各边的之间的权值，若无连线则为9999；
    dist[i]表示i到v的最短路径长度
    prev[i]表示最短路径是点i的前一个顶点
     */
    public static void Dijkstra(int v,float [][]a,float[] dist,int []prev){
        int n=dist.length-1;
        if(v < 1||v > n) return;//原点从点集中选择
        boolean []s = new boolean[n+1];//s[i]表示顶点i是否进入S集合
        //初始化
        for (int i=1;i<=n;i++){
            dist[i]=a[v][i];
            s[i]=false;
            if (dist[i]==9999) prev[i]=0;//与源点没有连线，距离为∞
            else prev[i]=v;
        }
        dist[v]=0;s[v]=true;//初始将源点放入集合s
        for (int i=1;i<n;i++){

            //找出每一轮dist最小的，放入集合s
            float temp = 9999;
            int u=v;
            for (int j=1;j<=n;j++) {
                if (!s[j] && (dist[j] < temp)) {//找最小的并且没有在集合s中的
                    u = j;
                    temp = dist[j];
                }
                s[u] = true;//将最小的放入集合s
            }
                //让新进入集合s的点，作为源点进行对dist、prev的更新
                for (int j=1;j<=n;j++){
                    if ((!s[j])&&(a[u][j]<9999)){//点j不在集合s中并且与此时的源点之间有连线
                        float newdist=dist[u]+a[u][j];
                        if (newdist<dist[j]){//更新
                            dist[j]=newdist;
                            prev[j]=u;
                        }
                    }
                }

        }
    }

最小生成树

设G=(V,E)是无向连通带权图,即一个网络。E中每条边(v,w)的权为c[v][w]。如果G的子图G'是一棵包含G的所有顶点的树,则称G'为G的生成树。生成树上各边权的总和称为该生成树的耗费。在G的所有生成树中,耗费最小的生成树称为G的最小生成树。

Prim算法

设G=(V,E)是连通带权图,V={1,2,…,n)。

构造G的最小生成树的Prim 算法的基本思想是:首先置S={1},然后，只要S是V的真子集,就进行如下的贪心选择:选取满足条件i∈S,j∈V-S,且 c[i][j]最小的边,将顶点 j 添加到 S 中。这个过程一直进行到S=V时为止。在这个过程中选取到的所有边恰好构成G的一棵最小生成树。
 

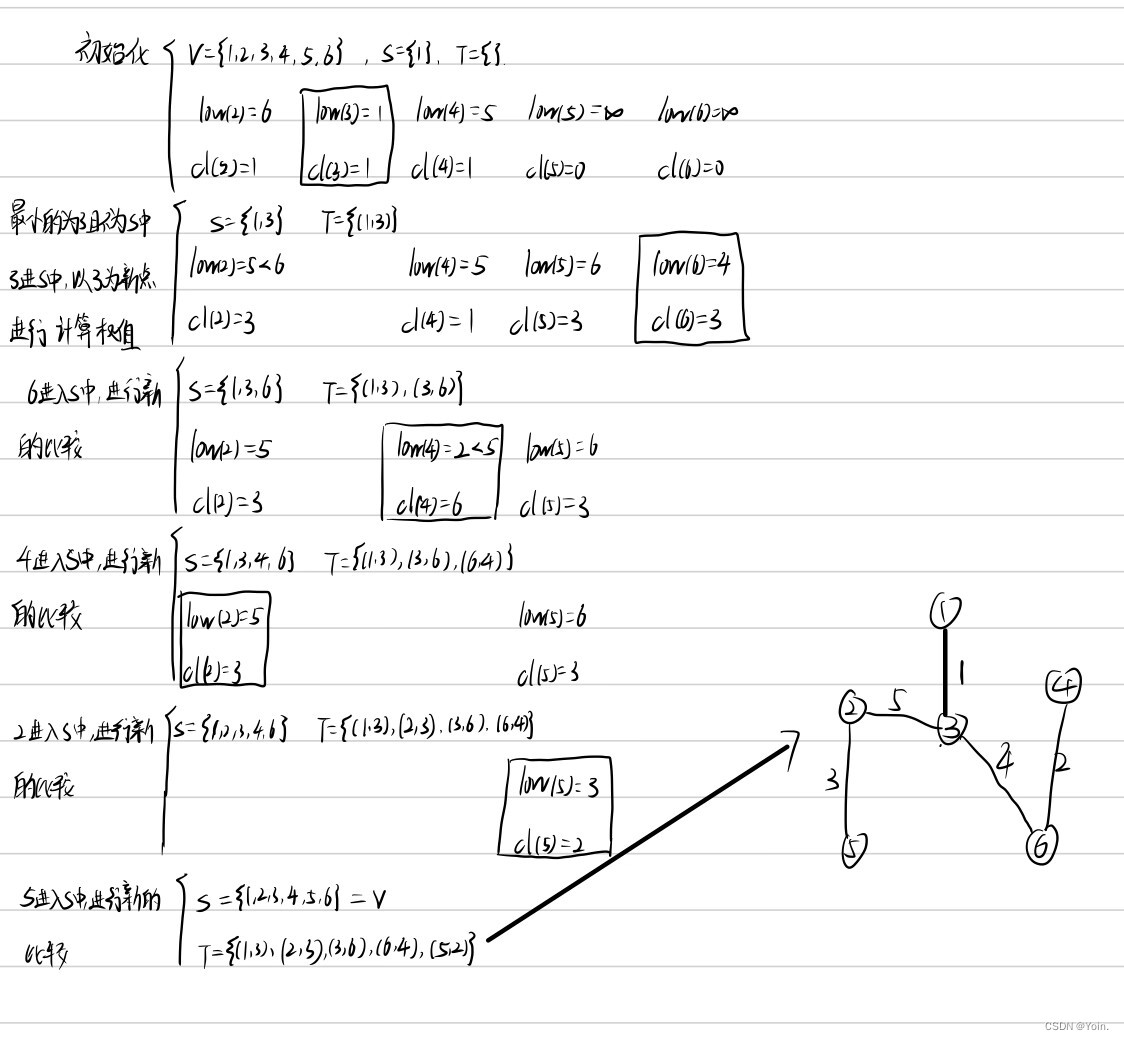
    public static void prim(int n,float[][]c){
        float [] lowest = new float[n+1];
        int [] closest = new int[n+1];
        boolean []s = new boolean[n+1];
        
        //初始化
        s[1]=true;//集合s初始只有1
        for (int i=2;i<=n;i++){
            lowest[i]=c[1][i];//所有v-s中的点的lowest均为与点1的权值
            closest[i]=1;//所有v-s中的点与s中的邻接点均为1
            s[i]=false;//v-s中的点均不在s中
        }
        //将v-s中的点放入s
        for (int i=1;i<n;i++){//直至s=v，即将v-s中n-1个点放入s中
            float min = Float.MAX_VALUE;
            int j=1;//指向s中的点
            for (int k=2;k<=n;k++){//找到所有v-s中与1放入最小权值的点k，将k放入s中
                if ((lowest[k]<min)&&(!s[k])){
                    min=lowest[k];
                    j=k;//指向s中新入的点
                }
            }
            s[j]=true;//点j放入s中

            //更新lowest、closest
            for (int k=2;k<=n;k++){
                if ((c[j][k]<lowest[k])&&(!s[k])){//c[j][k]表示新加入s的点与v-s中各点的权值与s中旧点进行对比
                    lowest[k]=c[j][k];
                    closest[k]=j;
                }
            }
        }
    }

Kruskal算法

给定无向连通带权图G=(V,E),V={1,2,…,n}。Kruskal算法构造G的最小生成树的基本思想是：

首先将G的n个顶点看成n个孤立的连通分支。将所有的边按权从小到大排序。然后从第一条边开始,依边权递增的顺序查看每一条边,并按下述方法连接两个不同的连通分支:当查看到第k条边(v,w)时,如果端点v和 w分别是当前网个不回的连通分支T1和T2中的顶点时,就用边(v,w)将T1和T2连接成一个连通分支,然后继续查看第k＋1条边;如果端点v和w在当前的同一个连通分支中,就直接再查看第k＋1条边。这个过程一直进行到只剩下一个连通分支时为止。此时,这个连通分支就是G的一棵最小生成树。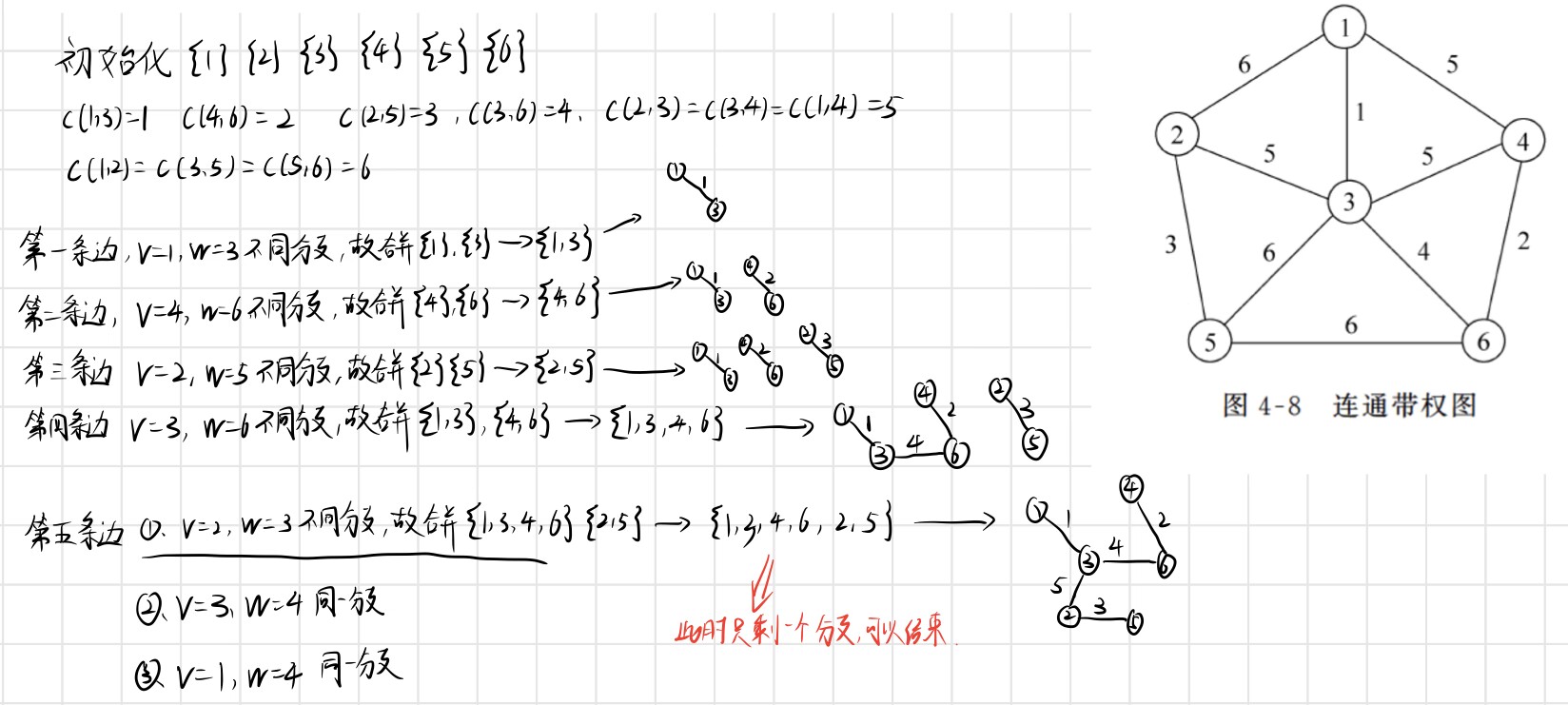 

 流水调度问题

        n个作业{1,2,…,n}要在由两台机器M1和M2组成的流水线上完成加工。每个作业加工的顺序都是先在M1上加工,然后在M2上加工。M1和M2加工作业 i 所需的时间分别为ai和 bi (1≤i≤n)。流水作业调度问题要求确定这n个作业的最优加工顺序,使得从第一个作业在机器M1上开始加工,到最后一个作业在机器M2上加工完成所需的时间最少。
        直观上，一个最优调度应使机器M1,没有空闲时间,且机器M2的空闲时间最少。在一般情况下,机器M2上会有机器空闲和作业积压两种情况。
        设全部作业的集合为N={1,2,…,n}。S是N的作业子集。在一般情况下,机器M1,开始加工.S中作业时,机器M2还在加工其他作业,要等时间 t 后才可利用。将这种情况下完成S中作业所需的最短时间记为T(S,t)。流水作业调度问题的最优值为T(N,0)

public static class Element implements Comparable{
        int key;
        int index;
        boolean job;
        
        public Element(int kk,int ii,boolean jj){
            key = kk;
            index = ii;
            job = jj;
        }
        @Override
        public int compareTo(Object x) {
            int xkey =((Element)x).key;
            if (key<xkey) return -1;
            if (key==xkey) return 0;
            return 1;
        }
    }
    //求最优调度时间、
    /*
    a 表示M1上个作业的运行时间
    b 表示M2上各作业的运行时间
    c 表示最有调度顺序
     */
    public static int flowshop(int []a,int []b,int []c){
        int n = a.length;
        Element []d = new Element[n];
        for (int i=0;i<n;i++){
            
            int key;
            if (a[i]>b[i]) key = b[i];
            else  key = a[i];
            boolean job=false;
            if (a[i]<=b[i]) job = true;
            d[i]=new Element(key,i,job);
        }
        MergeSort.mergetSort(d);
        int j = 0;
        int k = n-1;
        
        for (int i=0;i<n;i++){
            if (d[i].job) c[j++] = d[i].index;
            else c[k--] = d[i].index;
        }
        j=a[c[0]];
        k=j+b[c[0]];
        for (int i=0;i<n;i++){
            j+=a[c[i]];//在M1上的总作业时间
            if (j<k) k=k+b[c[i]];
            else k=j+b[c[i]];
        }
        return k;
    }