12.讲排序（下）：如何用快排思想在O(n)内查找第K大元素

归并排序和快速排序都用到了分治思想。问题：如何在O(n)的时间复杂度内查找一个无序数组中的第K大元素？

1. 归并排序的原理 Merge sort

如图所示：

分治算法一般都是用递归来实现的。分治是一种解决问题的处理思想，递归是一种编程技巧，这两者并不冲突。

归并排序的性能分析

• 归并排序是稳定算法
• 归并排序的时间复杂度,O(nlogn)。（master公式分析）
• 归并排序的空间复杂度，O(n)。

2.快速排序的原理

快排的思想是这样的：如果要排序数组中下标从p到r之间的一组数据，我们选择p到r之间的任意一个数据作为pivot（分区点）。

我们遍历p到r之间的数据，将小于pivot的放到左边，将大于pivot的放到右边，将pivot放到中间。经过这一步骤之后，数组p到r之间的数据就被分成了三个部分，前面p到q-1之间都是小于pivot的，中间是pivot，后面的q+1到r之间是大于pivot的。

递推公式：
quick_sort(p…r) = quick_sort(p…q-1) + quick_sort(q+1, r)

终止条件：
p >= r

// 快速排序，A是数组，n表示数组的大小
quick_sort(A, n) {
  quick_sort_c(A, 0, n-1)
}
// 快速排序递归函数，p,r为下标
quick_sort_c(A, p, r) {
  if p >= r then return
  
  q = partition(A, p, r) // 获取分区点
  quick_sort_c(A, p, q-1)
  quick_sort_c(A, q+1, r)
}

分区函数：

partition(A, p, r) {
  pivot := A[r]
  i := p
  for j := p to r-1 do {
    if A[j] < pivot {
      swap A[i] with A[j]
      i := i+1
    }
  }
  swap A[i] with A[r]
  return i

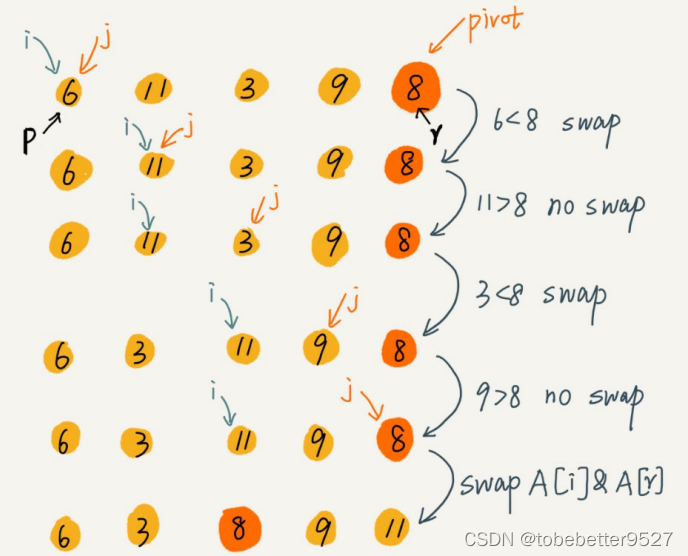
快速排序的性能分析

• 快速排序是不稳定的
• 快速排序的时间复杂度,O(nlogn)，最差O(n^2). 为避免出现最差情况，有一些手段合理选择pivot。
• 快速排序的空间复杂度，O(1)，原地排序。

3.解答开篇

解答开篇的问题：O(n)时间复杂度内求无序数组中的第K大元素。比如，4， 2， 5， 12， 3这样一组数据，第3大元素就是4。

我们选择数组区间A[0…n-1]的最后一个元素A[n-1]作为pivot，对数组A[0…n-1]原地分区，这样数组就分成了三部分，A[0…p-1]、A[p]、A[p+1…n-1]。

如果p+1=K，那A[p]就是要求解的元素；如果K>p+1, 说明第K大元素出现在A[p+1…n-1]区间，我们再按照上面的思路递归地在A[p+1…n-1]这个区间内查找。同理，如果K<p+1，那我们就在A[0…p-1]区间查找。

第一次分区查找，我们需要对大小为n的数组执行分区操作，需要遍历n个元素。第二次分区查找，我们只需要对大小为n/2的数组执行分区操作，需要遍历n/2个元素。依次类推，分区遍历元素的个数分别为、n/2、n/4、n/8、n/16.……直到区间缩小为1。

如果我们把每次分区遍历的元素个数加起来，就是：n+n/2+n/4+n/8+…+1。这是一个等比数列求和，最后的和等于2n-1。所以，上述解决思路的时间复杂度就为O(n)。

你可能会说，我有个很笨的办法，每次取数组中的最小值，将其移动到数组的最前面，然后在剩下的数组中继续找最小值，以此类推，执行K次，找到的数据不就是第K大元素了吗？

不过，时间复杂度就并不是O(n)了，而是O(K * n)。你可能会说，时间复杂度前面的系数不是可以忽略吗？O(K * n)不就等于O(n)吗？

这个可不能这么简单地划等号。当K是比较小的常量时，比如1、2，那最好时间复杂度确实是O(n)；但当K等于n/2或者n时，这种最坏情况下的时间复杂度就是O(n2)了。