游戏厅

游戏厅

问题描述

虚拟现实游戏的火爆导致在魔法学院附近出现了许多的游戏厅。虽然如此，但由于学院的学员众多（<= 3000），所以抢到游戏机玩的难度非常之大。学院到游戏厅的路是错综复杂的，以至于到一个自己想去的游戏厅都有非常多的线路可以选择，而路线的长度又不相同，这样就决定了要花费的时间，因此想要尽快到达，选择一条最佳的线路是很有必要的。

为了简化问题，我们把学院与周边的游戏厅看做图中的顶点，学校与游戏厅，游戏厅与游戏厅之间的线路看作边，每个边都有一个权，表示我们走完这条路的时间，由于放学人流量大，如果反向走会比较危险，因此这是一个有向图。设学院在S点，想要去的游戏厅在T点。你的任务就是选择一条最佳路线，是的从学校到目的地游戏厅的时间最短，你只需输出最短到达时间即可。

输入文件

输入文件共有M+2行数据，第一行两个整数N、M，表示点数和边数。

然后M行每行3个正整数（u，v，t），表示有一条可由u到v耗时为t的边。最后一行两个正整数S，T。

输出文件

输出文件只要一行，一个整数表示最短时间。如果S，T之间不存在通路，则输出“No Solution！”（双引号不输出，“！”为西文标点）

输入样例

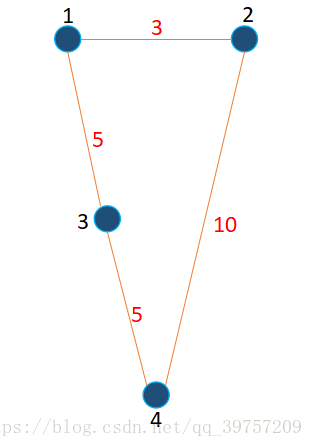
4 4

1 2 3

2 4 10

1 3 5

3 4 5

1 4

输出样例

10

数据规模

对于30%的数据保证有1<N<=1000,1<=M<=1000;

对于全部的数据保证有1<N<=10000,1<=M<=100000。

算法分析

采用前向星+Bellman-ford即可

前向星表示法是把所有的边集中在一起形成一个边列表，比如说表示第i条边（u，v）=w就应当分别把起点、终点、权值存在三个数组中但下标相同。星形表示法分为前向心和后向星。前向星按照起始点从小到大排序，前向星的好处是比链表节省时间和空间，只要不增加或者删除边，就能很快找到从一个点出发的所有边。除了不能直接用起点终点定位以外，前向星几乎是完美的。

例如有一个图结点有100000个，普通的矩阵存图存的即使100000×100000。而前向星是保存边，一共定义三个数组a[i]、b[i]和e[i]，它们分别表示第i条边的起点编号、第i条边的终点编号、第i条边的权值。

于是我们可以就可以这样读数据：

cin >> n >> m;
for(int i = 1; i <= m; i++)
cin >> a[i] >> b[i] >> e[i];

然后对数组a进行排序，即sort（a+1，a+m+1），为的是让这些起始编号有序（让终止编号有序也可以，不过一般都是排起始编号）。

这就是前向星了，结构非常简单，空间复杂度视边的个数（也就是m）而定。

采用前向星表示法，设三个数组x，y，e，分别保存每条边的起点编号、终点编号和所需的时间（权值），再设一个数组d保存到该点的最短时间，输入要查询线路s，t，首先令要查询那条边的起点的时间为0，即d[s] = 0，令其他点的时间为最大值，通过循环判断，替换每个点的最短时间，最后判断要查询该线路的终点标号最短路时间是否为最大值，如果为最大值，则不存在通路，否则就输出最短路径。

#include <iostream>
#include <string.h>
#include <string>
#include <set>
#include <stack>
#include <algorithm>
using namespace std;

int x[10000+1], y[10000+1], e[10000+1];//分别保存每条边的起点，终点以及相应的时间
int d[10000+1];//保存每个点的最短时间
int n, m, s, t;//点的个数，边的条数，查询边的起点编号和终点编号

void init(){
	cin >> n >> m;
	int i;
	for(i = 1; i <= m; i++){
		cin >> x[i] >> y[i] >> e[i];
	}
	sort(x+1, x+m+1);//对数组x排序，使得起始编号有序
	cin >> s >> t;
}

void bellman_ford(int s){
	int i, j;
	for(i = 1; i <= n; i++){
		d[i] = INT_MAX;
	}
	d[s] = 0;
	for(i = 1; i <= n; i++){
		for(j = 1; j <= m; j++){
			if(d[x[j]] != INT_MAX && d[y[j]] > d [x[j]] + e[j])//判断终点的时间是否大于起点时间加上该边的时间，如果是就替换（替换最短到达时间）
				d[y[j]] = d[x[j]] + e[j];
		}
	}
	if(d[t] != INT_MAX)
		cout << d[t] << endl;
	else//如果查询边的终点最短时间为最大值则不存在通路
		cout << "No Solution!" << endl;
}

int main(){
	init();
	bellman_ford(s);
	system("pause");
	return 0;
}