C/C++ 二叉树及其三种遍历（递归+非递归）+层次

实例代码参考学长https://blog.csdn.net/plm199513100

#include<iostream>
using namespace std;
#include<stdio.h>
#include<stack>
#include<queue>
//二叉树的存储结构
typedef struct BiTNode
{
    int data;       //数据域
    struct BiTNode *lchild,*rchild;     //指针域

}BiTNode,*BiTree;

//初始化,树的一个结点
void InitTree(BiTree &T,int x)
{
    T->data = x;
    T->lchild = NULL;
    T->rchild = NULL;
}

//递归创建一棵二叉树
void CreateTree(BiTree &T)
{
    int val = 0;
    cin>>val;
    if(val == -1)   //如果是-1代表此分支终止
        T = NULL;
    else
    {
        T = new BiTNode;
        InitTree(T,val);
        CreateTree(T->lchild);
        CreateTree(T->rchild);
    }
}
//先序遍历二叉树(递归)
void PreOrder(BiTree T)
{
    if(T != NULL)
    {
        cout<<T->data<<" ";
         PreOrder(T->lchild);
         PreOrder(T->rchild);
    }
}


//中序遍历二叉树(递归)
void InOrder(BiTree T)
{
    if(T != NULL)
    {
        InOrder(T->lchild);
        cout<<T->data<<" ";
        InOrder(T->rchild);
    }
}
//后序遍历二叉树(递归)
void PostOrder(BiTree T)
{
    if(T!=NULL)
    {
        PostOrder(T->lchild);
        PostOrder(T->rchild);
        cout<<T->data<<" ";
    }
}
//先序遍历二叉树（非递归）根左右
void PreOrder2(BiTree T)
{
    stack<BiTNode*> _sta;
    BiTNode * p = T;
    while( !_sta.empty() || p != NULL )
    {
        if(p != NULL)
        {
            _sta.push(p);     //根元素入栈
            cout<<p->data<<" ";   /**元素入栈的次序是一样的，不同的只是输出元素的语句所在位置不一样而已*/
            p = p->lchild;      //指向左子树
        }
        else
        {
            p = _sta.top();
            _sta.pop();          //子树的左子树为空，弹出此时该子树的根结点
            p = p->rchild;      //指向右子树
        }
    }
}

//中序遍历二叉树（非递归）
void InOrder2(BiTree T)
{

    stack<BiTNode *> _sta;
    BiTNode * p = T;

    while(!_sta.empty() || p!=NULL)
    {
        if(p != NULL)
        {
            _sta.push(p);   //根元素入栈
            p = p->lchild;      //转向其左子树
        }
        else
        {
            p = _sta.top();
            cout<<p->data<<" ";
            _sta.pop();         //子树的左子树为空，弹出此时该子树的结节点
            p = p->rchild;
        }
    }
}
/**
后序跟前两个不同，它必须判断是否是从左子树还是右子树返回，如果是左子树的
返回，则需要继续遍历其右子树。如果是右子树返回那么可以push出对应元素。
所以要多了一些操作加一区分是左子树还是右子树的返回
这里用的是从反面考虑，我们先是按（根右左的遍历）相当于将左右子树对换位置，将结果存在另一个栈中，
再依次出栈就得到了后序遍历了，当然还有其他方法，比如添加标志位确定是从左子树还是右子树返回来的
*/
//后序遍历的非递归算法，借助两个栈（根右左）遍历存到栈中再依次出栈
void PostOrder2(BiTree T)
{
    int val;
    stack<BiTNode *> _sta;
    stack<int> sta_val;
    BiTNode * p = T;
    while( !_sta.empty() || p != NULL )
    {
        if(p != NULL)
        {
            _sta.push(p); //根元素入栈
            sta_val.push(p->data);  //根值入栈
            p = p->rchild;          //转入右子树
        }
        else  //右子树为空，转到左子树
        {
            p = _sta.top();     //返回根结点
            _sta.pop();        //子树的右子树为空，弹出此时该子树的根节点
            p = p->lchild;
        }
    }
    while(!sta_val.empty())
    {
         cout<<sta_val.top()<<" ";
         sta_val.pop();
    }
}
//层次遍历算法，借助队列实现
void LevelOrder(BiTree T)
{
    queue<BiTNode*> _qlist;
    BiTree p = T;
    _qlist.push(p);       //根结点入队
    while(!_qlist.empty())
    {
        cout<<_qlist.front()->data<<" ";
        if(_qlist.front()->lchild!=NULL)
            _qlist.push(_qlist.front()->lchild);   //左子树不空左子树入队

        if(_qlist.front()->rchild!=NULL)
            _qlist.push(_qlist.front()->rchild);  //右子树不空，右子树入队

         _qlist.pop();   //队头元素出队
    }
}
int main()
{
    BiTree T;
    CreateTree(T);
    PreOrder2(T);
    cout<<endl;
    PostOrder2(T);
    cout<<endl;
    LevelOrder(T);
}

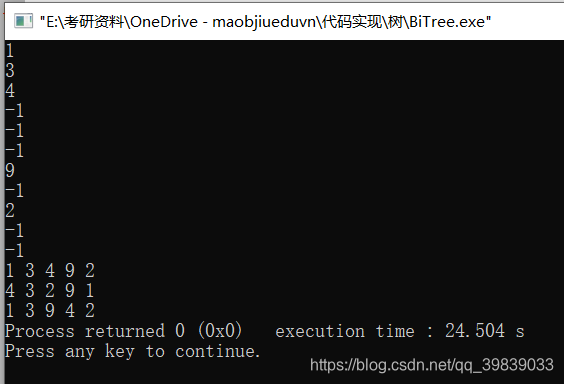
运行实例：