[matlab]DDA原理画直线、圆弧测试

zackkkkkkkk

已于 2023-05-06 18:19:19 修改

阅读量3.1k

点赞数 25

文章标签： matlab 算法

于 2023-02-13 01:46:30 首次发布

本文链接：https://blog.csdn.net/qq_39892910/article/details/128978782

版权

本文探讨了使用STM32微控制器进行直线和圆弧插补的方法，包括DDA算法的实现，分析了独立和关联轴运动两种模式下的差异，以及速度和精度的影响。通过MATLAB模拟展示了不同速度和精度设置下的路径效果，讨论了如何优化算法以提高路径精度。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

打算用stm32做主控DIY台xy雕刻机，所以看了一点DDA直线插补和圆弧插补的东西，一些细节不是很懂，所以用matlab画了直线和圆弧的几种情况。代码在最后，这里的代码和数控技术的算法不一样。

DDA直线：

X,Y轴运动独立:

根据进给速度和直线信息，得从出X轴速度 $V_x=\frac{x_e}{L}V$ 和Y轴速度 $V_y=\frac{x_y}{L}V$ ，周期为常数 $\Delta t$ ，每周期X累加器增加 $\Delta x=V_x*\Delta t$ ，当累加器溢出时,向相应电机发送脉冲，Y轴也一样。

根据这个写了一个画直线的函数：

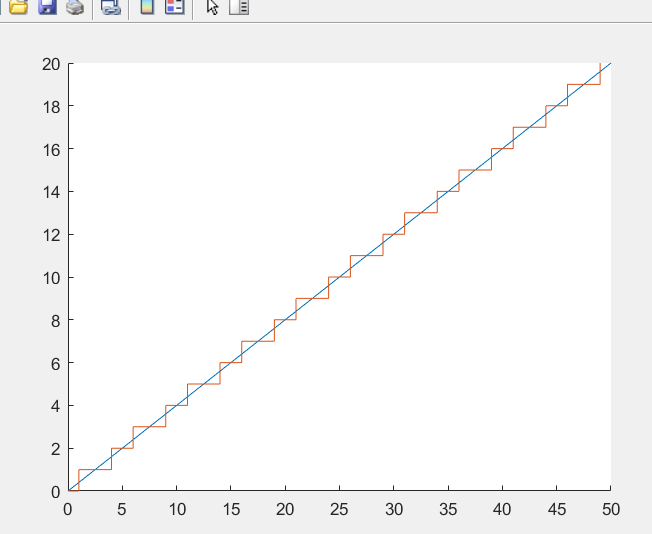
( 原点到(50,20),进给速度=0.1)

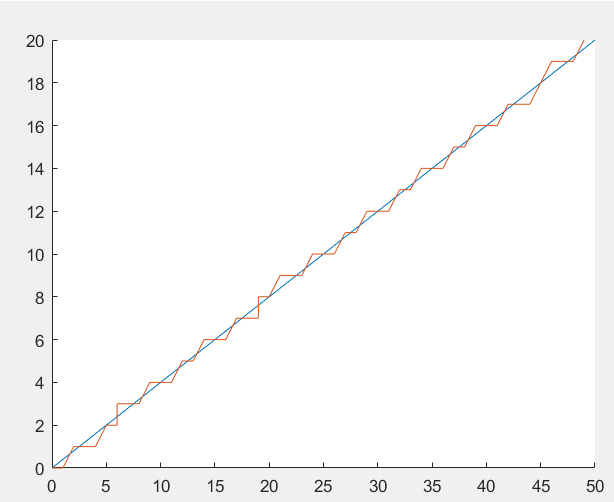
( 速度=1) (速度=2)

累加器做了半加载处理，半加载的对精度的改善相当于四舍五入，就像C语言中正浮点数四舍五入：int(5.5+0.5)。

如果进给速度太大，一个周期就会溢出太多导致画出来的直线失真严重，这跟数控技术中的不一样，数控技术的算法中 $\Delta x,\Delta y$ 满足 $\Delta x<1 , \Delta y<1$ ，这样画不会偏离太多。

X,Y轴运动关联：

上面，两轴运动独立，这里将两个轴的运动关联，这样画出来的路径就与速度无关，选一个方向，比如X轴，计算出X轴进给速度 $V_x=\frac{x_e}{L}V$ ，X累加器每个周期累加Vx，当X轴累加器溢出时，向X电机发送1个脉冲并且Y轴累加器累加 $\frac{dx}{dy}*\Delta x=\frac{\Delta y}{\Delta x}*1$ ，Y轴累加器溢出时向Y电机发送脉冲。

选位移较大的方向作为步进的方向，这样另一个轴累加值小于1。

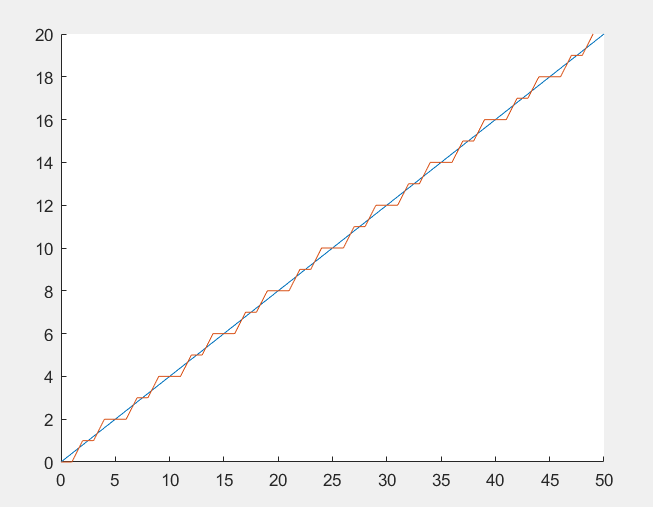
（原点到(50,20),速度=1) (速度=2）

这样画出来的路径不受程序的速度参数影响，路径与下面代码画出来的相同

 X=0:50;Y=0.4*X;plot(X,int32(Y));

如果没有半加载，那就是

X=0:50;Y=0.4*X;plot(X,floor(Y));

DDA圆弧：

X,Y轴运动独立：

推导1：

逆时针圆的参数方程：

$x=R*cos(a)$

$y=R*sin(a)$

对时间t求导：

$\frac{dx}{dt}=R*\frac{da}{dt}*-sin(a)=-\frac{V}{R}y$

$\frac{dy}{dt}=R*\frac{da}{dt}*cos(a)=\frac{V}{R}x$

(V是线速度)

有了初始坐标就能用上面的方程进行迭代(欧拉法)：

$x_{i+1}=x_i-\Delta t\frac{V}{R}y_i$

$y_{i+1}=y_i+\Delta t\frac{V}{R}x_i$

$\Delta t\frac{V}{R}$ 是常数，所以也可以写成：

$x_{i+1}=x_i-ky_i$

$y_{i+1}=y_i+kx_i$

推导2：

$|V_x|=V*sin(\alpha )=V*\frac{y}{R}=\frac{V}{R}y$

$|V_y|=V*cos(\alpha )=V*\frac{x}{R}=\frac{V}{R}x$

接下来和推导1一样，注意下符号就行。

推导3：

首先速度向量与半径垂直，那么只要将位置坐标的XY互换一下再添个符号就行

，也就是向量(X,Y)的垂直向量是(-Y,X)或(Y,-X)。

推导1和推导2推得啥?画蛇添足吗？

做了这个操作后再除以模R乘以速度V。

$|V_x|=V*\frac{y}{R}=\frac{V}{R}y$

$|V_y|=V*\frac{x}{R}=\frac{V}{R}x$

接下来和推导1一样，注意下符号就行。

与上面一样，X,Y累加器每个周期累加 $\Delta x=-ky,\Delta y=kx$ ，当累加器溢出时，向相应电机发出脉冲。

根据这个写了一个画圆的函数：

(起始于[50,0]，速度=0.5，迭代次数=400)

一次性最好只画一个象限的圆弧，再根据圆的对称性画其他象限的圆弧，这样比较容易编程，效率也高。如果一次性画整圆，那必须得处理符号问题，这使得编程更复杂，同时也拖了效率。

但为了方便观察，这里的函数能一次性画出整个圆，改变迭代次数可以改变圆弧的长度。

这里，累加器不做半加载处理，因为累加值有符号，而正浮点四舍五入与负浮点四舍五入是不同的，int(5.5+0.5)、int(-5.5-0.5)，半加载改成对累加器四舍五入后再判断溢出。

(迭代次数=8000)

迭代方程是一Z阶近似，这相当于沿着切线走，路肯定越走越宽，可以用二阶近似来提高精度。

二阶近似推导1：

$\frac{d^2x}{dt^2}=-\frac{V}{R}\frac{dy}{dt}=-\frac{V^2}{R^2}x$

$\frac{d^2y}{dt^2}=\frac{V}{R}\frac{dx}{dt}=-\frac{V^2}{R^2}y$

$x_{i+1}=x_i-\frac{\Delta t^2\frac{V^2}{R^2}}{2}x_i-\Delta t\frac{V}{R}y_i=x_i-\frac{k^2}{2}x_i-ky_i=(1-\frac{k^2}{2})x_i-ky_i$

$y_{i+1}=y_i-\frac{\Delta t^2\frac{V^2}{R^2}}{2}y_i+\Delta t\frac{V}{R}x_i=y_i-\frac{k^2}{2}y_i+kx_i=(1-\frac{k^2}{2})y_i+kx_i$

二阶近似推导2：

设 $x_i=R*cos(a)$

$x_{i+1}-x_i=R*cos(a+\Delta a) -R*cos(a)$

$=R*(cos(a)*cos(\Delta a)-sin(a)*sin(\Delta a)) -R*cos(a)$

$=x_i*cos(\Delta a)-y_i*sin(\Delta a)-x_i$

所以：

$x_{i+1}=cos(\Delta a)*x_i-sin(\Delta a)*y_i$

将cos与sin用泰勒一阶多项式替换得到之前方程：

$x_{i+1}=x_i-\Delta a*y_i$

$\Delta a=\Delta t\frac{V}{R}=k$

将cos与sin用泰勒二阶多项式替换：

$x_{i+1}=(1-\frac{\Delta a^2}{2})x_i-\Delta a*y_i$

$x_{i+1}=(1-\frac{k^2}{2})x_i-ky_i$

Y轴也一样，所以有：

$x_{i+1}=(1-\frac{k^2}{2})x_i-ky_i$

$y_{i+1}=(1-\frac{k^2}{2})y_i+kx_i$

一阶与二阶对比(紫线为二阶)：

(迭代次数=8000) ， (速度=1，迭代次数=8000)

某种隐式求解法:

将一阶方程 $x_{i+1}=x_i-ky_i$ ， $y_{i+1}=y_i+kx_i$ 改成：

$x_{i+1}=x_i-ky_i$

$y_{i+1}=y_i+kx_{i+1}$

在代码中只需要改变累加那一行的位置就可以实现。

三者对比(黑线为隐方法)：

（速度=1，迭代次数=400）(速度=1，迭代次数=8000)

隐方法看起来还可以，提高速度看看(x,y是实数)：

（速度=12.5，迭代次数=40） (迭代次数=800)

迭代次数为40时，紫线和圆严丝合缝，黑线形状变椭，迭代次数为800时，紫线已经往外走了，但黑线还在自己的轨道。

在运算量上，二阶的运算量比一阶的更多些，隐方法的与一阶的一样。

X,Y轴运动关联：

圆的标准方程：

$x^2+y^2=R^2$

对其求关于x的一、二阶导数得：

$2x+2y\frac{dy}{dx}=0$

$2+2(\frac{dy}{dx})^2+2y\frac{d^2y}{dx^2}=0$

$\frac{dy}{dx}=-\frac{x}{y}$

$\frac{d^2y}{dx^2}=-\frac{y^2+x^2}{y^3}$

x与y对称的，所以：

$\frac{dx}{dy}=-\frac{y}{x}$

$\frac{d^2x}{dy^2}=-\frac{y^2+x^2}{x^3}$

从方程上来看，x=0或y=0时会出现斜率无穷大的情况，如果在画圆弧时始终选择一个轴作为主要方向，那就会出现斜率无穷大的情况。有一个解决方法：当X坐标绝对值与Y坐标绝对值相同时交换方向，既保证了从动方向的累加量小于等1又能保证不出现斜率无穷大的情况。

根据初始坐标选择方向，根据 $\frac{dx}{dt}=-ky$ ， $\frac{dy}{dt}=kx$ 来计算XY轴速度的绝对值，选绝对值大的那个的对应轴作为主要方向，如果两绝对值相等，那就根据关于t的二阶导来判断。

比如对于初始坐标(0,50)有： $|\frac{dy}{dt}|>|\frac{dx}{dt}|$ ，所以选Y轴作为主要方向开始迭代直到 $|\frac{dy}{dt}|=|\frac{dx}{dt}|$ 或者说 $|x|=|y|$ 时，交换方向。

根据以上写了个画圆的函数：

红线为一阶，黑线为二阶，

（速度=1，迭代次数=400） (速度=12)

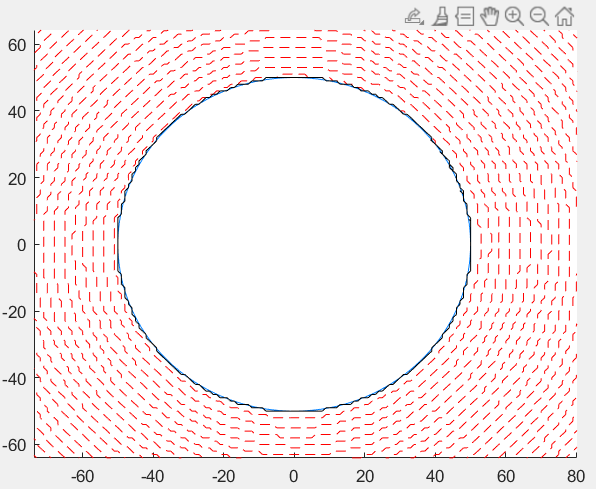
（速度=1，迭代次数=8000） (速度=12)

还是一样，画出来的路径不受程序的速度参数影响。

一阶情况下，两种圆弧积分的精确度控制：

画直线的话，其关于X或Y二阶导数恒为0，初始位置已知的情况下，X或Y一阶导数的积分与原路径是一样的。

圆方程关于X或Y二阶导不恒为0，所以用一阶导数来积分有误差，而 $\Delta x$ 和 $\Delta y$ 的取值范围是{-1,1}，这种情况下，可以调节精度但有点麻烦。

而运动独立的方法中， $\Delta y=\Delta t\frac{dy}{dt}$ ， $\Delta x=\Delta t\frac{dy}{dt}$ ，可以通过调节△t来减小误差。

当圆弧的半径较小时，运动联合方法绘制的路径将会偏离较多且无法调节精度。（这里的代码没法调节联合方法的精确度）

在独立的方法中，将速度设置得尽可能地小，来提高精度。

（虚线为联合方法，实线为独立方法）

（起始[5,0]，速度=0.005，迭代次数=40）

代码段：

function DqCir(R,pre,q)
% 此处显示有关此函数的摘要
% DCir:画象限圆
% q:象限
% R:半径
% pr:精度
% DqCir(50,0.01,1)
%   此处显示详细说明
A=pi/2*(q-1):pre:pi/2*q;
X=R*cos(A);
Y=R*sin(A);
plot(X,Y,'-','color',[0,0.5,1]);
end

DDA画直线(XY独立)

function Line_dda_1(sta,ed,v)
% 此处显示有关此函数的摘要
% Line_dda_1:DDA画直线(XY轴运动独立)
% 此处显示详细说明
% sta:起点
% ed:终点
% v:进给速度(精度)
% x,y电机一个脉冲移动1
    Del=[ed(1)-sta(1),ed(2)-sta(2)];%[△x,△y]
    if abs(Del(1))<1e-7 && abs(Del(2))<1e-7
        warning('没有输入');
        return;
    end
    vx=abs(v*Del(1)/norm(Del));%计算vx(dx)
    vy=abs(v*Del(2)/norm(Del));
    count=1;
    Inx=0.5;%累加器半装载(四舍五入)
    Iny=0.5;
    pos=sta;
    x=sta(1);
    y=sta(2);
    while 1
        Inx=Inx+vx;
        Iny=Iny+vy;
        count=count+(Inx>=1|Iny>=1);
        if Inx>=1 
            Inx=Inx-1; 
            x=x+sign(Del(1));
        end
        if Iny>=1           
            Iny=Iny-1;
            y=y+sign(Del(2));
        end
        pos(count,:)=[x,y];%记录点
        if abs(x-ed(1))<=0.5||abs(y-ed(2))<=0.5
            break;
        end
    end
    hold on
    plot([sta(1),ed(1)],[sta(2),ed(2)]);
    plot(pos(:,1),pos(:,2));
end

DDA画直线(XY关联)

function Line_dda_2(sta,ed,v)
% 此处显示有关此函数的摘要
% Line_dda_2:DDA画直线(XY轴运动关联)
% 此处显示详细说明
% sta:起点
% ed:终点
% v:进给速度
% x,y电机一个脉冲移动1
    Del=[ed(1)-sta(1),ed(2)-sta(2)];%[△x,△y]
    if abs(Del(1))<1e-7 && abs(Del(2))<1e-7
        warning('没有输入');
        return;
    end
    if abs(abs(Del(1))-abs(Del(2)))<1e-7 %abs(△x)=abs(△y)相等
        v=abs(v*Del(1)/norm(Del));%计算vm
        Flag=0;%同时移动
    elseif abs(Del(1))>abs(Del(2)) %abs(△x)>abs(△y)
        v=abs(v*Del(1)/norm(Del));
        vl=abs(Del(2)/Del(1));
        Flag=1;%主要方向为X方向
    else
        v=abs(v*Del(2)/norm(Del));
        vl=abs(Del(1)/Del(2));
        Flag=2;%主要方向为Y方向
    end
    count=1;
    Inm=0.5;%累加器半装载(四舍五入)
    Inl=0.5;
    pos=sta;
    x=sta(1);
    y=sta(2);
    while Flag~=3
        Inm=Inm+v;
        while Inm>=1
           Inm=Inm-1; 
           if Flag~=0
               x=x+sign(Del(1))*(Flag==1);
               y=y+sign(Del(2))*(Flag==2);
               Inl=Inl+vl;
               if Inl>=1
                Inl=Inl-1;
                x=x+sign(Del(1))*(Flag==2);
                y=y+sign(Del(2))*(Flag==1);
               end
           else
               x=x+sign(Del(1));%同时移动
               y=y+sign(Del(2));
           end
            count=count+1;
            pos(count,:)=[x,y];%记录点
            if count>=int32(max(abs(Del(2)),abs(Del(1))))%int32带有四舍五入
                Flag=3;%停止
                break;
            end
        end
    end
    hold on
    plot([sta(1),ed(1)],[sta(2),ed(2)]);
    plot(pos(:,1),pos(:,2));
end

(因符号的问题，画圆程序变得复杂)DDA画整圆(XY独立)

function Cirle_dda_1(R,sta,ed,v)
% Cirle_dda_1:DDA画圆弧(XY轴运动独立)
% sta:起点
% ed:迭代次数
% v:速度(精度)
% x,y电机一个脉冲移动1
% Cirle_dda_1(50,[50,0],8000,0.1);
% Cirle_dda_1(50,[0,50],8000,0.1);
% Cirle_dda_1(50,[-50,0],8000,0.1);
% Cirle_dda_1(50,[0,-50],8000,0.1);
    if abs(sta(1))<1e-7 && abs(sta(2))<1e-7
        warning('没有输入');
        return;
    end
%-----------------------一阶
    pos=[sta];
    count=1;
    x=sta(1);%X坐标
    y=sta(2);
    vx=-y/R*v;%vx(dx)
    vy=x/R*v;
    Inx=0;%符号问题，使用半加载会让程序更复杂，改成累加器四舍五入后再判断溢出
    Iny=0;  
    while 1
        Inx=Inx+vx;%累加△x
        Iny=Iny+vy;  
        count=count+(abs(Inx)+0.5>=1||abs(Iny)+0.5>=1); 
        if abs(Inx)+0.5>=1&&sign(Inx)==sign(vx)%溢出判断(四舍五入)
           x=x+sign(Inx);
           vy=vy+sign(Inx)*v/R;
           Inx=Inx-sign(Inx);
        end
        if abs(Iny)+0.5>=1&&sign(Iny)==sign(vy)
            y=y+sign(Iny); 
            vx=vx-sign(Iny)*v/R;
            Iny=Iny-sign(Iny);
        end
        pos(count,:)=[x,y];
        if count>ed
            break;
        end
    end
    hold on
    plot(pos(:,1),pos(:,2),'color',[1,0,0]);
    DqCir(R,0.01,1);
    DqCir(R,0.01,2);
    DqCir(R,0.01,3);
    DqCir(R,0.01,4);
%----------------------隐方法 
    pos=[sta];
    count=1;
    x=sta(1);%X坐标
    y=sta(2);
    vx=-y/R*v;%vx(dx)
    vy=x/R*v;
    Inx=0;%符号问题，使用半加载会让程序更复杂，改成累加器四舍五入后再判断溢出
    Iny=0;  
    while 1
        Flag=0;%溢出标志位
        Inx=Inx+vx;
        if abs(Inx)+0.5>=1&&sign(Inx)==sign(vx)%溢出判断(四舍五入)
           x=x+sign(Inx);
           vy=vy+sign(Inx)*v/R;
           Inx=Inx-sign(Inx);
           Flag=1;
        end
        Iny=Iny+vy;     
        if abs(Iny)+0.5>=1&&sign(Iny)==sign(vy)
            y=y+sign(Iny); 
            vx=vx-sign(Iny)*v/R;
            Iny=Iny-sign(Iny);
            Flag=1;
        end
        count=count+Flag;   
        pos(count,:)=[x,y];
        if count>ed
            break;
        end
    end
    plot(sta(1),sta(2),'*');
    plot(pos(:,1),pos(:,2),'color',[0,0,0]);
%----------------------二阶
    pos=[sta];
    count=1;
    x=sta(1);%X坐标
    y=sta(2);
    vx=-y/R*v;%vx(dx)
    vy=x/R*v;
    Inx=0;%符号问题，使用半加载会让程序更复杂，改成累加器四舍五入后再判断溢出
    Iny=0;  
    while 1
        Inx=Inx+vx-x*0.5*(v/R)^2;%累加
        Iny=Iny+vy-y*0.5*(v/R)^2;  
        count=count+(abs(Inx)+0.5>=1||abs(Iny)+0.5>=1); 
        if abs(Inx)+0.5>=1&&sign(Inx)==sign(vx)%溢出判断(四舍五入)
           x=x+sign(Inx);
           vy=vy+sign(Inx)*v/R;
           Inx=Inx-sign(Inx);
        end 
        if abs(Iny)+0.5>=1&&sign(Iny)==sign(vy)
            y=y+sign(Iny); 
            vx=vx-sign(Iny)*v/R;
            Iny=Iny-sign(Iny);
        end   
        pos(count,:)=[x,y];
        if count>ed
            break;
        end
    end
   plot(sta(1),sta(2),'*');
   plot(pos(:,1),pos(:,2),'color',[1,0,1]);
end

DDA画圆弧(XY关联)

function Cirle_dda_2(R,sta,ed,v)
% Cirle_dda_2:DDA画圆弧
% sta:起点
% ed:迭代次数
% v:速度
% x,y电机一个脉冲移动1
% Cirle_dda_2(50,[50,0],8000,0.1);
% Cirle_dda_2(50,[0,50],8000,0.1);
% Cirle_dda_2(50,[-50,0],8000,0.1);
% Cirle_dda_2(50,[0,-50],8000,0.1);
%-------------------一阶
    if abs(sta(1))<1e-7 && abs(sta(2))<1e-7
        warning('没有输入');
        return;
    end
    pos=[sta];
    count=1;
    x=sta(1);%X坐标
    y=sta(2);
    vx=-y/R*v;%vx(dx)
    vy=x/R*v;   
    s=sign([vx,vy]);%符号
    if  abs(abs(vx)-abs(vy))<1e-7
        Flag=(-x+vx>-y+vy)*1+(-x+vx<=-y+vy)*2;%根据二阶导判断主要方向
    elseif abs(vx)>abs(vy)
        Flag=1;%主要方向X方向
    else 
        Flag=2;%主要方向Y方向
    end
    Inl=0;%符号问题，使用半加载会让程序更复杂，改成累加器四舍五入后再判断溢出
    Inm=0;
    while Flag~=3
        Inm=Inm+vx*(Flag==1)+vy*(Flag==2); %累加
        while(abs(Inm)+0.5>=1&&sign(Inm)==sign(s(Flag)))%溢出判断(四舍五入)
           if Flag==1
               Inl=Inl-x/y*sign(Inm);
           else
               Inl=Inl-y/x*sign(Inm);
           end              
           x=x+sign(Inm)*(Flag==1);
           y=y+sign(Inm)*(Flag==2);
           vy=vy+sign(Inm)*v/R*(Flag==1);
           vx=vx-sign(Inm)*v/R*(Flag==2);
           Inm=Inm-sign(Inm);
           while(abs(Inl)+0.5>=1&&sign(Inl)==sign(s(3-Flag)))%溢出判断(四舍五入)
               x=x+sign(Inl)*(Flag==2);
               y=y+sign(Inl)*(Flag==1);
               vy=vy+sign(Inl)*v/R*(Flag==2);
               vx=vx-sign(Inl)*v/R*(Flag==1); 
               Inl=Inl-sign(Inl);
           end 
           s=sign([vx,vy]);
           if (abs(vy)>abs(vx)&&Flag==1) || (abs(vy)<abs(vx)&&Flag==2)%判断是否需要交换方向
               Inm=0;
               Inl=0;
               Flag=3-Flag;
           end
           count=count+1;   
           pos(count,:)=[x,y];
           if count>ed
                Flag=3;
                break;
           end
        end
    end
    hold on
    plot(sta(1),sta(2),'*');
    plot(pos(:,1),pos(:,2),'--','color',[1,0,0]);
    DqCir(R,0.01,1);
    DqCir(R,0.01,2);
    DqCir(R,0.01,3);
    DqCir(R,0.01,4);
%-------------------二阶
    pos=[sta];
    count=1;
    x=sta(1);%X坐标
    y=sta(2);
    vx=-y/R*v;%vx(dx)
    vy=x/R*v;   
    s=sign([vx,vy]);%符号
    if  abs(abs(vx)-abs(vy))<1e-7
        Flag=(-x+vx>-y+vy)*1+(-x+vx<=-y+vy)*2;%根据二阶导判断主要方向
    elseif abs(vx)>abs(vy)
        Flag=1;%主要方向X方向
    else 
        Flag=2;%主要方向Y方向
    end
    Inl=0;%符号问题，使用半加载会让程序更复杂，改成累加器四舍五入后再判断溢出
    Inm=0;
    while Flag~=3
        Inm=Inm+vx*(Flag==1)+vy*(Flag==2); %累加
        while(abs(Inm)+0.5>=1&&sign(Inm)==sign(s(Flag)))%溢出判断(四舍五入)
           if Flag==1
               Inl=Inl-x/y*sign(Inm)-0.5*(y^2+x^2)/y^3;
           else
               Inl=Inl-y/x*sign(Inm)-0.5*(y^2+x^2)/x^3;
           end              
           x=x+sign(Inm)*(Flag==1);
           y=y+sign(Inm)*(Flag==2);
           vy=vy+sign(Inm)*v/R*(Flag==1);
           vx=vx-sign(Inm)*v/R*(Flag==2);
           Inm=Inm-sign(Inm);
           while(abs(Inl)+0.5>=1&&sign(Inl)==sign(s(3-Flag)))%溢出判断(四舍五入)
               x=x+sign(Inl)*(Flag==2);
               y=y+sign(Inl)*(Flag==1);
               vy=vy+sign(Inl)*v/R*(Flag==2);
               vx=vx-sign(Inl)*v/R*(Flag==1); 
               Inl=Inl-sign(Inl);
           end
           s=sign([vx,vy]);
           if (abs(vy)>abs(vx)&&Flag==1) || (abs(vy)<abs(vx)&&Flag==2)%判断是否需要交换方向
               Inm=0;
               Inl=0;
               Flag=3-Flag;
           end
           count=count+1;   
           pos(count,:)=[x,y];
           if count>ed
                Flag=3;
                break;
           end
        end
    end
    plot(pos(:,1),pos(:,2),'--','color',[0,0,0]);
end