最优化建模、算法与理论（一）—— 基础知识

奶盖加芝士

已于 2022-08-05 17:32:38 修改

阅读量1.4k

点赞数 2

分类专栏：最优化建模、算法与理论文章标签：算法

于 2022-06-25 15:50:59 首次发布

本文链接：https://blog.csdn.net/qq_39916709/article/details/125378029

版权

最优化建模、算法与理论专栏收录该内容

4 篇文章 14 订阅

订阅专栏

参考书籍《最优化：建模、算法与理论》

文章目录

1 最优化

问题一般形式

min f(x)
s.t. x ∈ X 
其中 x = (x1, x2,··· , xn)T ∈ Rn 是决策变量
f : Rn → R 是目标函数
X ⊆ Rn 是约束集合或可行域，可行域包含的点称为可行解或可行点
记号 s.t. 是 “subject to”的缩写，专指约束条件

最优化算法研究基本步骤：构造最优化模型、确定最优化问题的类型和设计算法、实现算法或调用优化算法软件包进行求解

2 最优化问题的分类

按目标函数和约束函数的形式划分

线性规划：目标函数与约束函数均为线性函数
非线性规划：目标函数和约束函数中至少有一个为非线性函数
二次规划：目标函数是二次函数而约束函数是线性函数
非光滑优化：包含非光滑函数无导数优化：不能直接求导数的问题
整数规划：变量只能取整数的问题
半定规划：在线性约束下极小化关于半正定矩阵的线性函数的问题
锥规划：半定规划的广义形式

按最优解的性值划分

稀疏优化：最优解只有少量非零元素
低秩矩阵优化：最优解是低秩矩阵

连续和离散优化

连续优化问题：决策变量所在的可行集合是连续的，比如平面、区间等
离散优化问题：指决策变量能在离散集合上取值，比如离散点集、整数集等

无约束和约束优化

无约束优化：决策变量没有约束条件限制，即可行集合 X = Rn
约束优化：指带有约束条件的问题

随机和确定性

随机优化：目标或者约束函数中涉及随机变量而带有不确定性的问题
不像确定性优化：中目标和约束函数都是确定的

凸和非凸优化

凸优化：目标函数和可行域分别是凸函数和凸集
非凸优化：目标函数和可行域至少有一个不为凸
注：因为凸优化问题的任何局部最优解都是全局最优解，其相应的算法设计以及理论分析相对非凸优化问题简单很多

此外还有几何优化、二次锥规划、张量优化、鲁棒优化、全局优化、组合优化、网络规划、随机优化、动态规划、带微分
方程约束优化、微分流形约束优化、分布式优化等。

3 数学基础

这里罗列最优化常用数学概念，一些更基础的内容或者细节会注明知识点，如线性代数、数值代数、概率论等。

3.1 范数

定义 2.1 (范数) 称一个从向量空间 Rn 到实数域 R 的非负函数 || · || 为
范数，如果它满足：
(1) 正定性：对于所有的 v ∈ Rn，有 || v || ⩾ 0，且 || v || = 0 当且仅当 v = 0；
(2) 齐次性：对于所有的 v ∈ Rn 和 α ∈ R，有 || αv || = |α| || v || ；
(3) 三角不等式：对于所有的 v，w ∈ Rn，有 || v + w || ⩽ || v || + || w ||
最常用的向量范数为 ℓp 范数 (p ⩾ 1)：
$_p = (|v_1|^p + |v_2|^p + ··· + |v_n|^p) ^{\frac{1}{F}}$
当 p = ∞ 时，ℓ∞ 范数定义为： || v || ∞ = max(i) |vi|

p = 1, 2, ∞ 的情形最重要,分别记为 || · || 1 , || · || 2 和 || · || ∞

矩阵A的 l0 范数为所有元素中非零元素得个数
矩阵A的 l1 范数为所有元素的绝对值之和： $A || _1 = ∑{_{i=1}^m} ∑{_{j=1}^n} | a _{ij} |$
矩阵A的 l2 范数（又称F范数）为所有元素的平方和开根号: $_F = \sqrt{\sum{a{_{ij}^2}}}$
F范数具有正交不变性，即 $对于任意的正交矩阵U\in\mathbb{R}^{m\times{m}}，V\in\mathbb{R}^{n\times{n}}，有||UAV||{_{f}^{2}} = ||A||{_{f_’}^{2}}$

3.2 凸函数

基本定义

$f(\theta x + (1 - \theta)y) \leq \theta f(x) + (1 - \theta)f(y)，对所有x,y\in dom, 0 \leq \theta \leq 1都成立$
注：这与同济版高等数学中凸函数的定义是反的

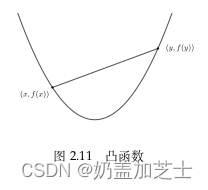
在这里插入图片描述

强凸函数

$\frac{m}{2}||x||^2，为凸函数，则称f(x)为强凸函数，其中m为强凸参数$

意义：f为强凸函数且存在最小值，则f的最小值点唯一。即f为凸函数才有可能求取全局最优解。
常见凸（凹）函数

1.仿射函数： $a^Tx +b$
2.指数函数
3.幂函数
4.负熵： $x l n x （ x > 0 ）$
5.所有范数
6.二阶导数 >0 的函数

保凸运算

$1.若f是凸函数，则\alpha f是凸函数，其中\alpha \geq{0}$
$2.若 f_1，f_2 是凸函数,则 f_1 + f_2 是凸函数$ $3. 若 f 是凸函数, 则 f (A x + b) 是凸函数$
$4.若 f_1 , f_2 , · · · , f_m 是凸函数,则 f ( x ) = max { f_1 ( x ), f_2 ( x ) , · · · , f_m ( x )}是凸函数$
$5.若对每个 y ∈ A , f ( x, y ) 关于 x 是凸函数,则g ( x ) = \sup_{y ∈A}f (x, y )是凸函数$
$6.给定函数 g : R^n → R 和 h : R → R,令 f ( x ) =h ( g ( x )) ，若g 是凸函数,h 是凸函数且单调不减,那么 f 是凸函数；若 g是凹函数，h 是凸函数且单调不增，那么 f 是凸函数$
$7.给定函数 g: R^n → R^k ,h : R^k → R, f ( x ) = h ( g ( x )) = h ( g_1 ( x ) , g_2( x ) , · · · , g_k ( x )) . 若 g_i 是凸函数，h 是凸函数且关于每个分量单调不减，那么 f 是凸函数；若g_i 是凹函数，h 是凸函数且关于每个分量单调不增，那么 f 是凸函数$
$8.若 f ( x, y ) 关于 ( x, y )整体是凸函数,C 是凸集,则g ( x ) = \inf_{y ∈ C} f ( x, y )是凸函数$
$R^n × R → R，g(x，t) = tf ( {\frac{x}{t}} )，dom g= \{(x，t)|\frac{x}{t}\in dom{f}，t > 0\}.若 f 是凸函数,则 g 是凸函数$