题目链接:洛谷1268.
—————————————-
概述
题目大意如下.
给你一棵有
n
个叶子节点的树,并告诉你每个叶子节点到其他叶子节点之间的距离,让你还原这棵树,输出边权之和.(
—————————————-
分析
第一眼看到题: “WTF? 构造? 我最虚的就是构造了..”
之后画图分析,发现了一个自认为正确的构造算法,在讲正解之前我先口胡一下.
口胡构造法
我们观察一下题目样例提供的表:

我们只看表的前两行,也就是节点1和节点2到其他点的距离,有没有发现什么特殊的地方?
没错! 假如我们不看前两列, 那么后面3列的数的差值都一样! 那么对应到图上, 节点1和节点2的关系正好是同一个节点的两个儿子.
经过一番简单的演绎与推理之后,我得到了初步结论: 对于同一节点的2个儿子, 他们到其它点
u
的距离的差值都相等. 公式化一点就是: 设这两个儿子分别是
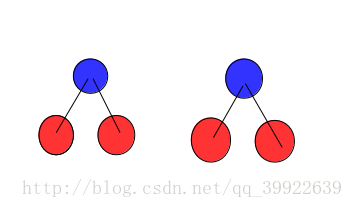
那么知道这个之后, 我们可以暴力枚举每一个点对 x,y , 判断他们是否是同一个节点的儿子. 之后我们得到如下图所示的关系图:
图中红色节点为叶子节点, 紫色节点为它的父亲节点. 我们把所有红色节点与紫色节点之间的边权记入答案.(边权可以在判断是否属于同一紫色节点的儿子时计算出来) 同时,把各个红色节点从图中删除, 把紫色节点当做新的红色节点继续重复这个操作. 至于紫色节点之间的距离, 我们可以通过红色节点之间的距离算出来.
这个算法的复杂度为 O(n3logn) , 正确性我不清楚, 反正我找不出反例来证明它是错的. 不过由于只是口胡, 我并没有尝试写代码. 假如有热心读者找出了这个做法的漏洞或者码出了我上面的做法, 欢迎骚扰 !
标准做法
我们令
g(x,y)
表示点
x
到点
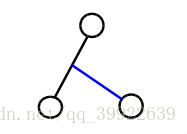
我们先考虑 n=2 的时候,
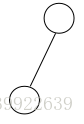
此时答案显然是
g(1,2).
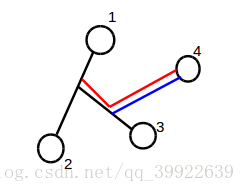
现在考虑 n=3 , 那么第三个点显然是 g(1,2) 的一个分支, 如下图:
我们设分支长度为 len , 那么答案就是 g(1,2)+len. 我们可以发现, len=g(1,3)+g(2,3)−g(1,2)2.
那么, 对于 n>3 的情况也同理, 如下图:
我们记 len 为第四个点的分支长度, 那么此时的答案即是3个点时候的答案加上 len .
对于上图, 第四个点既在 g(1,2) 的分支上(红色线段), 也在 g(1,3) 的分支上(蓝色线段). 如果我们认为第四个节点是 g(1,2) 的分支, 那么答案就会多算中间的那一小段, 所以只有认为第四个点是 g(1,3) 的分支时才能加上正确答案.
所以, 我们枚举
1
~
时间复杂度 O(n2).
—————————————-
代码
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#define ll long long
#define For(i, j, k) for(int i = j; i <= (int)k; ++ i)
#define Forr(i, j, k) for(int i = j; i >= (int)k; -- i)
#define INF 1 << 30
using namespace std;
const int maxn = 30 + 5;
int n, Ans;
int d[maxn][maxn];
inline int Read(){
int x = 0; char c = getchar();
for(; !isdigit(c); c = getchar());
for(; isdigit(c); c = getchar()) x = (x << 3) + (x << 1) + (c ^ 48);
return x;
}
inline void chkmin(int &x, int y){
if(y < x) x = y;
}
int main(){
while(1){
n = Read();
if(!n) break;
For(i, 1, n - 1)
For(j, i + 1, n)
d[i][j] = d[j][i] = Read();
Ans = d[1][2];
For(i, 3, n){
int t = INF;
For(j, 2, i - 1)
chkmin(t, (d[1][i]+d[j][i]-d[1][j])/2);//计算最小的分支长度
Ans += t;
}
printf("%d\n", Ans);
}
return 0;
}—————————————-
小结
这道题说实话并不是很难, 但是思维强度比较高, 很考验OIer对树这个结构的理解. 我开发的那个口胡构造法虽然后来也过了, 但是相比标算还是逊色了不少. 以后还是要多发散思维, 多练练这种思考题比较好.
—————————————-
——wrote by miraclejzd.








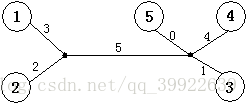
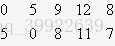














 859
859

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








