如何证明弹簧振子的震动周期与初始位置无关

如下图所示的一个与弹簧相连的小球，小球称为振子，弹簧的质量被忽略。弹簧的另一端与墙体相连。弹簧和振子都放在光滑（即摩擦力忽略不计）的水平平面上，弹簧处于松弛状态（既不拉伸也不压缩）。

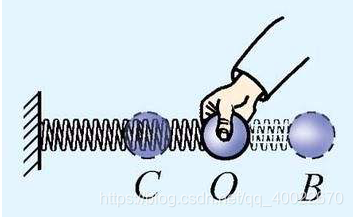
现在把振子拉倒B点，然后松手，振子被弹簧拉扯，速度逐渐加快，直到经过O点。之后振子依靠惯性挤压弹簧，速度逐渐变慢到达C点后为零。之后振子就会在B、C之间来回振动。|BO| = |CO|成立。

假设振子的质量是m（千克），弹簧的弹性系数是k（牛顿/米），|BO|的长度等于c，我们的问题是：请用微积分的办法给出振子速度v和时间t之间的关系，并说明：无论振子的初始位置在哪里，其振动周期都是相同的。也就是说震动周期与振子的初始位置无关。这个性质经常被用来制作手表等计时工具。

解答

 说明

振子在任意时刻受到的弹簧的力f都与它和O点之间的位移s成正比，所以有：

根据牛顿第三运动定律，，其中a是加速度。于是有：

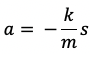
加速度a是速度v对时间t的导数，v是位移s对时间的导数。对上式等号两边分别求导，得：

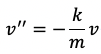
这是一个二阶微分方程，且v的系数小于0，所以有：

                 （1）

其中b是一个常数。我们待会求解它。先看看振子经过O时的速度，显然此时振子的速度的绝对值最大。而上式中只有当：

时速度的绝对值最大。所以上式就是振子从B运动到O的时间，是振子来回振动的1/4周期，所以，弹簧振子的震动周期：

由于这个时间与振子的初始位置即c无关，所以无论振子的初始位置在哪里，其振动周期都是相同的。

现在来推导常数b。由于速度v相对于时间t的积分等于位移，所以有：

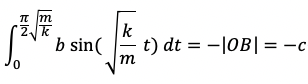
 所以有： 

所以：

代入速度公式(1)中，得：