矩阵分析与应用(23)

最新推荐文章于 2024-06-13 20:02:58 发布

Butterfffly

最新推荐文章于 2024-06-13 20:02:58 发布

阅读量519

点赞数

分类专栏：矩阵分析与应用文章标签：矩阵

本文链接：https://blog.csdn.net/qq_40206924/article/details/126352450

版权

矩阵分析与应用专栏收录该内容

22 篇文章 7 订阅

订阅专栏

学习来源：《矩阵分析与应用》张贤达清华大学出版社

矩阵求导

一、标量、向量、矩阵和函数

对于一个函数

$function(input)$

根据函数 $function$ 和自变量 $input$ 的不同类型可以将函数 $f(x)$ 分为不同的种类。

1. 函数为标量

$function$ 为实值标量函数，用 $\bar{f}$ 表示。

1.1 自变量为标量

函数的自变量是标量，用 $\bar{x}$ 表示。如：

$\bar{f}(\bar{x})=\bar{x}+1$

1.2 自变量为向量

函数的自变量是向量，用 $x$ 表示。如：

$x=[x_1,x_2,x_3]^T$

$\bar{f}(x)=a_1x_1^2+a_2x_2^2+a_3x_3^2+a_4x_1x_2$

1.3 自变量为矩阵

函数的自变量是矩阵，用 $X$ 表示。如：

$X=\begin{bmatrix} x_{11} &x_{12} \\ x_{21} & x_{22} \end{bmatrix}$

$\bar{f}(X)=a_1x_{11}^2+a_2x_{12}^2+a_3x_{21}^2+a_4x_{22}^2$

2. 函数为向量

$function$ 为向量函数，用 $f$ 表示。

2.1 自变量为标量

$f_{3\times 1}(\bar{x})=\begin{bmatrix} f_1(\bar{x})\\ f_2(\bar{x}) \\ f_3(\bar{x}) \end{bmatrix}=\begin{bmatrix} \bar{x}+1\\ 2\bar{x}+1 \\ 3\bar{x}+1 \end{bmatrix}$

2.2 自变量为向量

$x=[x_1,x_2,x_3]^T$

$f_{3\times 1}(x)=\begin{bmatrix} f_1(x)\\ f_2(x) \\ f_3(x) \end{bmatrix}=\begin{bmatrix} x_1+x_2+x_3\\x_1+2x_2+3x_3 \\ x_1^2+x_2^2+x_3^2 \end{bmatrix}$

2.3 自变量为矩阵

$X=\begin{bmatrix} x_{11} &x_{12} \\ x_{21} & x_{22} \end{bmatrix}$

$f_{3\times 1}(X)=\begin{bmatrix} f_1(X)\\ f_2(X) \\ f_3(X) \end{bmatrix}=\begin{bmatrix} x_{11}+x_{12}+x_{x_21}+x_{22}\\ x_{11}x_{12}+x_{21}x_{22}+x_{12}x_{21} \\ 2x_{11}+3x_{22}+4x_{12} \end{bmatrix}$

3. 函数为矩阵

$function$ 为矩阵函数，用 $F$ 表示。

3.1 自变量为标量

$F_{3\times 2}(\bar{x})=\begin{bmatrix} f_{11}(\bar{x}) &f_{12}(\bar{x}) \\ f_{21}(\bar{x}) &f_{22}(\bar{x}) \\ f_{31}(\bar{x}) & f_{32}(\bar{x}) \end{bmatrix}=\begin{bmatrix} \bar{x}+1 &\bar{x}+2 \\ \bar{x}^2+1 & \bar{x}^2+2\\ \bar{x}^3+1 & \bar{x}^3+2 \end{bmatrix}$

3.2 自变量为向量

$x=[x_1,x_2,x_3]^T$

$F_{3\times 2}(x)=\begin{bmatrix} f_{11}(x) &f_{12}(x) \\ f_{21}(x) &f_{22}(x) \\ f_{31}(x) & f_{32}(x) \end{bmatrix}=\begin{bmatrix} x_1+x_2+x_3 +1&x_1+x_2+x_3+2 \\ x_1^2+x_2+x_3 & x_1+x_2^2+x_3^2\\ x_1+2x_2+3x_3 & 3x_1+2x_2+x_3 \end{bmatrix}$

3.3 自变量为矩阵

$F_{3\times 2}(X)=\begin{bmatrix} f_{11}(X) &f_{12}(X) \\ f_{21}(X) &f_{22}(X) \\ f_{31}(X) & f_{32}(X) \end{bmatrix}=\begin{bmatrix} x_{11}+x_{12}+x_{21} +1&x_{12}+x_{21}+x_{22}+2 \\ 2x_{11}+3x_{12}+4x_{21} +2 & 3x_{11}+4x_{12}+5x_{21} +3\\ 7x_{11}+x_{12}+4x_{21} & x_{11}+5x_{12}+x_{21} +2\end{bmatrix}$

二、求导

求导的本质就是函数 $function$ 中的每个 $f$ 分别对自变量中的每个元素求偏导，最终将结果写成向量、矩阵的形式。

例如：有

$x=[x_1,x_2,x_3]^T$

$\bar{f} (x)=x_1^2+x_1x_2+x_2x_3$

列向量形式的求导结果：

$\frac{\partial \bar{f} (x)}{\partial x_{3\times 1}}=\begin{bmatrix} \frac{\partial \bar{f}}{\partial x_1}\\ \frac{\partial \bar{f}}{\partial x_2} \\ \frac{\partial \bar{f}}{\partial x_3} \end{bmatrix}=\begin{bmatrix} 2x_1+x_2\\ x_1+x_3 \\ x_2 \end{bmatrix}$

以行向量的形式展开：

$\frac{\partial\bar{f} (x)}{\partial x_{3\times 1}^T}=\left [ \frac{\partial \bar{f}}{\partial x_1},\frac{\partial \bar{f}}{\partial x_2},\frac{\partial \bar{f}}{\partial x_3} \right ]=\left [ 2x_1+x_2,x_1+x_3,x_2 \right ]$

因此，若函数 $function$ 有 $m$ 个 $f$ ，自变量 $input$ 有 $n$ 个元素，则求导后有 $m\times n$ 个结果，这 $m\times n$ 个结果可以按行向量排列、列向量排列或以矩阵形式排列。

三、矩阵求导结果的布局

1. 自变量为向量 $x=[x_1,x_2,\cdots ,x_n]^T$ 的实值函数 $\bar{f} (x)$

1.1 行向量偏导形式：

$D_x\bar{f} (x)=\frac{\partial\bar{f} (x)}{\partial x^T}=\left [ \frac{\partial \bar{f}}{\partial x_1} ,\frac{\partial \bar{f}}{\partial x_2},\cdots ,\frac{\partial \bar{f}}{\partial x_n}\right ]$

1.2 列向量偏导形式（梯度向量形式）：

$\bigtriangledown _x\bar{f} (x)=\frac{\partial \bar{f}(x)}{\partial x^T}=\left [ \frac{\partial \bar{f}}{\partial x_1}, \frac{\partial\bar{f}}{\partial x_2},\cdots , \frac{\partial \bar{f}}{\partial x_n} \right ]^T$

与 $D_x\bar{f}(x)$ 互为转置。

2. 自变量为矩阵 $X_{m\times n}=(x_ij)_{i=1,j=1}^{m,n}$ 的实值函数 $f(X)$

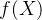
2.1 行向量偏导形式

先把矩阵 $X$ 按列划分转化为一个个列向量，再按顺序组成一个列向量，即：

$vec(X)=\left [ x_{11},x{21},\cdots ,x_{m1},x_{m2},\cdots ,x_{1n},x_{2n},\cdots ,x_{mn} \right ]^T$

然后按照函数为标量函数，自变量为向量的形式求导，得到：

$D_{vec_X}\bar{f}(X)=\frac{\partial \bar{f} (X)}{\partial vec^T(X)}=\left [ \frac{\partial \bar{f}}{\partial x_{11}},\frac{\partial \bar{f}}{\partial x_{21}} ,\cdots ,\frac{\partial \bar{f}}{\partial x_{m1}},\frac{\partial \bar{f}}{\partial x_{12}},\cdots ,\frac{\partial \bar{f}}{\partial x_{m2}},\cdots ,\frac{\partial \bar{f}}{\partial x_{1n}},\frac{\partial \bar{f}}{\partial x_{mn}}\right ]$

2.2 Jacobian 矩阵形式

先把自变量 $X$ 转置，再对转置后的每个位置的元素求偏导，结果布局与 $X$ 转置后的布局一致。

$D_X\bar{f} (X)=\frac{\partial \bar{f}(X)}{\partial X_{m\times n}^T}=\begin{bmatrix} \frac{\partial \bar{f}}{\partial x_{11}} & \frac{\partial \bar{f}}{\partial x_{21}} &\cdots & \frac{\partial \bar{f}}{\partial x_{m1}} \\ \frac{\partial \bar{f}}{\partial x_{12}} & \frac{\partial \bar{f}}{\partial x_{22}} &\cdots & \frac{\partial \bar{f}}{\partial x_{m2}} \\ \vdots & \vdots & &\vdots \\ \frac{\partial \bar{f}}{\partial x_{1n}} & \frac{\partial \bar{f}}{\partial x_{2n}} &\cdots & \frac{\partial \bar{f}}{\partial x_{mn}} \end{bmatrix}_{n\times m}$

2.3 列向量偏导形式（梯度向量形式）

先把自变量 $X$ 按 2.1 中的操作列向量化，再按 1.2 的式子进行求导：

$\bigtriangledown _{vec_X}\bar{f}(X)=\frac{\partial \bar{f} (X)}{\partial vec(X)}=\left [ \frac{\partial \bar{f}}{\partial x_{11}},\frac{\partial \bar{f}}{\partial x_{21}} ,\cdots ,\frac{\partial \bar{f}}{\partial x_{m1}},\frac{\partial \bar{f}}{\partial x_{12}},\cdots ,\frac{\partial \bar{f}}{\partial x_{m2}},\cdots ,\frac{\partial \bar{f}}{\partial x_{1n}},\frac{\partial \bar{f}}{\partial x_{mn}}\right ]^T$

2.4 梯度矩阵形式

直接对自变量 $X$ 的每个位置的元素逐个求偏导，结果布局与 $X$ 的布局一致。

$\bigtriangledown _X\bar{f} (X)=\frac{\partial \bar{f}(X)}{\partial X_{m\times n}}=\begin{bmatrix} \frac{\partial \bar{f}}{\partial x_{11}} & \frac{\partial \bar{f}}{\partial x_{12}} &\cdots & \frac{\partial \bar{f}}{\partial x_{1n}} \\ \frac{\partial \bar{f}}{\partial x_{21}} & \frac{\partial \bar{f}}{\partial x_{22}} &\cdots & \frac{\partial \bar{f}}{\partial x_{2n}} \\ \vdots & \vdots & &\vdots \\ \frac{\partial \bar{f}}{\partial x_{m1}} & \frac{\partial \bar{f}}{\partial x_{m2}} &\cdots & \frac{\partial \bar{f}}{\partial x_{mn}} \end{bmatrix}_{m\times n}$