高级搜索树之红黑树

1、前言

对于大部分人来讲，红黑树绝对是一个“高级”的代名词，很多人不了解红黑树，也不知道它能做什么。

实际上，完全不需要这样想，红黑树并没有大家想象的那么深奥。

​

当然，学习红黑树并不是没有前提条件的，首先你需要了解 AVL 树，其次还需要对 B 树有一定程度的认识，在这个基础之上，相信你一定能掌握好红黑树！

2、简介

平衡二叉树（BBST）的形式多样，且都有各自的特色！例如有 AVL ，伸展树，B-树（可以简单的认为是 BBST 一种）

但是要明确一点的是，无论什么样的 BBST，或者说无论什么样的数据结构被人们所发现出来，都是为了解决实际问题的！

因此，学习红黑树之前要明白它是要解决什么问题才被创造出来的，带着这个目标再去学习会事半功倍。

2.1、来历

有这样一个问题，即我们需要对某个数据组织进行历史版本的保存与访问，那么在一开始，想要实现支持对历史版本的访问，就只能单独存放每一个版本，就像这样：

然而你会发现，随着版本的不断增加，越来越多的重复数据被存放，而每个版本的新增复杂度为 O(logh + logn)。累计达到 O(h*n) 。

注：每个版本新增的复杂度表示树的拓扑结构改变量

这样的存放方式显然并不友好，因此我们该如何进行优化呢？没错，利用版本之间的关联性！

通过大量的共享，少量更新的方式，可以实现每个版本的新增复杂度仅为 O(logn)：

在上面的优化中，每个版本新增的复杂度从 O(logh + logn) 优化到了 O(logn)。

那么能否实现每个版本新增的复杂度为 O(1) 呢？

遗憾的是，AVL ，伸展树等 BBST 均不能实现这一目标！

例如在 AVL 中，尽管可以保证最坏情况下的单词操作速度，但需要额外嵌入平衡因子等标识；更重要的是，AVL 的删除操作之后的重平衡可能需要做多达 Ω(logn)次旋转，这意味全树整体拓扑结构的大幅度变化！

因此我们需要一种新的数据结构，能在插入删除的情况下保证全树拓扑结构的更新仅涉及常数个节点，即达到期望的 O(1) 复杂度。

红黑树就是在这样的情况下出现了！

2.2、定义

前提：为了便于对红黑树的理解，实现与分析，我们统一的引入“外部节点”的概念，当然，这些外部节点的引入只是假想式的，在具体实现时并不一定需要兑现为真实的节点。

定义：由红、黑两色节点组成的二叉搜索树若满足以下条件，即为红黑树：

1）树根始终为黑色

2）外部节点均为黑色

3）其余节点若为红色，则其孩子节点必为黑色

4）从任一外部节点到根节点的沿途，黑节点的数目相等

第一点很好保证，第二点在我们引入了外部节点之后也很容易理解，第四点只需要注意一条完整路径中的黑节点数量要统一即可。

第三点：红节点的父节点一定是黑色的，其孩子也一定为黑色，即红节点不能相邻排列。

黑深度：除去根节点本身，沿途所经黑节点的总数称作该节点的黑深度，而根节点的黑深度为 0

黑高度：除去（黑色）外部节点，沿途所经黑节点的总数称作该节点的黑高度，所有外部节点的黑高度均为 0

特别地，根节点的黑高度亦称作全树的黑高度，在数值上与外部节点的黑深度相等。

2.3、理解

相信在阅读完上面的定义之后，大部分同学仍然会觉得困惑。实际上但从上面的定义来看确实比较晦涩难懂。但幸运的是如果你已经学习了 B-树，那么在经过适当的转换之后，红黑树和一颗 4 阶 B-树相互等价！

因此我们可以借助 B-树来帮助我们理解红黑树。

转换规则：将黑节点与其红孩子视作（关键码合并）超级节点！

那么无非下面四种组合：

注：指向黑节点用实线，而指向红节点用虚线。

平衡性：由等价性，既然 B-树 是平衡的，红黑树自然也是平衡的。

红黑树的黑高度不低树高度的一半，反之，树高度不超过黑高度的两倍。（ h < 2H ）

也就是说，尽管红黑树不能如完全树那样可做到理想平衡，也不如 AVL 树那样可做到较严格的适度平衡，但其高度仍控制在最小高度的两倍以内，从渐进的角度看仍是 O(logn)，依然保证了适度平衡 --- 这正是红黑树可高效率支持各种操作的基础。

3、实现

首先给出红黑树的模板类：

template <typename T> class RedBlack: public BST<T> {    protected:        void solveDoubleRed( BinBodePosi(T) x ); // 双红修正        void solveDoubleBlack( BinBodePosi(T) x ); // 双黑修正        int updateHeight( BinBodePosi(T) x ); // 更新节点 x 的高度​    public:        // search 与 BST 中的 search 完全一致，可沿用        BinNodePosi(T) insert( const T & e ); // 插入（重写）        bool remove( const T & e ); // 删除（重写）}

关于其中更新高度方法，是因为在红黑树中，只关注黑节点的高度：

template <typename T>int RedBlack<T>::updateHeight ( BinBodePosi(T) x ) {    // 取左右子树中最大的高度    x -> height = max( stature( x -> lc ), stature( x -> rc ) );    if ( IsBlack( x ) ) {        x -> height++; // 如果当前节点是黑节点，则高度加 1    }    return x -> height;}

3.1、insert

算法思路：

1）调用 search 方法判断目标节点是否存在，若存在则直接返回；

2）若不存在，则按 BST 常规插入节点，此时目标节点一定为末端节点；

3）将 x 染红（除非是根，染成黑色）；

4）经过上面三步，红黑树定义的第 1，2，4 点都满足，但是第 3 点却不一定，可能会出现“双红”问题，那么必须做“双红修正”；

5）修正完毕后，返回插入的节点。

接下来，我们就根据思路来实现具体的代码：

template <typename T>BinNodePosi(T) RedBlack::insert( const T & e ) {​    // 搜索目标节点 e 是否存在    BinNodePosi(T) & x = search( e );    // 若存在，则直接返回    if ( x ) {        return x;    }​    // 创建红节点，以 _hot 为父节点，黑高度为 -1    x = new BinNode<T>( e, _hot, NULL, NULL, -1 );​    // 如果有必须则做“双红修正”    solveDoubleRed( x );​    // 返回插入的节点    return x ? x : _hot -> parent;} // 无论 e 是否存在于原树中，返回时总有 x -> data == e

从上面代码实际可以看出，本身的插入操作并不难理解和实现，关键就在于插入的行为有可能导致红黑树的合法定义被破坏，即出现“双红问题”。此时就需要进行“双红修正”，在上述代码中，通过 solveDoubleRed 方法实现。

3.2、solveDoubleRed

首先来看看不需要调整的情况：

template <typename T>void RedBlack<T>::solveDoubleRed ( BinNodePosi(T) x ) {​    // 如果 x 是作为根节点插入一颗空树的情况    if ( IsRoot( *x ) ) {        _root -> color = RB_BLACK; // 根节点必为黑色        _root -> height++;        return; // 直接返回    }​    // 考察 x 的父亲 p （必存在，因为根节点情况已经排除）    BinNodePosi(T) p = x -> parent;    if ( IsBlack( p ) ) {        // 若 p 为黑，则可以退出，因为插入的 x 为红，此时不会出现双红问题        return;     }​    /**     * x 的祖父必存在，因为上面排除了 x 为根，和 x 的父亲 p 为黑的情况     * 则此时 p 就一定是红色，则 p 就不可能为根节点，因此 p 上面一定有其他黑色节点     */     BinNodePosi(T) g = p -> parent; // x 的祖父 g 必存在且必为黑​    // 获取 x 的叔父节点，并根据 u 的颜色进行分别处理    BinNodePosi(T) u = uncle( x );​    if ( IsBlack( p ) ) {        /* u 为黑色时，或者 u 为 NULL 时 */    } else {        /* u 为红色时 */    }}

在双红修正过程中，有两种情况要分开讨论，即插入节点 x 的叔父节点 u 的颜色：

1、RR-1：叔父节点 u 的颜色为黑色时

下面给出两种情况，另外两种的完全对称：

我们前面提到过，红黑树经过适当的变换，和 4 阶的 B-树对等，那么我们将该红黑树调整下，使之用 B-树的形式表示，就像这样：

发现了吗，x、p、g 的顺序中序遍历的顺序排列！

那实际上，我们完全可以参照 AVL 树的算法，在 (a)，(b)中做局部的 3+4 重构，即将节点 x、p、g 及其四颗子树，按中序遍历的顺序重新组合为：

b 转黑，a 或 c 转红

此时你会发现，改变之后的 B-树 局部的拓扑结构并没有发生改变！

可以看到当我们在将红黑树按中序遍历的顺序转换成 B-树 形式时，它是不是就正好是上面提到的 AVL 树种的 3+4 重构的结果呢！

即 (a`) (b`) (c`) 的红黑树结构不同，但是 B-树的结构一致！而从 (a`) (b`) 的结构调整到 (c`) 的结构，也不过经过一两次旋转！

这也就是为什么在这种情况下，红黑树的拓扑结构改变量在常数次。然后再通过两次染色，就可以实现双休修正了！

而对于红黑树而言，也仅需要通过 一两次 旋转 加上两次染色即可实现双休修正！

来看一下代码实现：

template <typename T>void RedBlack<T>::solveDoubleRed ( BinNodePosi(T) x ) {​     /* ...... */​    /* u 为黑色时，或者 u 为 NULL 时 */    if ( IsBlack( p ) ) {                /**         * 若 x 是 p 的左孩子，则 p 由红转黑，x 保持红；         * 若 x 是 p 的右孩子，则 x 由红转黑，p 保持红         * g 一定由黑色转为红色         */        if ( IsLChild( *x ) == IsLChild( *p ) ) {            p -> color = RB_BLACK;        } else {            x -> color = RB_BLACK;        }        g -> color = RB_RED;​        // 旋转调整操作！        BinNodePosi(T) gg = g -> parent;        BinNodePosi(T) r = FromParentTo( *g ) = rotateAt( x );​        // 调整之后的新子树，需要与原曾祖父连接        r -> parent = gg;            } else {        /* u 为红色时 */    }}

2、RR-2：叔父节点 u 的颜色为红色时

此时在等价的 B-树 中等效于超级节点发生上溢！

以下给出两种情况，另外两种完全对称：

此时我们可以参照 B-树 解决上溢的方法（分裂）来进行处理，就像这样：

从上面的 b 到 c，分析时我们是按照 B-树 的分裂操作从 1 -> 3 逐步调整的。

 

而最后的结果你会发现，从 b 到 c 只不过是 p、u 的颜色转为黑，g 的颜色转为红而已！而局部的拓扑结构并没有发生任何改变。

而相信此时的你也可能已经发现，既然时分裂，就有可能继续向上传递，则可能导致 g 与其父节点再次构成双红问题。

幸运的是，就算出现这样的情况，也只不过再重复修正操作而已，而最坏的情况也不过到达树根就会停止。

注：如果上溢真的到达了树根，则需要将树根节点强行转为黑色，并且整树的黑高度需要加1.

接下来让我们看看具体的代码实现：

template <typename T>void RedBlack<T>::solveDoubleRed ( BinNodePosi(T) x ) {​     /* ...... */​    if ( IsBlack( p ) ) {                /* u 为黑色时，或者 u 为 NULL 时 */            } else { /* u 为红色时 */        p -> color = RB_BLACK; p -> height ++; // p由红转黑        u -> color = RB_BLACK; u -> height ++; // u由红转黑        if ( !IsRoot( *g ) ) {             g -> color = RB_RED; // g若非根，则转红        }        solveDoubleRed ( g ); // 继续调整g    }}​

3、小结

在插入操作过程中，有可能会发生双红的非法现象。

而通过“双红修正”我们可以在常数时间内实现修正！

可以来看看这一份流程图，正是我们前面详解过的方案：

而在每一次插入时，红黑树都可以在 O(logn) 时间内完成！

其中至多做：

1）O(logn) 次节点染色

2）一次 “3+4”重构

表明插入操作的拓扑结构改变量为 O(1) ！

3.3、remove

算法思路：

1）调用 search 方法判断目标节点是否存在，若不存在则直接返回；

2）按照 BST 常规算法，执行 removeAt 操作删除目标节点 x ；

3）根据 removeAt 语义，如果返回 r ，则表示 x 由孩子 r 接替；

4）经过上面三步，虽然第 1、2 步依然满足，但 3、4 步却不一定能保证；

5）依据情况进行修正

注意，有一种情况较好处理，即 x（被删除节点） 与 r（替代 x 的节点） 中有一个为红节点，则在删除 x 后，只需要把 r 染黑即可：

先来看一下 remove 算法：

template <typename T>bool RedBlack<T>::remove( const T & e ) {​    // 搜索目标节点是否存在，若不存在则直接返回 false    BinNodePosi(T) & x = search( e );    if ( !x ) {        return false;    }​    // 删除 _hot 的某孩子，r 指向其接替者    BinNodePosi(T) r = removeAt( x, _hot );​    // 若删除后为空树，则可直接返回true    if ( !(--_size) ) {        return true;    }​    // 若被删除的是根，则将新根置黑，并跟新全树高度    if ( !_hot ) {        _root -> color = RB_BLACK;        updateHeight( _root );        return true;    }​    // 到了这里，接下来的情况中，x 一定不是根节点​    // 若父亲（及祖先）依然平衡，则无需调整    if ( BlackHeightUpdated( *_hot ) ) {        return true;    }​    // 至此，以下情况必失衡​    // 1、若替代节点 r 为红，则只需简单的将其置黑即可    if ( IsRed( r ) ) {        r -> color = RB_BLACK;        r -> height++;        return true;    }​    // 2、若 r 及其被替代节点 x 均为黑色，则此时出现 “双黑问题”！    solveDoubleBlack( r ); // 双黑修正​    return true;}​

接下来，我们就要针对双黑问题出现进行修正！

3.4、solveDoubleBlack

如果 x 与 r 均为黑色节点，则存在“双黑问题”：

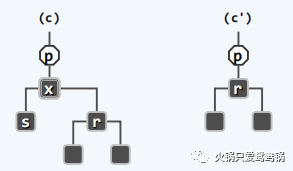
在摘除 x 并替换成 r 之后，全树的 黑深度 不再统一，而对应的 B-树 结构中 x 所属的节点发生下溢。

因此，在新树中（删除x之后的树），需要考察两个节点：

1）r 的父亲节点 p = r -> parent，这也是原树中 x 的父亲

2）r 的兄弟节点 s = ( r == p -> lc ) ? p -> rc : p -> lc

则就要分四种情况考虑!

先来看算法整体框架：

template <typename T>void RedBlack<T>::solveDoubleBlack( BinNodePosi(T) r ) {​    // 要求 r 的父亲 p 必须存在    BinNodePosi(T) p = r ? r -> parent : _hot;    if ( !p ) {        return;    }​    // 获取 r 的兄弟节点 s    BinNodePosi(T) s = ( r == p -> lc ) ? p -> rc : p -> lc;​    // 以下分为四种情况，分别进行讨论！​    /* 兄弟 s 为黑 */    if ( IsBlack( s ) ) {​        BinNodePosi(T) t = NULL; // 以下将 t 去做 s 的红孩子                // 如果 s 的左孩子存在，且左孩子为红        if ( HasLChild( *S ) && IsRed( s -> lc ) ) {            t -> s -> lc;        } else {            t = s -> rc;        }​        if ( t ) {            /* 情况一：黑 s 有至少一个红孩子（ BB-1 ） */        } else {            /* 情况二：黑 s 无红孩子，p 为红（ BB-2R ） */            /* 情况三：黑 s 无红孩子，p 为黑（ BB-2B ） */        }​    } else {        /* 情况四：兄弟 s 为红（ BB-3 ） */    }​}

1、情况一：黑 s 有至少一个红孩子（ BB-1 ）

如果是此种情况，则可以采用 3 + 4 重构，t、s、p 重命名为 a、b、c ，具体的过程不再赘述，前面已经多次提到。

然后对颜色进行调整：r  保持黑，a 和 c 染黑，b 继承 p 的原色！

如此，则红黑树的合法定义再全局得以恢复 --- 删除完成！

图中只是给出了一种情况，还有 s 的右孩子为红，或者两个孩子都为红的情况，与此处类似！

而在对应的等效 B-树 中，则表示为通过关键码的旋转来解决超级节点的下溢问题，就像这样：

那么再来看看具体实现吧：

template <typename T>void RedBlack<T>::solveDoubleBlack( BinNodePosi(T) r ) {​    /* ...... */​    /* 兄弟 s 为黑 */    if ( IsBlack( s ) ) {​        /* ...... */​        /* 情况一：黑 s 有红孩子（ BB-1 ） */        if ( t ) {                        RBColor oldColor = p -> color; // 备份 p 的颜色​            // 3+4 旋转操作，b 为新的父节点            BinNodePosi(T) b = FromParentTo( *p ) = rotateAt( t ); ​            // 将新子树的左右孩子颜色都染黑            if ( HasLChild( *b ) ) b -> lChild -> color = RB_BLACK;            if ( HasLChild( *b ) ) b -> rChild -> color = RB_BLACK;​            // 新的父节点 b 继承原 p 节点的颜色            b -> color = oldColor;​            // 更新高度            updateHeight( b -> lc );            updateHeight( b -> rc );            updateHeight( b );​        } else {            /* 情况二：黑 s 无红孩子，p 为红（ BB-2R ） */            /* 情况三：黑 s 无红孩子，p 为黑（ BB-2B ） */        }​    } else {        /* 情况四：兄弟 s 为红（ BB-3 ） */    }​}

2、情况二：黑 s 无红孩子，p 为红（ BB-2R ）

可以看到，从 (a) 到 (b) 虽然我们通过对应的 B-树的形式取曲折理解，即该修正过程等效于 B-树 中下溢节点与兄弟合并。

但是实际上的结果却仅仅只是颜色的改变：r 保持黑，s 转红，p 转黑！

此时红黑树合法定义在全局得以恢复！且可以看到虽然 B-树 失去了关键码 p，但是这种情况下上层节点不会继续发生下溢，则表明修正完成！

3、情况三：黑 s 无红孩子，p 为黑（ BB-2B ）

在情况三中，通过对应 B-树 会发现，虽然下溢节点与兄弟合并能解决局部问题，但是必会导致上层节点发生下溢（因为 p 和 s 都对应于单关键码节点）。

幸运的是，这种情况仍然可以继续分情况处理，而即使下溢会向上传递，而最多也就是到达树根，至多 O(logn) 。

实际上的结果却仅仅只是颜色的改变：s 转红，r 与 p 保持黑！

接下来一起看一下情况二与情况三的代码实现：

template <typename T>void RedBlack<T>::solveDoubleBlack( BinNodePosi(T) r ) {​    /* ...... */​    /* 兄弟 s 为黑 */    if ( IsBlack( s ) ) {​        /* ...... */​        if ( t ) {                        /* 情况一：黑 s 有红孩子（ BB-1 ） */​        } else {             /** 情况二：黑 s 无红孩子，p 为红（ BB-2R ）              *  情况三：黑 s 无红孩子，p 为黑（ BB-2B ）              */​            s -> color = RB_RED;            s -> height--;​            // BB-2R：p 转黑，但黑高度保持不变            if ( IsRed( p ) ) {​                p -> color = RB_BLACK;​            } else { // p 保持黑，但黑高度下降，递归修正                 p -> height--;                solveDoubleBlack( p );            }        }​    } else {        /* 情况四：兄弟 s 为红，其他孩子均为黑（ BB-3 ） */    }​}

4、情况四：兄弟 s 为红，其他孩子均为黑（ BB-3 ）

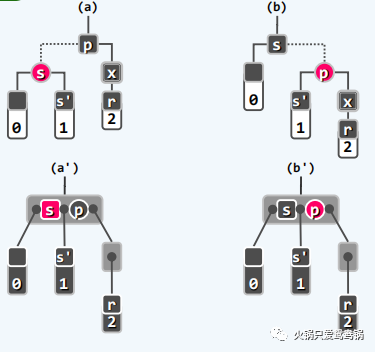
在情况四中，我们没有办法直接来实现修正，而可以通过 zag(p) 或者 zig(p)，然后红 s 转黑，黑 p 转红 进而将情况四转换成 BB-1 或者 BB-2R 的情况！

然后在经过一轮对应的调整即可实现修正，并且保重红黑树的合法定义全局恢复！

来看看具体实现：

template <typename T>void RedBlack<T>::solveDoubleBlack( BinNodePosi(T) r ) {​     /* ...... */​    /* 兄弟 s 为黑 */    if ( IsBlack( s ) ) {​         /* ...... */​        /* 情况一：黑 s 有红孩子（ BB-1 ） */        if ( t ) {                        /* 情况一：黑 s 有红孩子（ BB-1 ） */​        } else {                         /** 情况二：黑 s 无红孩子，p 为红（ BB-2R ）              * 情况三：黑 s 无红孩子，p 为黑（ BB-2B ）              */        }​    } else {  /* 情况四：兄弟 s 为红（ BB-3 ） */               s -> color = RB_BLACK;        p -> color = RB_RED;​        // 取 t 与其父 s 同侧        BinNodePosi(T) t = IsLChild( *s ) ? s -> lc : s -> rc;​        // 对 t 及其父亲，祖父做平衡调整        _hot = P;        FromParentTo( *p ) = rotateAt( t );​        // 继续修正，此时 p 已经转红，故后续只能是 BB-1 或者 BB-2R 的情况        solveDoubleBlack( r );    }​}

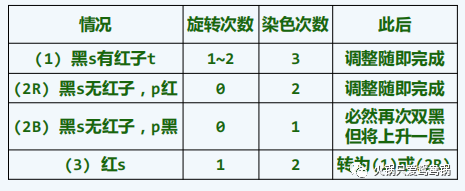
3.5、复杂度分析

红黑树的每一次删除操作，都可在 O(logn) 的时间内完成！

这 O(logn) 时间内最多做：

1）O(logn) 次重染色

2）一次 “ 3+4 ”重构

3）一次单旋

同样，为了便于记忆这里仍然给出一张流程图：

给出操作次数总结图：

至此，红黑树介绍完毕！

最后，欢迎大家关注我的微信公众号：火锅只爱鸳鸯锅！