2022数二真题

选择题

正确答案：B
解析：A选项可以举反例，$y=x^3$在x=0邻域内是单增，但是$y{\prime }_{(0)}=0$
C选项也可以举反例$y=x^4$，则$y\prime =4x^3$,$y\prime \prime =12x^2$
,所以y在x=0邻域内是凹函数，但是$y\prime {\prime }_{(0)}=0$。
选项D而言，因为题目只是说$f(x)$在$x_0$处有二阶导数，病没有说$f(x)$在$x_0$附近也有二阶导数且连续。所以很难说$f(x)$在$x_0$邻域内是凹函数。
而选项B，因为题目说了$f(x)$在$x_0$处有二阶导数，说明$f^{\prime }(x)$在$x_0$邻域内是连续的，又因为选项B里说$f^{\prime }(x_0)>0$,所以在$x_0$的邻域内$f^{\prime }(x)>0$也成立，故而单增。 B选项正确

---

---

正确答案：A
解题思路： 考察积分的审敛法。
首先我们要知道的是${\int }_a^b\frac{1}{(x-a{)}^p}dx$ ，a是瑕点， 且当$p<1$时是收敛的。当$p\ge 1$时是发散的
对于本题来说当$x\to 0^{+}$时，$\frac{lnx}{x^p(1-x{)}^{1-p}}=\frac{lnx}{x^p}$,
$\frac{lnx}{x^p}$的分子可以不看，因为$lnx$的变化速度赶不上$x^p$这种指数级别, 分母是$x^p$,所以当p<1时，积分收敛。
当$x\to 1^{-}$时，$\frac{lnx}{x^p(1-x{)}^{1-p}}=\frac{lnx}{(1-x{)}^{1-p}}=\frac{ln(1+x-1)}{(1-x{)}^{1-p}}=\frac{-1}{(1-x{)}^{-p}}$, 要想让积分收敛，则要让分母中的$-p<1$,即p>-1,
所以本题的答案就出来了。选A

---

---

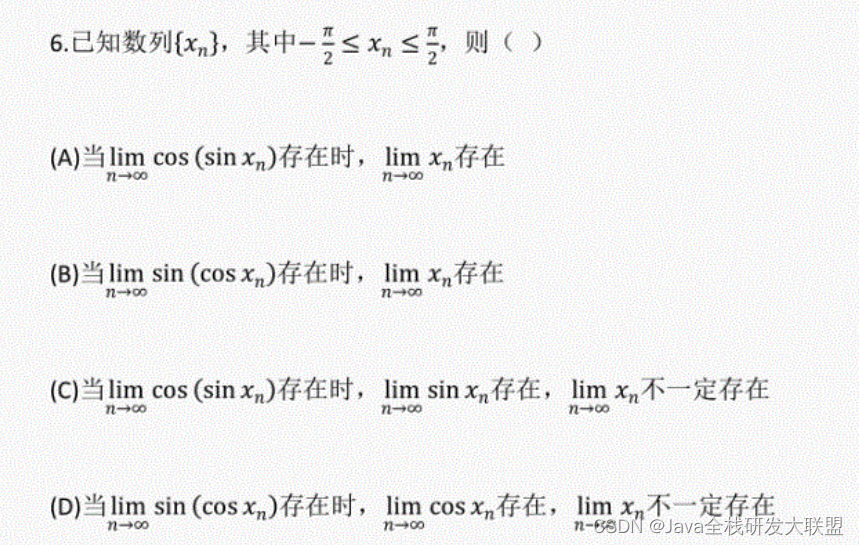
正确答案：D
解题思路:
选项A是错的，我们可以举反例 $x_n=(-1{)}^n\frac{\pi }{2}$， 这个时候${\lim }_{n\to \infty }cos(sin{x}_n)=cos1$
选项B也是错的，反例和A一样,$x_n=(-1{)}^n\frac{\pi }{2}$， 这时${\lim }_{n\to \infty }sin(cos{x}_n)=0$
选型C是错的，反例也是一样，$x_n=(-1{)}^n\frac{\pi }{2}$，这个时候${\lim }_{n\to \infty }cos(sin{x}_n)$存在，而${\lim }_{n\to \infty }sin{x}_n$却不存在。

---

---

正确答案：
解题思路：
先比较$I_1$和$I_2$,主要是比较$\frac{x}{2}$和$ln(1+x)$
不妨设$f(x)=\frac{x}{2}-ln(1+x)$, 则$f^{\prime }(x)=\frac{1}{2}-\frac{1}{1+x}$
,当0<x<1时，$f^{\prime }(x)<0$, 所以$f(x)$单减， 又$f(0)=0$,所以当0<x<1时，$f(x)<0$,即$\frac{x}{2}<ln(1+x)$,所以
$I_1<I_2$,然后就能排除选项B,D, 只能从A和C中选了。
而A和C中重点就是比较$I_2$和$I_3$的大小关系，我们来作差比较
$I_2-I_3=\frac{ln(1+x)}{1+cosx}-\frac{2x}{1+sinx}<\frac{x}{1+cosx}-\frac{2x}{1+sinx}=\frac{2x}{2+2cosx}-\frac{2x}{1+sinx}<0$, (注:当0<x<1时，$2+2cosx>2$,而$1+sinx<2$),所以$I_2<I_3$
(归纳：看到分子里面有$ln(1+x)$，就应该想到$x>ln(1+x)$)

---

---

正确答案: D
解题思路:
判断线性方程组是否有解的问题。 我们首先想到克拉默法则。（注:克莱姆法则判断具有N个方程、N个未知数的线性方程组的解，当方程组的方程个数与未知数的个数不一致时，或者当方程组系数的行列式等于零时，克莱姆法则失效。） 而本题的A矩阵恰好是3阶方阵，可以使用克拉默法则。 判断线性方程组是否有解，还可以看下面的定理。

A矩阵符合范德蒙行列式，所以当我们用克拉默法则的时候，需要算它的行列式的值很简单

第十题

正确答案:C
解题思路:
题目中说了向量组${\alpha }_1,{\alpha }_2,{\alpha }_3$与${\alpha }_1,{\alpha }_2,{\alpha }_4$等价 （注: 等价意味着矩阵秩相同）

解法一：
我们把${\alpha }_1,{\alpha }_2,{\alpha }_3,{\alpha }_4$拼成一个矩阵如下:
① 当$\lambda \ne 1时$
$$\left\{\begin{array}{cccc}\lambda & 1& 1& 1\\ 1& \lambda & 1& \lambda \\ 1& 1& \lambda & {\lambda }^2\end{array}\right\}{=}^{(交换2,3行)}>\left\{\begin{array}{cccc}1& 1& \lambda & {\lambda }^2\\ 1& \lambda & 1& \lambda \\ \lambda & 1& 1& 1\end{array}\right\}$$
$${=}^{(r_2-r_1,r_3-\lambda r_1)}>\left\{\begin{array}{cccc}1& 1& \lambda & {\lambda }^2\\ 0& \lambda -1& 1-\lambda & \lambda -{\lambda }^2\\ 0& 1-\lambda & 1-{\lambda }^2& 1-{\lambda }^3\end{array}\right\}$$
$${=}^{第2行缩小(\lambda -1)倍，第3行缩小(1-\lambda )倍}>\left\{\begin{array}{cccc}1& 1& \lambda & {\lambda }^2\\ 0& 1& -1& -\lambda \\ 0& 1& 1+\lambda & 1+\lambda +{\lambda }^2\end{array}\right\}$$
$${=}^{r_2-r_3}>\left\{\begin{array}{cccc}1& 1& \lambda & {\lambda }^2\\ 0& 1& -1& -\lambda \\ 0& 0& \lambda +2& (1+\lambda {)}^2\end{array}\right\}\text{\hspace{1em}(5)}$$
矩阵(5)的第1,2,3,4列分别对应着${\alpha }_1,{\alpha }_2,{\alpha }_3,{\alpha }_4$
我们发现第3行中的$\lambda +2$和$(1+\lambda {)}^2$不可能同时为0，（注:如果要让$\lambda +2=0$，则$\lambda =-2$,如果让$(1+\lambda {)}^2=0$，则$\lambda =-1$） 所以当$\lambda \ne -1,且\lambda \ne -2$时 ，$r({\alpha }_1,{\alpha }_2,{\alpha }_3)=r({\alpha }_1,{\alpha }_2,{\alpha }_4)=3$

②当$\lambda =1$时，${\alpha }_1,{\alpha }_2,{\alpha }_3,{\alpha }_4$这4个向量都一样，所以$r({\alpha }_1,{\alpha }_2,{\alpha }_3)=r({\alpha }_1,{\alpha }_2,{\alpha }_4)=1$也符合条件。

综上所述， $\lambda \ne -1,且\lambda \ne -2$就是本题的答案

填空题

答案: $y=C_1+e^x(C_{2}cos2x+C_{3}sin2x)$, $C_1,C_2,C_3$是任意常数。
解题思路: 先把对应的特征方程写出来，特征方程是${\lambda }^3-2{\lambda }^2+5\lambda =0$, 方程的解是$\lambda =0或1+2i或1-2i$. 然后看下图二阶常系数微分方程的解， （三阶也是一样的套用这个公式）

对于$\lambda =0,通解y=C_1{e}^0=C_1$,
对于$\lambda =1+2i或1-2i时，通解y=e^x(C_{2}cos2x+C_{3}sin2x)$
然后把两部分通解合并就是最后的答案了

’

大题

解题思路:
题目让我们求$f^{\prime }(1)$,而且题目给的那些条件，很明显让我们用导数定义式来解题
而导数定义式里肯定需要用到$f(1)$,
在${\lim }_{x\to 0}\frac{f(e^{x^2})-3f(1+si{n}^{2}x)}{x^2}=2$中，当$x\to 0$时，分母趋于0，分子是$-2f(1)$,而分子分母的比值是2，所以分子也趋于0。而$f(1)$在x=1处连续，所以$f(1)=0$
然后我们可以把式子改写
${\lim }_{x\to 0}\frac{f(e^{x^2})-f(1)-[3f(1+si{n}^{2}x)-3f(1)]}{x^2}=2$
${\lim }_{x\to 0}\frac{f(e^{x^2})-f(1)}{x^2}-3\frac{f(1+si{n}^{2}x)-f(1)}{x^2}=2$
那怎么计算${\lim }_{x\to 0}\frac{f(e^{x^2})-f(1)}{x^2}$呢？这就是本题的核心了
${\lim }_{x\to 0}\frac{f(e^{x^2})-f(1)}{x^2}={\lim }_{x\to 0}\frac{f(e^{x^2})-f(1)}{e^{x^2}-1}.\frac{e^{x^2}-1}{x^2}=$
${\lim }_{x\to 0}{f}^{\prime }(1).\frac{e^{x^2}-1}{x^2}=f^{\prime }(1)$
然后$-3\frac{f(1+si{n}^{2}x)-f(1)}{x^2}=-3f^{\prime }(1)$
所以整个式子就是 $-2f^{\prime }(1)=2$,所以$f^{\prime }(1)=-1$

---

第18题

解题思路:
本题考察的点很常规，
①一阶非齐次线性微分方程的通解公式 ②弧长公式
对于$2x{y}^{\prime }-4y=2lnx-1$可以转换成$y^{\prime }-\frac{2y}{x}=\frac{2lnx-1}{2x}$, 然后算出通解是
$y=e^{-\int -\frac{2}{x}dx}(\int \frac{2lnx-1}{2x}{e}^{\int -\frac{2}{x}dx}+C)$
$=x^2(\int \frac{2lnx-1}{2x}.-\frac{1}{x^2}dx+C)$
$=x^2(-\int \frac{2lnx}{2x^3}dx+\int \frac{1}{2x^3}dx+C)$
对于$-\int \frac{lnx}{x^3}dx=-\int lnxd(-\frac{1}{2}{x}^{-2})=\frac{1}{2}{x}^{2}lnx-\int \frac{1}{2x^3}dx$
所以整个式子就很好算了，最后得到通解$y=C{x}^2-\frac{lnx}{2}$
然后把$y(1)=\frac{1}{4}$代入，计算出$C=\frac{1}{4}$,所以
$y=\frac{1}{4}{x}^2-\frac{lnx}{2}$ （注:我们顺便把$y^{\prime }=\frac{1}{2}x-\frac{1}{2x}$）
然后开始算曲线弧长，弧长公式是${\int }_a^b\sqrt{1+{y^{\prime }}^2}dx$
本题的曲线弧长=${\int }_1^e\sqrt{1+(\frac{1}{2}x-\frac{1}{2x}{)}^2}dx={\int }_1^e\sqrt{(\frac{1}{2}x+\frac{1}{2x}{)}^2}dx={\int }_1^e(\frac{1}{2}x+\frac{1}{2x})dx=\frac{1}{4}(e^2+1)$

---

解题思路 先把积分区域画出来，如下图所示

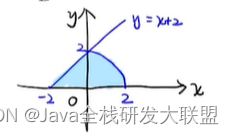
然后我们发现积分函数中有$x^2+y^2$这样的式子，所以我们首先想到用极坐标来求解


解:
(1)题目让我们求$\frac{\partial g(x,y)}{\partial x}$,而$g(x,y)=f(x,y-x)$,所以就相当于求$\frac{\partial f(x,y-x)}{\partial x}$。
而$\frac{\partial f(x,y-x)}{\partial x}=f_1^{\prime }(x,y-x)-f_2^{\prime }(x,y-x)$,这个时候我们刚好可以套用题目中给的条件$\frac{\partial f(u,v)}{\partial u}-\frac{\partial f(u,v)}{\partial v}=2(u-v)e^{-(u+v)};$ 然后就可以推导$f_1^{\prime }(x,y-x)-f_2^{\prime }(x,y-x)=2[x-(y-x))]e^{-[x+(y-x)]}=2(2x-y)e^{-y};$

（2）由$\frac{\partial g(x,y)}{\partial x}=2(2x-y)e^{-y}$，可以得出$g(x,y)=2(x^2-xy)e^{-y}+C(y)$; 又因为第一问里的条件说了$g(x,y)=f(x,y-x)$,所以$f(x,y-x)=g(x,y)=2(x^2-xy)e^{-y}+C(y)$ 又因为题干中给的条件$f(u,0)=u^2{e}^{-u}$,所以我们得想办法用上这个条件。 令$y=x$，则f(x,y-x)=f(x,0)。
所以$C(x)=x^2{e}^{-x}$, 所以$C(y)=y^2{e}^{-y}$所以$g(x,y)=2(x^2-xy)e^{-y}+y^2{e}^{-y}$；所以$f(x,y-x)=2(x^2-xy)e^{-y}+y^2{e}^{-y}$ ,而本题让我们求的是$f(u,v)$,所以我们不妨令$u=x,v=y-x$则$x=u,y=u+v$;
所以$f(u,v)=2[u^2-u(u+v)]e^{-(u+v)}+(u+v{)}^2{e}^{-(u+v)}=-2uv{e}^{-(u+v)}+(u+v{)}^2{e}^{-(u+v)}=(u^2+v^2)e^{-(u+v)}$;
知道了$f(u,v)=(u^2+v^2)e^{-(u+v)}$,让我们求极值，我们就来算下驻点
$$\{\begin{array}{l}\frac{\partial f(u,v)}{\partial u}=2u{e}^{-(u+v)}-(u^2+v^2)e^{-(u+v)}=0,\\ \frac{\partial f(u,v)}{\partial v}=2v{e}^{-(u+v)}-(u^2+v^2)e^{-(u+v)}=0,\end{array}$$
解得$\{\begin{array}{l}u=0,\\ v=0\end{array}$或者$\{\begin{array}{l}u=1,\\ v=1\end{array}$
而$$\frac{{\partial }^{2}f}{\partial u^2}=(2-2u)e^{-(u+v)}-(2u-u^2-v^2)e^{-(u+v)},$$
$$\frac{{\partial }^{2}f}{\partial v^2}=(2-2v)e^{-(u+v)}-(2v-u^2-v^2)e^{-(u+v)},$$
$$\frac{{\partial }^{2}f}{\partial u\partial v}=-2v{e}^{-(u+v)}-(2u-u^2-v^2)e^{-(u+v)},$$
当$\{\begin{array}{l}u=0,\\ v=0\end{array}$ 时， $A=2，C=2，B=0,AC-B^2>0$，且A>0,所以有极小值$f(0,0)=0$。
当$\{\begin{array}{l}u=1,\\ v=1\end{array}$时，$A=2,C=0,B=-2e^{-2},AC-B^2<0$,所以$f(1,1)$不是极值。

下面我们回顾下多元函数求极值的知识点如下：

思路分析：

看到要证明积分不等式的问题，首先想到构造函数，那构造什么样的函数呢？题目要证明什么，我们就构造什么,本题我们就可以构造$F(x)=(x-a)f(\frac{a+x}{2})-{\int }_a^{x}f(t)dt$

证明：

必要性： 令$F(x)=(x-a)f(\frac{a+x}{2})-{\int }_a^{x}f(t)dt$ ，很明显F(a)=0,
$F^{\prime }(x)=f(\frac{a+x}{2})+\frac{1}{2}(x-a)f^{\prime }(\frac{a+x}{2})-f(x)$
$$=\frac{1}{2}(x-a)\acute{f}(\frac{a+x}{2})-[f(x)-f(\frac{a+x}{2})]$$$$=\frac{1}{2}(x-a)f^{\prime }(\frac{a+x}{2})-\frac{1}{2}(x-a)\acute{f(\xi )}$$,$\xi \in (\frac{a+x}{2},x)$$$=\frac{1}{2}(x-a)[\acute{f}(\frac{a+x}{2})-f^{\prime }(\xi ))]$$
因为$f^{\prime \prime }(x)>0,f^{\prime }(\frac{a+x}{2})-f^{\prime }(\xi )<0$,故而 $F^{\prime }(x)<0$, 所以$F(b)\le F(a)=0$,所以$F(b)=(b-a)f(\frac{a+b}{2})-{\int }_a^{b}f(t)dt\le 0,即f(\frac{a+b}{2})<\frac{1}{b-a}{\int }_a^{b}f(t)dt$

充分性：
$\forall x_0\in (-\infty ,+\infty )$,取$a=x_0-h,b=x_0+h$,其中$h>0$,那我们的式子$f(\frac{a+b}{2})\le \frac{1}{b-a}{\int }_a^{b}f(t)dt$就可以转化成$f(x_0)\le \frac{1}{2h}{\int }_{x_0-h}^{x_0+h}f(x)dx\iff \frac{{\int }_{x_0-h}^{x_0+h}f(x)dx-2hf(x_0)}{2h}\ge 0$,

为了证明题目中的$f^{\prime \prime }(x)\ge 0,$我们只能想到2种办法
①从导数的定义式上入手，想办法构造导数的定义式
②利用泰勒公式(因为泰勒公式里面还有一阶导和二阶导)
③洛必达法则（不停地分子分母洛下去，必定能出现高阶导数）
对于本题而言，我们已经引入了邻域$(x_0-h,x_0+h)$,因为要证明$f^{\prime \prime }(x)$,所以我们不妨假设a和b隔得非常非常近，即${\lim }_{h\to 0}$，对于这种求极限的情况，我们首先想到洛必达法则，故而对于式子$\frac{{\int }_{x_0-h}^{x_0+h}f(x)dx-2hf(x_0)}{2h}\ge 0$,我们可以想办法用洛必达法则解决，对于分子而言，必须要进行3次求导才能出现$f^{\prime \prime }(x)$二阶导，而分母却经不起3次求导，那怎么办呢，我们把分母的次幂加大到3阶$\frac{{\int }_{x_0-h}^{x_0+h}f(x)dx-2hf(x_0)}{2h^3}\ge 0$,然后上下求导
${\lim }_{h\to 0}\frac{{\int }_{x_0-h}^{x_0+h}f(x)dx-2hf(x_0)}{2h^3}$
$$=\underset{h\to 0}{\lim }\frac{f(x_0+h)-f(x_0-h)-2f(x_0)}{6h^2}$$$$=\underset{h\to 0}{\lim }\frac{f^{\prime }(x_0+h)+f^{\prime }(x_0-h)}{12h}$$$$=\underset{h\to 0}{\lim }\frac{f^{\prime \prime }(x_0+h)-f^{\prime \prime }(x_0-h)}{12}$$
当$h\to 0$时，分子就是$f^{\prime \prime }(x_0)+f^{\prime \prime }(x_0)=2f^{\prime \prime }(x_0)$
所以$$=\underset{h\to 0}{\lim }\frac{f^{\prime \prime }(x_0+h)+f^{\prime \prime }(x_0-h)}{12}=\frac{f^{\prime \prime }(x_0)}{6}$$
所以$\frac{f^{\prime \prime }(x_0)}{6}\ge 0$，由极限保号性，$f^{\prime \prime }(x_0)\ge 0$. 本题得证

解:(1) 第一问出的很常规，无非就是让你求矩阵的特征值，然后计算对应特征值的特征向量，然后把特征向量单位化，正交化就完事了

（2）通常来说，第二问一般会用到第一问的结论
所以${\min }_{x\to 0}\frac{f(x_1,x_2,x_3)}{x^{T}x}=\frac{4y_1^2+4y_2^2+2y_3^2}{y_1^2+y_2^2+y_3^2}=2+\frac{2y_1^2+2y_2^2}{y_1^2+y_2^2+y_3^2}$ ,当$y_1=y_2=0$时，取最小值是2。
回答完毕。