第一课: 随机过程简介

第一课 : 随机过程简介

一、基本概念

Q1:什么是随机过程？

在介绍什么是随机过程之前，先了解下述两个概念:

【随机】的【不是过程】的是什么东西？
答案是【随机变量】： $X(\omega ):\Omega \to \mathcal{R}$
随机变量就是将 样本空间映射到实数域上的一个映射.

【不随机】的【过程】是什么？
答案是【函数】：$f(t):T\to \mathcal{R}$ .
函数可以将一段时间按照一定规则确定的映射成一个实数.

而我们要介绍的随机过程其实就是同时兼具 随机性与 过程 性的映射 :

【随机过程】: 同一概率空间上的一族随机变量

数学形式: X = { X ( t , ω ) : t ∈ T , ω ∈ Ω } X= \{X(t,\omega):t \in T,\omega \in \Omega\} X={ X(t,ω):t∈T,ω∈Ω}
也常简写成 : { X t ( ω ) : t ∈ T , ω ∈ Ω } \{X_t(\omega):t\in T,\omega \in \Omega \} { Xt​(ω):t∈T,ω∈Ω} 或 { X ( t ) : t ∈ T } \{X(t):t \in T\} { X(t):t∈T}

以映射视角看待 : $X(t,\omega ):T\times \Omega \to \mathcal{S}$
其中 $T:指标集；\Omega ：样本空间；\mathcal{S}：状态空间$

• 给定 $t$ 和 $\omega$ , $X(t,\omega )$ 是确定的数
• 给定 $t$ 时， $X(t,.)$ 是随机变量
• 给定$\omega$ 时 , $X(.,\omega )$ 是 随机过程的一条轨道

图形化理解(参考出处)：

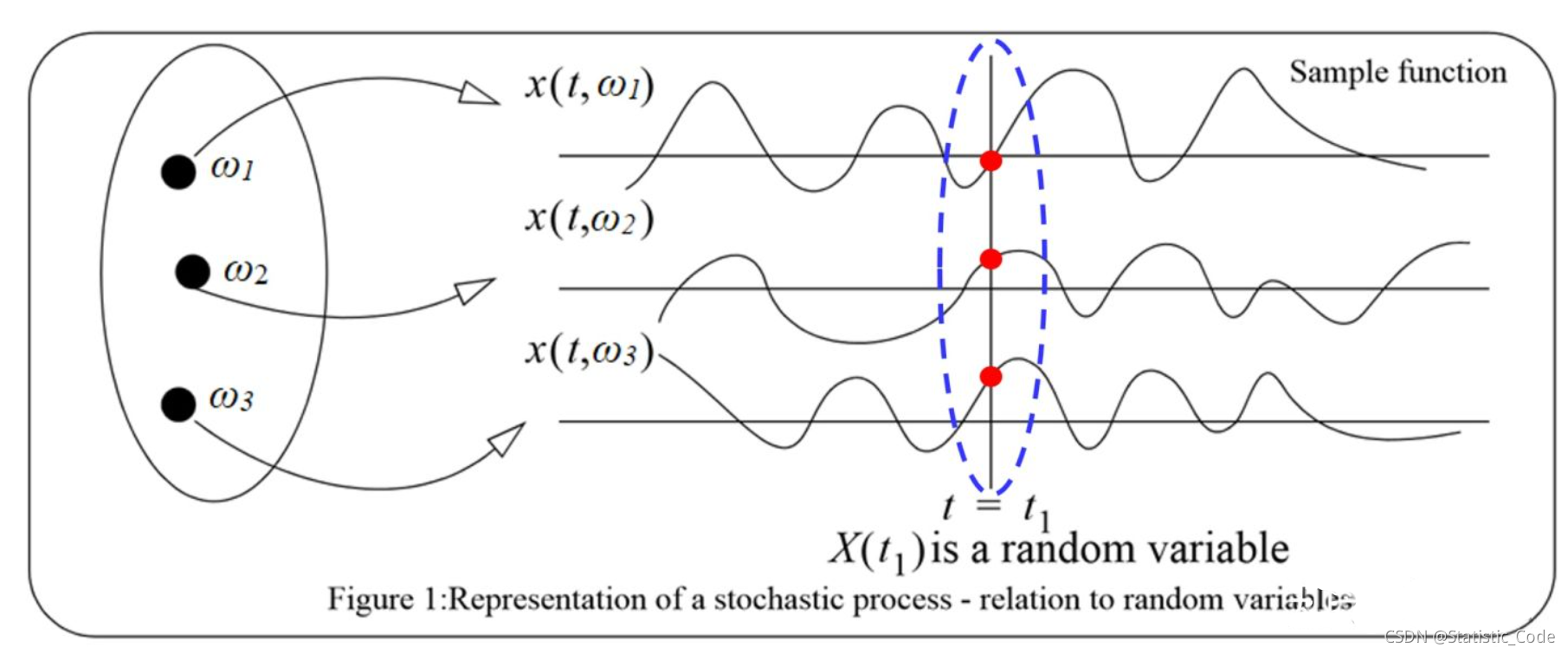
图中的三条样本函数曲线可分别看成是三个粒子的位移时间图像，每个粒子在 $t$ 时刻的位置均为时间 $t$ 的函数。所有粒子在 $t$ 时刻的空间位置（图中红点）就是随机变量在 $t$ 时刻的状态。因此，随机过程既可看成是“所有随机变量的集合”，也可看成为“所有样本轨道的集合”，而样本轨道只是随机过程集合中的一个元素。

个人理解 ： 随机过程就是既有时间维度也有随机属性的二元映射，"横着"看 对于给定样本点${\omega }_0$, $X(t,{\omega }_0)$ 就是时间$t$的函数曲线 ；"竖着"看 对于给定的时间点$t_0$ ，$X(\omega ,t_0)$ 就是一个随机变量.

举例: 公交站某天每时每刻等车的人数.

注1 上述对随机过程的定义限定了每个时刻$t$处的随机变量是在同一个概率空间上取值的，其实这是为了后续分析简便，严格来讲完全可以取不同的概率空间。

---

Q2:随机过程的刻画

随机过程是用有限维分布族刻画的.

定义【有限维分布族】
设 X = { X t : t ∈ T } X=\{X_t:t \in T\} X={ Xt​:t∈T} 是随机过程, 我们称函数族 { F t 1 , . . . , t k ( x 1 , . . . , x k ) : t 1 , . . . , t k ∈ T , k ∈ Z + } \{F_{t_1,...,t_k}(x_1,...,x_k):t_1,...,t_k \in T ,k \in \mathcal{Z}^+ \} { Ft1​,...,tk​​(x1​,...,xk​):t1​,...,tk​∈T,k∈Z+